Es wird verstanden von Invers multiplikativ von einer Zahl ergibt eine andere Zahl, die mit der ersten multipliziert wird, als Ergebnis das neutrale Element des Produkts, dh die Einheit. Wenn Sie eine reelle Zahl haben zu dann wird seine multiplikative Inverse mit bezeichnet zu-1, und es ist wahr, dass:
a a-1 = a-1 a = 1
Normalerweise die Nummer zu gehört zu einer Menge von reellen Zahlen.
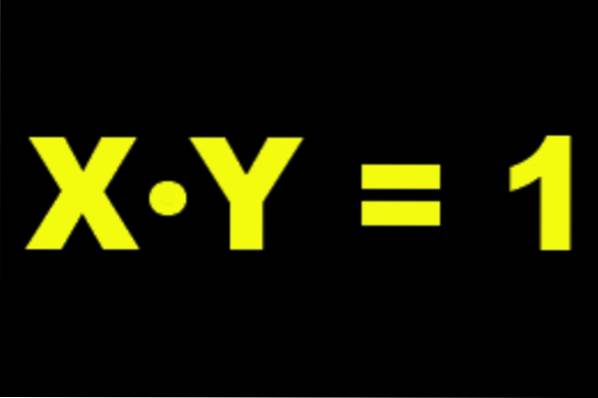
Wenn wir zum Beispiel nehmen a = 2, dann ist seine multiplikative Inverse zwei-1 = ½ da folgendes überprüft wird:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Zum Invers multiplikativ einer Zahl wird auch die genannt wechselseitig, da die multiplikative Inverse durch Austausch von Zähler und Nenner erhalten wird, beträgt beispielsweise die multiplikative Inverse von 3/4 4/3.
Generell kann gesagt werden, dass für eine rationale Zahl (p / q) seine multiplikative Inverse (p / q)-1 Es ist wechselseitig (q / p) wie unten überprüft werden kann:
(p / q) ⋅ (p / q)-1 = (p / q) ⋅ (q / p) = (p⋅ q) / (q⋅ p) = (p⋅ q) / (p⋅ q) = 1
Die multiplikative Inverse existiert nicht in der numerischen Menge von ganzen Zahlen, Wenn zum Beispiel die ganze Zahl 2 genommen wird, wäre ihre multiplikative Inverse gemäß dem, was oben gesehen wurde, ½, aber eine ½ ist keine ganze Zahl..
Es gibt auch keine multiplikative Umkehrung des Nullelements der Multiplikation. Mit anderen Worten, die Zahl Null (0), die das Nullelement der Multiplikationsoperation ist, hat keine multiplikative Inverse, da es keine Zahl gibt, die mit der Einheit Null multipliziert wird.
Die multiplikative Inverse existiert in rationalen Zahlen, in reellen Zahlen und in komplexen Zahlen.
Finden Sie die multiplikative Inverse von 3/2 und stellen Sie sicher, dass sie die Eigenschaft multiplikativer Ganzzahlen erfüllt.
Gemäß der oben angegebenen Regel werden Zähler und Nenner auf diese Weise vertauscht. Die multiplikative Inverse von (3/2) ist (2/3). Um die Multiplikation der beiden Zahlen zu überprüfen, wird Folgendes durchgeführt:
(3/2) ≤ (2/3) = (3 ≤ 2) / (2 ≤ 3) = 6/6 = 1.
Um zwei Bruchzahlen zu multiplizieren, multiplizieren Sie einfach den Zähler der ersten mit dem Zähler der zweiten, um den Zähler des Ergebnisses zu erhalten..
Um den Nenner eines Produkts mit Bruchzahlen zu erhalten, gehen Sie auf ähnliche Weise vor, dh multiplizieren Sie die Nenner miteinander, und das Ergebnis ist der Nenner des Produkts. In unserem Beispiel wird überprüft, dass der Zähler des Produkts der Zahl und seines Kehrwerts 6 und der Nenner 6 ist, wobei der Bruch 6/6 übrig bleibt, der 1 ist.
Die multiplikative Inverse von -5 sollte nicht mit ihrer Symmetrie (+5) verwechselt werden, die manchmal als arithmetische Inverse bezeichnet wird. Die multiplikative Inverse wird wie folgt erhalten:
(-5) ⋅ X = 1
Wobei X die zu erhaltende multiplikative Inverse ist. Eine mögliche Prozedur besteht darin, nach dem unbekannten X zu lösen. Da (-5) das unbekannte X im linken Element multipliziert, wird das rechte Element geteilt:
X = 1 / (-5)
Da bekannt ist, dass + zwischen - ist -, wird schließlich X erhalten:
X = - ⅕ .
Zusammenfassend ist - ⅕ die multiplikative Inverse von -5.
Erhalten Sie die multiplikative Inverse von -√2. Angenommen, die multiplikative Inverse ist X, dann muss -√2 multipliziert mit X Eins sein, eine Bedingung, die wir unten auferlegen:
-√2 ⋅ X = 1
Als nächstes werden beide Mitglieder durch -√2 geteilt, um Folgendes zu erhalten:
(-√2 ⋅ X) / (-√2) = 1 / (-√2)
Im ersten Mitglied wird -√2 vereinfacht, so dass:
X = 1 / (-√2)
Dieser Ausdruck kann rationalisiert werden, dh die Wurzel des Nenners wird eliminiert, indem im Zähler mit (-√2) und im Nenner mit demselben Betrag multipliziert wird, damit das Ergebnis nicht geändert wird:
X = (-√2) / [(-√2) (- √2)] = - (√2 / 2)
Zusammenfassend ist - (√2 / 2) die multiplikative Inverse von (-√2).
Nehmen wir eine beliebige Zahl x an, erhalten Sie ihre multiplikative Inverse und stellen Sie sie grafisch dar.
In diesem Fall ist es eine Funktion f (x) = x. Um die multiplikative Inverse zu erhalten, muss die Funktion g (x) so gefunden werden, dass sie mit der ersten Zahl der Einheit multipliziert wird. Die Funktion g ist der Kehrwert von f und sollte in keiner Weise mit ihrer Umkehrfunktion verwechselt werden.
Mit anderen Worten, die multiplikative Inverse von x ist ein y, so dass Folgendes zutrifft:
x ⋅ y = 1
von wo Clearing und Sie haben:
y = 1 / x.
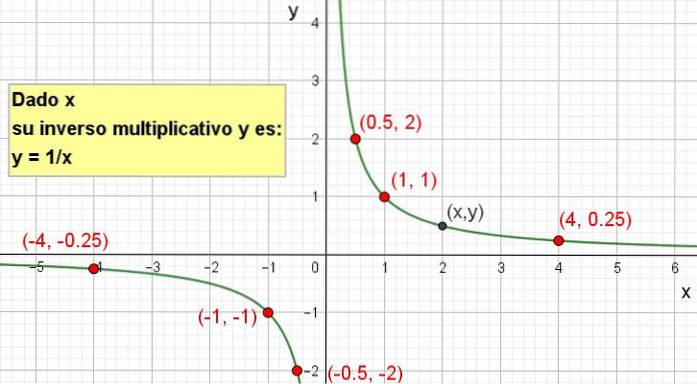
Das Obige wird so interpretiert, dass ein Wert von x gegeben ist. Die vorherige Formel gibt uns die multiplikative Inverse.
Es ist möglich, die grafische Darstellung wie in der folgenden Abbildung dargestellt zu erstellen:
Wenn x = 2 - √2 ist, erhalten Sie das multiplikative Inverse y.
Lösung:
Damit y eine multiplikative Inverse von x ist, muss die folgende Gleichheit erfüllt sein:
x ⋅ y = 1
Ersetzen Sie x durch seinen Wert:
(2 - √2) ⋅ y = 1
Dann klärt es und:
y = 1 / (2 - √2)
Um das Ergebnis zu rationalisieren, werden Zähler und Nenner mit ihrem konjugierten Binom multipliziert:
y = (2 + √2) / ((2 + √2) (2 - √2))
Im Nenner wird ein bemerkenswertes Produkt erkannt, das als Produkt einer Summe und einer Differenz bezeichnet wird, dh der Differenz der Quadrate. Auf diese Weise verschwindet die Wurzel im Nenner.
y = (2 + √2) / (2 ^ 2 - (√2) ^ 2)
Lösen der Kräfte:
y = (2 + √2) / (4 - 2)
Vereinfachung:
y = (2 + √2) / 2
Erhalten Sie die multiplikative Inverse von (1 / a + 1 / b), wobei a und b reelle Zahlen ungleich Null sind.
Lösung:
Wir nennen Y die multiplikative Inverse von (1 / a + 1 / b), daher muss die folgende Gleichung erfüllt sein:
Und ⋅ (1 / a + 1 / b) = 1
Die Variable Y wird gelöscht:
Y = 1 / (1 / a + 1 / b)
Der Nenner ist gelöst:
Y = 1 / ((b + a) / a b)
Wie aus den Regeln der Algebra bekannt ist, geht der Nenner des Nenners auf den Zähler über:
Y = (a b) / (b + a)
Es wird befohlen, endlich zu erhalten:
(a b) / (a + b), welches die multiplikative Inverse von (1 / a + 1 / b) ist.
Erhalten Sie die multiplikative Inverse von (a - b) / (a ^ 2 - b ^ 2).
Lösung:
Denken Sie daran, dass die multiplikative Inverse auch als Kehrwert bezeichnet wird, da sie genau durch Austausch von Zähler und Nenner erhalten wird.
Dann ist die multiplikative Inverse von (a - b) / (a ^ 2 - b ^ 2):
(a ^ 2 - b ^ 2) / (a - b)
Dieser Ausdruck kann jedoch vereinfacht werden, wenn wir nach den Regeln der Algebra erkennen, dass der Zähler eine Differenz von Quadraten ist, die als Produkt einer Summe durch eine Differenz berücksichtigt werden kann:
((a + b) (a - b)) / (a - b)
Da es im Zähler und im Nenner einen gemeinsamen Faktor (a - b) gibt, vereinfachen wir ihn und erhalten schließlich:
(a + b) ist die multiplikative Inverse von (a - b) / (a ^ 2 - b ^ 2).
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.