Magnetische Induktionsformeln, wie sie berechnet werden und Beispiele

Das magnetische Induktion oder die magnetische Flussdichte ist eine Veränderung der Umgebung, die durch das Vorhandensein elektrischer Ströme verursacht wird. Sie verändern die Art des sie umgebenden Raums und schaffen eine Landschaft Vektor.

Der Vektor magnetische Induktion, magnetische Flussdichte Oder einfach Magnetfeld B., Es hat drei charakteristische Merkmale: eine Intensität, die durch einen numerischen Wert ausgedrückt wird, eine Richtung und auch einen Sinn, der an jedem Punkt im Raum gegeben ist. Es ist fett hervorgehoben, um es von rein numerischen oder skalaren Größen zu unterscheiden.

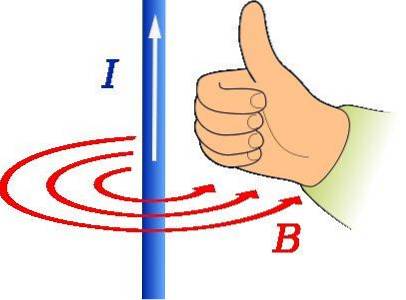
Die rechte Daumenregel wird verwendet, um die Richtung und Richtung des Magnetfelds zu ermitteln, das durch einen stromführenden Draht verursacht wird, wie in der obigen Abbildung gezeigt.

Der Daumen der rechten Hand sollte in Stromrichtung zeigen. Dann zeigt die Drehung der vier verbleibenden Finger die Form von an B., was in der Figur durch die konzentrischen roten Kreise dargestellt ist.

In einem solchen Fall ist die Adresse von B. ist tangential zum Umfang konzentrisch zum Draht und gegen den Uhrzeigersinn.

Das magnetische Induktion B. Im internationalen System wird Tesla (T) gemessen, es wird jedoch häufiger in einer anderen Einheit namens Gauß (G) gemessen. Beide Einheiten wurden jeweils zu Ehren von Nikola Tesla (1856-1943) und Carl Friedrich Gauss (1777-1855) für ihre außergewöhnlichen Beiträge zur Wissenschaft von Elektrizität und Magnetismus benannt..

Artikelverzeichnis

• 1 Was sind die Eigenschaften der magnetischen Induktion oder der magnetischen Flussdichte??
• 2 Biot-Savarts Gesetz
• 3 Formeln
• 4 Wie wird es berechnet??
  • 4.1 Beispiel
• 5 Referenzen

Was sind die Eigenschaften der magnetischen Induktion oder der magnetischen Flussdichte??

Ein Kompass, der sich in der Nähe eines stromführenden Kabels befindet, wird immer mit ausgerichtet B.. Der dänische Physiker Hans Christian Oersted (1777-1851) war der erste, der dieses Phänomen im frühen 19. Jahrhundert bemerkte.

Und wenn die Strömung aufhört, zeigt der Kompass wie immer wieder in den geografischen Norden. Durch sorgfältiges Ändern der Position des Kompasses wird eine Karte der Form des Magnetfelds erhalten.

Diese Karte hat immer die Form von Kreisen, die konzentrisch zum Draht sind, wie zu Beginn beschrieben. Auf diese Weise können Sie visualisieren B..

Auch wenn der Draht nicht gerade ist, der Vektor B. es wird konzentrische Kreise um ihn herum bilden. Stellen Sie sich zur Bestimmung der Feldform nur sehr kleine Drahtsegmente vor, die so klein sind, dass sie geradlinig erscheinen und von konzentrischen Kreisen umgeben sind..

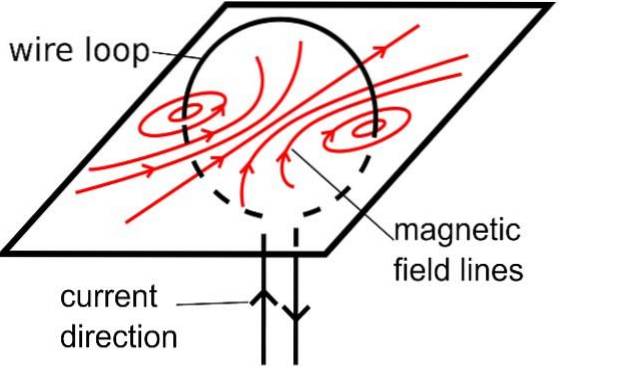
Dies weist auf eine wichtige Eigenschaft von Magnetfeldlinien hin. B.: Sie haben keinen Anfang oder Ende, sie sind immer geschlossene Kurven.

Biot-Savarts Gesetz

Das 19. Jahrhundert war der Beginn des Zeitalters der Elektrizität und des Magnetismus in der Wissenschaft. Um das Jahr 1820 entdeckten die französischen Physiker Jean Marie Biot (1774-1862) und Felix Savart (1791-1841) das Gesetz, das ihren Namen trägt und das es uns ermöglicht, den Vektor zu berechnen B..

Sie machten die folgenden Beobachtungen über den Beitrag zu dem Magnetfeld, der von einem Drahtsegment unterschiedlicher Länge erzeugt wird dl das führt einen elektrischen Strom ich::

• Die Größe von B. nimmt mit dem umgekehrten Quadrat des Abstands zum Draht ab (dies ist sinnvoll: vom Draht weg die Intensität von B. muss kleiner sein als nahe Punkte).
• Die Größe von B. ist proportional zur Stromstärke ich das geht durch den Draht.
• Die Adresse von B. ist tangential zum Radiusumfang r zentriert auf dem Draht und dem Sinn von B. wird, wie gesagt, durch die Regel des rechten Daumens gegeben.

Das Kreuzprodukt oder Kreuzprodukt ist das geeignete mathematische Werkzeug, um den letzten Punkt auszudrücken. Um ein Vektorprodukt zu etablieren, werden zwei Vektoren benötigt, die wie folgt definiert sind:

• dl ist der Vektor, dessen Größe die Länge des Differentialsegments ist dl
• r ist der Vektor, der vom Draht zu dem Punkt geht, an dem Sie das Feld finden möchten

Formeln

All dies kann zu einem mathematischen Ausdruck kombiniert werden:

Die zur Herstellung der Gleichheit erforderliche Verhältnismäßigkeitskonstante ist die magnetische Permeabilität des freien Raums μ_oder  = 4π.10^-7 T.m / A.

Dieser Ausdruck ist das Biot- und Savart-Gesetz, mit dem wir das Magnetfeld eines Stromsegments berechnen können.

Ein solches Segment muss wiederum Teil eines größeren und geschlosseneren Kreislaufs sein: einer Stromverteilung.

Die Bedingung, dass der Stromkreis geschlossen ist, ist erforderlich, damit elektrischer Strom fließt. In offenen Stromkreisen kann kein elektrischer Strom fließen.

Um schließlich das Gesamtmagnetfeld dieser Stromverteilung zu ermitteln, werden alle Beiträge jedes Differenzsegments addiert dl. Dies entspricht einer Integration über die gesamte Distribution:

Um das Biot-Savart-Gesetz anzuwenden und den magnetischen Induktionsvektor zu berechnen, müssen einige sehr wichtige wichtige Punkte berücksichtigt werden:

• Das Kreuzprodukt zwischen zwei Vektoren führt immer zu einem anderen Vektor.

• 

• Es ist bequem, das Vektorprodukt zu finden Vor Um zur Auflösung des Integrals überzugehen, wird das Integral jeder der separat erhaltenen Komponenten gelöst.
• Es ist notwendig, ein Bild der Situation zu zeichnen und ein geeignetes Koordinatensystem zu erstellen.
• Wann immer das Vorhandensein einer gewissen Symmetrie beobachtet wird, sollte diese verwendet werden, um Rechenzeit zu sparen.
• Wenn es Dreiecke gibt, sind der Satz von Pythagoras und der Satz von Cosinus eine große Hilfe, um die geometrische Beziehung zwischen den Variablen herzustellen.

Wie wird es berechnet??

Mit einem praktischen Beispiel für die Berechnung von B. Für einen geraden Draht gelten diese Empfehlungen.

Beispiel

Berechnen Sie den Magnetfeldvektor, den ein sehr langer geradliniger Draht an einem Punkt P im Raum erzeugt, gemäß der gezeigten Abbildung.

Aus der Figur muss man:

• Der Draht ist in vertikaler Richtung gerichtet, wobei der Strom I nach oben fließt. Diese Richtung ist + y im Koordinatensystem, dessen Ursprung am Punkt O liegt.

• 

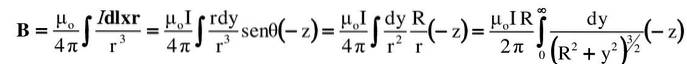
• In einem solchen Fall nach der Regel des rechten Daumens, B. am Punkt P ist es auf die Innenseite des Papiers gerichtet, weshalb es in der Figur durch einen kleinen Kreis und ein „x“ gekennzeichnet ist. Diese Adresse wird als -z angenommen.
• Das rechte Dreieck, dessen Beine sind Y. Y. R., beziehen beide Variablen nach dem Satz von Pythagoras in Beziehung: r^zwei= R.^zwei+Y.^zwei

All dies wird im Integral ersetzt. Das Kreuzprodukt oder Kreuz wird durch seine Größe plus seine Richtung und seinen Sinn angezeigt:

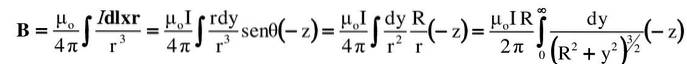
Das vorgeschlagene Integral befindet sich in einer Tabelle von Integralen oder wird durch eine geeignete trigonometrische Substitution gelöst (der Leser kann das Ergebnis mit überprüfen y = Rtg & thgr;)::

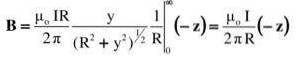
Das Ergebnis stimmt mit dem überein, was erwartet wurde: Die Größe des Feldes nimmt mit dem Abstand R ab und nimmt proportional mit der Intensität des Stroms I zu.

Obwohl ein unendlich langer Draht eine Idealisierung ist, ist der erhaltene Ausdruck eine sehr gute Annäherung für das Feld eines langen Drahtes.

Mit dem Gesetz von Biot und Savart ist es möglich, das Magnetfeld anderer hochsymmetrischer Verteilungen zu finden, beispielsweise einer kreisförmigen Schleife, die Strom führt, oder gebogener Drähte, die geradlinige und krummlinige Segmente kombinieren..

Um das vorgeschlagene Integral analytisch zu lösen, muss das Problem natürlich einen hohen Grad an Symmetrie aufweisen. Andernfalls besteht die Alternative darin, das Integral numerisch zu lösen.

Verweise

1. Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 2. Mexiko. Cengage Learning Editors. 367-372.