
Mögliche Gradientenmerkmale, Berechnung und Beispiel

Das potentieller Gradient ist ein Vektor, der die Änderungsrate des elektrischen Potentials in Bezug auf den Abstand in jeder Achse eines kartesischen Koordinatensystems darstellt. Somit gibt der Potentialgradientenvektor die Richtung an, in der die Änderungsrate des elektrischen Potentials in Abhängigkeit von der Entfernung größer ist.
Der Modul des Potentialgradienten spiegelt wiederum die Änderungsrate der Änderung des elektrischen Potentials in einer bestimmten Richtung wider. Wenn der Wert davon an jedem Punkt eines räumlichen Bereichs bekannt ist, kann das elektrische Feld aus dem Potentialgradienten erhalten werden.

Das elektrische Feld ist als Vektor definiert und hat daher eine bestimmte Richtung und Größe. Durch Bestimmen der Richtung, in der das elektrische Potential am schnellsten abnimmt - weg vom Referenzpunkt - und Teilen dieses Wertes durch die zurückgelegte Strecke wird die Größe des elektrischen Feldes erhalten.
Artikelverzeichnis
- 1 Funktionen
- 2 Wie berechnet man es??
- 3 Beispiel
- 3.1 Übung
- 4 Referenzen
Eigenschaften
Der Potentialgradient ist ein durch bestimmte Raumkoordinaten begrenzter Vektor, der das Änderungsverhältnis zwischen dem elektrischen Potential und der von diesem Potential zurückgelegten Strecke misst.
Die herausragendsten Eigenschaften des elektrischen Potentialgradienten sind nachstehend aufgeführt:
1- Der Potentialgradient ist ein Vektor. Daher hat es eine bestimmte Größe und Richtung.
2- Da der Potentialgradient ein Vektor im Raum ist, hat er Größen, die auf die X- (Breite), Y- (Höhe) und Z- (Tiefe) Achse gerichtet sind, wenn das kartesische Koordinatensystem als Referenz genommen wird.
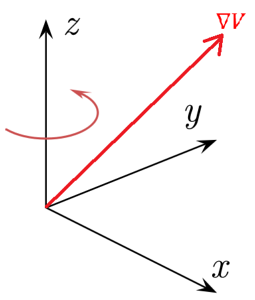
3- Dieser Vektor steht senkrecht zur Äquipotentialfläche an dem Punkt, an dem das elektrische Potential ausgewertet wird.
4- Der Potentialgradientenvektor ist an jedem Punkt auf die Richtung der maximalen Variation der elektrischen Potentialfunktion gerichtet.
5- Der Modul des Potentialgradienten ist gleich der Ableitung der elektrischen Potentialfunktion in Bezug auf die zurückgelegte Strecke in Richtung jeder der Achsen des kartesischen Koordinatensystems.
6- Der Potentialgradient hat an stationären Punkten (Maxima, Minima und Sattelpunkte) den Wert Null..
7- Im internationalen Einheitensystem (SI) sind die Maßeinheiten des Potentialgradienten Volt / Meter.
8- Die Richtung des elektrischen Feldes ist dieselbe, in der das elektrische Potential seine Größe schneller verringert. Der Potentialgradient zeigt wiederum in die Richtung, in die das Potential im Verhältnis zu einer Positionsänderung an Wert zunimmt. Das elektrische Feld hat also den gleichen Wert des Potentialgradienten, jedoch mit dem entgegengesetzten Vorzeichen.
Wie man es berechnet?
Die Differenz des elektrischen Potentials zwischen zwei Punkten (Punkt 1 und Punkt 2) ergibt sich aus folgendem Ausdruck:
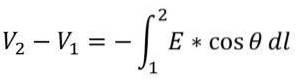
Wo:
V1: elektrisches Potential an Punkt 1.
V2: elektrisches Potential an Punkt 2.
E: Stärke des elektrischen Feldes.
Ѳ: Winkel der Neigung des gemessenen elektrischen Feldvektors in Bezug auf das Koordinatensystem.
Wenn diese Formel differenziell ausgedrückt wird, gilt Folgendes:
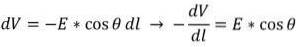
Der Faktor E * cos (Ѳ) bezieht sich auf den Modul der elektrischen Feldkomponente in Richtung von dl. Sei L die horizontale Achse der Referenzebene, dann ist cos (Ѳ) = 1 wie folgt:
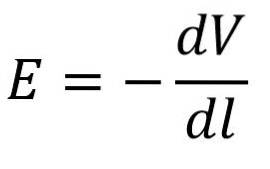
Nachfolgend ist der Quotient zwischen der Änderung des elektrischen Potentials (dV) und der Änderung der zurückgelegten Strecke (ds) der Modul des Potentialgradienten für die Komponente.
Daraus folgt, dass die Größe des elektrischen Potentialgradienten gleich der Komponente des elektrischen Feldes in Untersuchungsrichtung ist, jedoch mit dem entgegengesetzten Vorzeichen.
Da die reale Umgebung jedoch dreidimensional ist, muss der potenzielle Gradient an einem bestimmten Punkt als die Summe von drei räumlichen Komponenten auf der X-, Y- und Z-Achse des kartesischen Systems ausgedrückt werden..
Indem wir den elektrischen Feldvektor in seine drei rechteckigen Komponenten zerlegen, haben wir Folgendes:
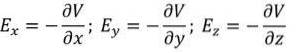
Wenn es in der Ebene einen Bereich gibt, in dem das elektrische Potential den gleichen Wert hat, ist die partielle Ableitung dieses Parameters in Bezug auf jede der kartesischen Koordinaten Null.
An Punkten, die sich auf Äquipotentialflächen befinden, hat die Intensität des elektrischen Feldes somit eine Größe von Null.
Schließlich kann der Potentialgradientenvektor als genau der gleiche elektrische Feldvektor (in der Größe) mit dem entgegengesetzten Vorzeichen definiert werden. Somit haben wir folgendes:
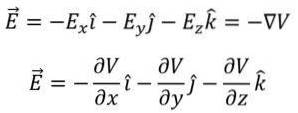
Beispiel
Aus den vorherigen Berechnungen ist Folgendes erforderlich:
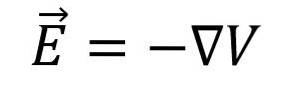
Bevor nun das elektrische Feld als Funktion des Potentialgradienten oder umgekehrt bestimmt wird, muss zunächst bestimmt werden, in welche Richtung die elektrische Potentialdifferenz wächst.
Danach wird der Quotient aus der Änderung des elektrischen Potentials und der Änderung der zurückgelegten Nettodistanz bestimmt.
Auf diese Weise wird die Größe des zugehörigen elektrischen Feldes erhalten, die gleich der Größe des Potentialgradienten in dieser Koordinate ist.
Übung
Es gibt zwei parallele Platten, wie in der folgenden Abbildung dargestellt.
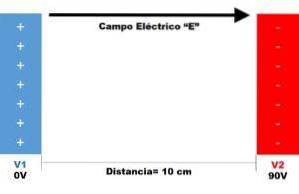
Schritt 1
Die Wachstumsrichtung des elektrischen Feldes wird am kartesischen Koordinatensystem bestimmt.
Das elektrische Feld wächst aufgrund der Anordnung der parallelen Platten nur in horizontaler Richtung. Folglich ist es möglich zu schließen, dass die Komponenten des Potentialgradienten in der Y-Achse und der Z-Achse Null sind..
Schritt 2
Daten von Interesse werden diskriminiert.
- Potentialdifferenz: dV = V2 - V1 = 90 V - 0 V => dV = 90 V..
- Abstandsunterschied: dx = 10 Zentimeter.
Um die Konsistenz der nach dem Internationalen Einheitensystem verwendeten Maßeinheiten zu gewährleisten, müssen die nicht in SI ausgedrückten Mengen entsprechend umgerechnet werden. 10 Zentimeter entsprechen also 0,1 Metern und schließlich: dx = 0,1 m.
Schritt 3
Berechnen Sie die Größe des potenziellen Gradientenvektors entsprechend.
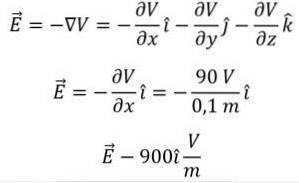
Verweise
- Elektrizität (1998). Encyclopædia Britannica, Inc. London, Großbritannien. Wiederhergestellt von: britannica.com
- Potentieller Gradient (s.f.). Nationale Autonome Universität von Mexiko. Mexiko DF, Mexiko. Wiederhergestellt von: professors.dcb.unam.mx
- Elektrische Wechselwirkung. Wiederhergestellt von: matematicasypoesia.com.es
- Potentieller Gradient (s.f.). Wiederhergestellt von: Circuitglobe.com
- Beziehung zwischen Potential und elektrischem Feld (s.f.). Technologisches Institut von Costa Rica. Cartago, Costa Rica. Wiederhergestellt von: repositoriotec.tec.ac.cr
- Wikipedia, die freie Enzyklopädie (2018). Gradient. Wiederhergestellt von: es.wikipedia.org



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.