Das euklidische Geometrie entspricht der Untersuchung der Eigenschaften geometrischer Räume, in denen Euklids Axiome erfüllt sind. Obwohl dieser Begriff manchmal verwendet wird, um Geometrien mit höheren Abmessungen und ähnlichen Eigenschaften abzudecken, ist er im Allgemeinen gleichbedeutend mit klassischer Geometrie oder ebener Geometrie..
Im III Jahrhundert a. C. Euklid und seine Schüler schrieben das Elemente, eine Arbeit, die das mathematische Wissen der Zeit umfasste und mit einer logisch-deduktiven Struktur ausgestattet war. Seitdem wurde Geometrie eine Wissenschaft, zunächst um klassische Probleme zu lösen, und entwickelte sich zu einer prägenden Wissenschaft, die zur Vernunft beiträgt..
Artikelverzeichnis
Um über die Geschichte der euklidischen Geometrie zu sprechen, ist es wichtig, mit Euklid von Alexandria und dem zu beginnen Elemente.
Als Ägypten nach dem Tod von Alexander dem Großen in den Händen von Ptolemaios I. blieb, begann er sein Projekt in einer Schule in Alexandria.
Unter den Weisen, die an der Schule unterrichteten, war Euklid. Es wird spekuliert, dass seine Geburt um 325 v. Chr. Stammt. C. und sein Tod von 265 a. C. Wir können mit Sicherheit wissen, dass er in Platons Schule gegangen ist.
Mehr als dreißig Jahre lang unterrichtete Euklid in Alexandria und baute seine berühmten Elemente auf: Er begann, eine erschöpfende Beschreibung der Mathematik seiner Zeit zu schreiben. Euklids Lehren brachten hervorragende Schüler hervor, wie Archimedes und Apollonius von Perga.
Euklid wurde beauftragt, die unterschiedlichen Entdeckungen der alten Griechen in der EU zu strukturieren Elemente, aber im Gegensatz zu seinen Vorgängern beschränkt es sich nicht darauf, zu bestätigen, dass ein Satz wahr ist; Euklid bietet eine Demonstration.
Das Elemente Sie sind ein Kompendium von dreizehn Büchern. Nach der Bibel ist es das am meisten veröffentlichte Buch mit mehr als tausend Ausgaben.
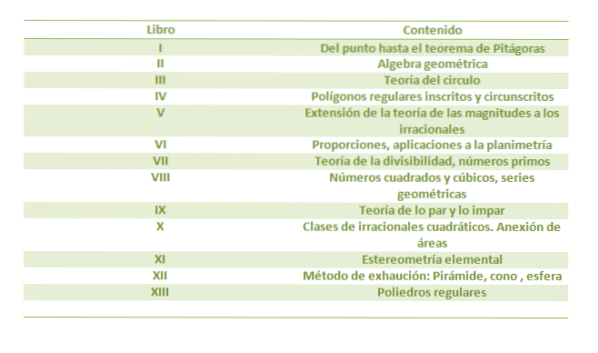
Das Elemente ist Euklids Meisterwerk auf dem Gebiet der Geometrie und bietet eine endgültige Behandlung der Geometrie von zwei Dimensionen (Ebene) und drei Dimensionen (Raum), wobei dies der Ursprung dessen ist, was wir heute als euklidische Geometrie kennen.
Die Elemente bestehen aus Definitionen, allgemeinen Begriffen und Postulaten (oder Axiomen), gefolgt von Theoremen, Konstruktionen und Beweisen..
- Ein Punkt ist das, was keine Teile hat.
- Eine Linie ist eine Länge ohne Breite.
- Eine gerade Linie ist eine Linie, die gleichermaßen in Bezug auf die Punkte liegt, die sich darin befinden.
- Wenn zwei Linien so geschnitten werden, dass die benachbarten Winkel gleich sind, werden die Winkel als rechte Winkel und die Linien als senkrecht bezeichnet.
- Parallele Linien sind solche, die sich in derselben Ebene niemals schneiden.
Nach diesen und anderen Definitionen präsentiert uns Euklid eine Liste mit fünf Postulaten und fünf Begriffen..
- Zwei Dinge, die einem Drittel entsprechen, sind einander gleich.
- Wenn dieselben Dinge zu denselben Dingen hinzugefügt werden, sind die Ergebnisse dieselben.
- Wenn gleiche Dinge von gleichen Dingen abgezogen werden, sind die Ergebnisse gleich.
- Dinge, die zueinander passen, sind einander gleich.
- Die Summe ist größer als ein Teil.
- Eine und nur eine Linie verläuft durch zwei verschiedene Punkte.
- Gerade Linien können unbegrenzt verlängert werden.
- Ein Kreis kann mit einem beliebigen Mittelpunkt und einem beliebigen Radius gezeichnet werden.
- Alle rechten Winkel sind gleich.
- Wenn eine gerade Linie zwei gerade Linien kreuzt, so dass sich die Innenwinkel derselben Seite zu weniger als zwei rechten Winkeln addieren, kreuzen sich die beiden Linien auf dieser Seite..
Dieses letzte Postulat ist als paralleles Postulat bekannt und wurde wie folgt umformuliert: "Für einen Punkt außerhalb einer Linie kann eine einzelne Parallele zur gegebenen Linie gezeichnet werden.".
Hier sind einige Sätze der Elemente Sie werden dazu dienen, Eigenschaften geometrischer Räume zu zeigen, in denen die fünf Postulate von Euklid erfüllt sind. Darüber hinaus veranschaulichen sie die logisch-deduktive Argumentation, die dieser Mathematiker verwendet hat.
Wenn zwei Dreiecke zwei Seiten haben und der Winkel zwischen ihnen gleich ist, sind die anderen Seiten und die anderen Winkel gleich..
ABC und A'B'C 'seien zwei Dreiecke mit AB = A'B', AC = A'C 'und gleichen Winkeln BAC und B'A'C'. Bewegen wir das Dreieck A'B'C 'so, dass A'B' mit AB und der Winkel B'A'C 'mit dem Winkel BAC übereinstimmt.
Die Linie A'C 'fällt also mit der Linie AC zusammen, so dass C' mit C zusammenfällt. Dann muss nach Postulat 1 die Linie BC mit der Linie B'C 'zusammenfallen. Daher fallen die beiden Dreiecke zusammen und folglich sind ihre Winkel und ihre Seiten gleich.
Wenn ein Dreieck zwei gleiche Seiten hat, sind die entgegengesetzten Winkel zu diesen Seiten gleich..
Angenommen, das Dreieck ABC hat die gleichen Seiten AB und AC.
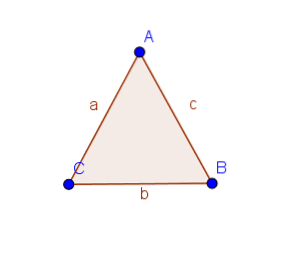
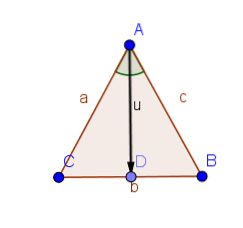
Die Dreiecke ABD und ACD haben also zwei gleiche Seiten und die Winkel zwischen ihnen sind gleich. Somit sind nach Satz 1.4 die Winkel ABD und ACD gleich.
Sie können eine Linie parallel zu einer Linie konstruieren, die durch einen bestimmten Punkt gegeben ist.
Bei einer gegebenen Linie L und einem Punkt P wird eine Linie M durch P gezogen und schneidet L. Dann wird eine Linie N durch P gezogen, die L schneidet. Nun wird eine Linie N durch P gezogen, die M schneidet und einen Winkel gleich bildet derjenige, den L mit M bildet.
N ist parallel zu L..
Angenommen, L und N sind nicht parallel und schneiden sich an einem Punkt A. Sei B ein Punkt in L jenseits von A. Betrachten Sie die Linie O, die durch B und P verläuft. Dann schneidet O M in Winkeln, die sich zu weniger als zwei addieren Gerade.
Dann muss die Linie O um 1,5 die Linie L auf der anderen Seite von M schneiden, so dass sich L und O an zwei Punkten schneiden, was dem Postulat 1 widerspricht. Daher müssen L und N parallel sein.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.