EIN surjektive Funktion ist eine Beziehung, in der jedes zur Codomäne gehörende Element ein Bild von mindestens einem Element der Domäne ist. Auch als Funktion bekannt auf, sind Teil der Klassifizierung von Funktionen in Bezug auf die Art und Weise, wie ihre Elemente zusammenhängen.
Zum Beispiel eine Funktion F: A. → B. definiert von F (x) = 2x
Welches liest "F. wie wäre es mit ZU bis um B. definiert von F (x) = 2x
Es ist Zeit, die Start- und Zielsätze zu definieren A und B.
A: 1, 2, 3, 4, 5 Nun die Werte oder Bilder, die jedes dieser Elemente bei der Auswertung in anzeigt F., wird die Elemente der Codomäne sein.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
So bildet sich das Ganze B: 2, 4, 6, 8, 10
Daraus kann geschlossen werden, dass:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 definiert von F (x) = 2x Es ist eine surjektive Funktion
Jedes Element der Codomäne muss aus mindestens einer Operation der unabhängigen Variablen durch die betreffende Funktion resultieren. Es gibt keine Einschränkung für Bilder. Ein Element der Codomäne kann ein Bild von mehr als einem Element der Domäne sein und es dennoch versuchen surjektive Funktion.
Das Bild zeigt 2 Beispiele mit surjektive Funktionen.
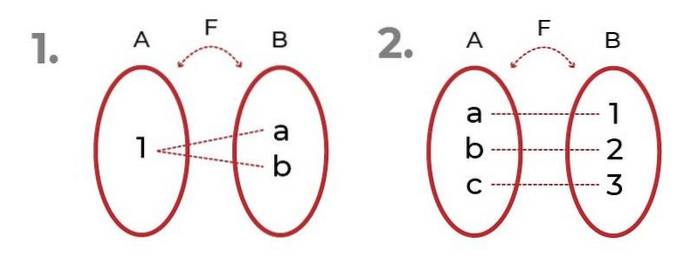
Im ersten Fall wird beobachtet, dass die Bilder auf dasselbe Element bezogen werden können, ohne das zu beeinträchtigen Surjektivität der Funktion.
Im zweiten sehen wir eine gerechte Verteilung zwischen Domain und Bildern. Dies führt zu bijektive Funktion, wo die Kriterien von Injektionsfunktion und Surjektivfunktion.
Eine andere Methode zur Identifizierung surjektive Funktionen, ist zu überprüfen, ob die Codomäne dem Funktionsbereich entspricht. Dies bedeutet, dass, wenn der Ankunftssatz den Bildern entspricht, die von der Funktion bei der Auswertung der unabhängigen Variablen bereitgestellt werden, Die Funktion ist surjektiv.
Artikelverzeichnis
Berücksichtigen surjektiv Für eine Funktion muss Folgendes erfüllt sein:
Sein F: D.F. → C.F.
∀ b ℮ C.F. UND zu ℮ D.F. / F (a) = b
Dies ist der algebraische Weg, um dies festzustellen für alle "b", die zu C gehörenF. Es gibt ein "a", das zu D gehörtF. so dass die in "a" ausgewertete Funktion F gleich "b" ist..
Surjektivität ist eine Besonderheit von Funktionen, bei denen die Codomäne und der Bereich ähnlich sind. Somit bilden die in der Funktion ausgewerteten Elemente den Ankunftssatz.
Manchmal eine Funktion, die nicht ist surjektiv, es kann bestimmten Bedingungen ausgesetzt werden. Diese neuen Bedingungen können es zu einem machen surjektive Funktion.
Alle Arten von Modifikationen an der Domäne und Codomäne der Funktion sind gültig, wobei das Ziel darin besteht, die Surjektivitätseigenschaften in der entsprechenden Beziehung zu erfüllen.
Um die Bedingungen von zu erfüllen Surjektivität Es müssen verschiedene Konditionierungstechniken angewendet werden, um sicherzustellen, dass sich jedes Element der Codomäne innerhalb des Satzes von Bildern der Funktion befindet.
A: [Alle reellen Zahlen]
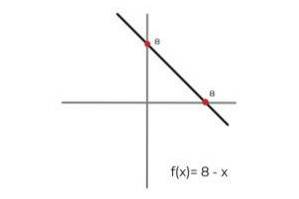
In diesem Fall beschreibt die Funktion eine durchgehende Linie, die alle reellen Zahlen sowohl in ihrer Domäne als auch in ihrem Bereich abdeckt. Weil der Funktionsumfang R.F. entspricht Codomäne R. Daraus kann man schließen:
F: R. → R. durch die Linie definiert F (x) = 8 - x ist ein surjektive Funktion.
Dies gilt für alle linearen Funktionen (Funktionen, deren größter Grad der Variablen eins ist).
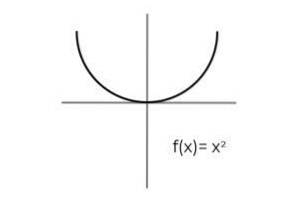
Das erste, was zu berücksichtigen ist, ist die Codomäne von F., welches aus den reellen Zahlen besteht R.. Es gibt keine Möglichkeit für die Funktion, negative Werte zurückzugeben, wodurch die realen Negative von den möglichen Bildern ausgeschlossen werden.
Konditionierung der Codomäne auf das Intervall [0 , ∞ ]. Es wird vermieden, Elemente der Codomäne durchgehend in Beziehung zu setzen F..
Die Bilder werden für Elementpaare der unabhängigen Variablen wiederholt, wie z x = 1 Y. x = - 1. Dies betrifft aber nur die Injektivität der Funktion, kein Problem für diese Studie.
Auf diese Weise kann geschlossen werden, dass:
F: R. →[0, ∞ ) definiert von F (x) = xzwei Es ist eine surjektive Funktion
F: R. → R. definiert von F (x) = Sen (x)
F: R. → R. definiert von F (x) = Cos (x)
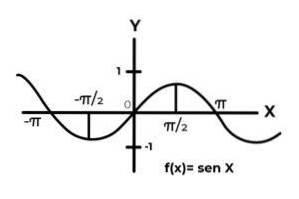
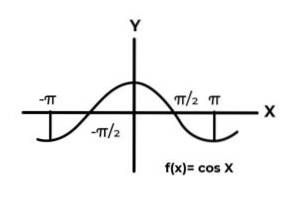
Das Verhalten der trigonometrischen Funktionen ähnelt dem von Wellen und ist sehr häufig, um Wiederholungen der abhängigen Variablen zwischen den Bildern zu finden. In den meisten Fällen ist der Funktionsbereich auch auf einen oder mehrere Sektoren der realen Linie beschränkt.
Dies ist der Fall bei den Sinus- und Cosinusfunktionen. Wo ihre Werte im Intervall [-1, 1] schwanken. Dieses Intervall muss die Codomäne konditionieren, um die Surjektivität der Funktion zu erreichen.
F: R. →[ -elf ] definiert von F (x) = Sen (x) Es ist eine surjektive Funktion
F: R. →[ -elf ]definiert von F (x) = Cos (x) Es ist eine surjektive Funktion
F: [0, ∞ ) → R. definiert von F (x) = ± √x bezeichnen, wenn es ein ist surjektive Funktion
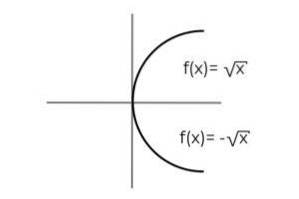
Die Funktion F (x) = ± √x Es hat die Besonderheit, dass es 2 abhängige Variablen für jeden Wert von "x" definiert. Das heißt, der Bereich erhält 2 Elemente für jedes Element, das in der Domäne erstellt wird. Für jeden Wert von "x" muss ein positiver und ein negativer Wert überprüft werden..
Bei der Beobachtung des Startsatzes wird angemerkt, dass die Domäne bereits eingeschränkt wurde, um die Unbestimmtheiten zu vermeiden, die bei der Bewertung einer negativen Zahl innerhalb einer geraden Wurzel entstehen.
Bei der Überprüfung des Funktionsbereichs wird darauf hingewiesen, dass jeder Wert der Codomäne zum Bereich gehört.
Auf diese Weise kann geschlossen werden, dass:
F: [0, ∞ ) → R. definiert von F (x) = ± √x Es ist eine surjektive Funktion
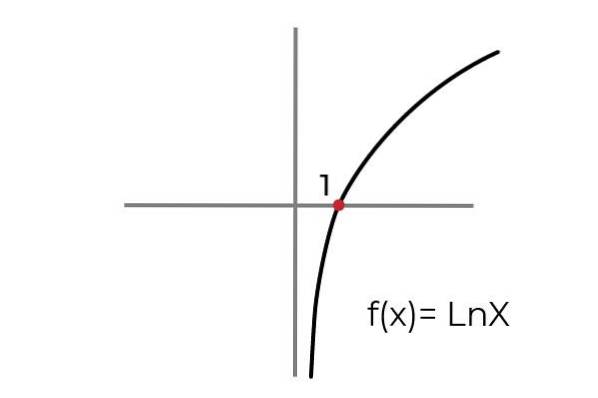
Wie in der Grafik gezeigt, die Funktion F (x) = Ln xEs ist für Werte von "x" größer als Null definiert. Während die Werte von "und" oder die Bilder einen beliebigen realen Wert annehmen können.
Auf diese Weise können wir die Domain von einschränken F (x) = zu Intervall (0 , ∞ )
Solange der Funktionsbereich als Satz reeller Zahlen beibehalten werden kann R..
In Anbetracht dessen kann geschlossen werden, dass:
F: [0, ∞ ) → R. definiert von F (x) = Ln x Es ist eine surjektive Funktion
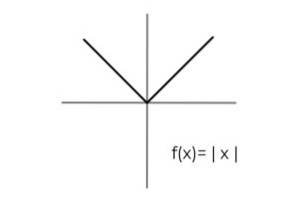
Die Domäne der Funktion gilt für alle reellen Zahlen R.. Auf diese Weise muss die einzige Konditionierung in der Codomäne durchgeführt werden, wobei zu berücksichtigen ist, dass die Absolutwertfunktion nur positive Werte berücksichtigt..
Wir fahren fort, die Codomäne der Funktion zu bestimmen, die sie dem Rang derselben gleichsetzt
[0 , ∞ )
Nun kann gefolgert werden, dass:
F: [0, ∞ ) → R. definiert von F (x) = | x | Es ist eine surjektive Funktion
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.