
Absolute Frequenzformel, Berechnung, Verteilung, Beispiel
Das Absolute Häufigkeit Es ist definiert als die Häufigkeit, mit der dieselben Daten innerhalb des Satzes von Beobachtungen einer numerischen Variablen wiederholt werden. Die Summe aller absoluten Frequenzen entspricht der Summe der Daten.
Wenn Sie viele Werte einer statistischen Variablen haben, ist es zweckmäßig, sie entsprechend zu organisieren, um Informationen über ihr Verhalten zu extrahieren. Solche Informationen werden durch die Maße der zentralen Tendenz und die Maße der Streuung gegeben..
Bei der Berechnung dieser Maßnahmen werden die Daten durch die Häufigkeit dargestellt, mit der sie in allen Beobachtungen auftreten..
Das folgende Beispiel zeigt, wie aufschlussreich die absolute Häufigkeit der einzelnen Daten ist. In der ersten Maihälfte waren dies die meistverkauften Cocktailkleidgrößen eines bekannten Damenbekleidungsgeschäfts:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Wie viele Kleider werden in einer bestimmten Größe verkauft, zum Beispiel in Größe 10? Die Eigentümer sind daran interessiert zu wissen, wie man bestellt.
Die Reihenfolge der Daten erleichtert das Zählen. Insgesamt gibt es genau 30 Beobachtungen, die von der kleinsten bis zur größten Größe wie folgt geordnet sind:
4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10;; 10;; 10;; 10;; 10;; 10;; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18
Und jetzt ist es offensichtlich, dass Größe 10 6 Mal wiederholt wird, daher ist ihre absolute Frequenz gleich 6. Das gleiche Verfahren wird durchgeführt, um die absolute Häufigkeit der verbleibenden Größen herauszufinden..
Artikelverzeichnis
- 1 Formeln
- 1.1 Andere Frequenzen
- 2 So erhalten Sie die absolute Frequenz?
- 2.1 Tabellierung
- 2.2 Erweiterte Häufigkeitstabelle
- 3 Häufigkeitsverteilung
- 3.1 Häufigkeitsverteilung für gruppierte Daten
- 4 Beispiel
- 5 Übung gelöst
- 5.1 Lösung
- 6 Referenzen
Formeln
Die absolute Frequenz, bezeichnet als fich, ist gleich der Häufigkeit, mit der ein bestimmter Wert X erreicht wirdich ist innerhalb der Gruppe von Beobachtungen.
Unter der Annahme, dass die Gesamtzahl der Beobachtungen N Werte ist, muss die Summe aller absoluten Frequenzen gleich dieser Zahl sein:
∑fich = f1 + F.zwei + F.3 +... fn = N.
Andere Frequenzen
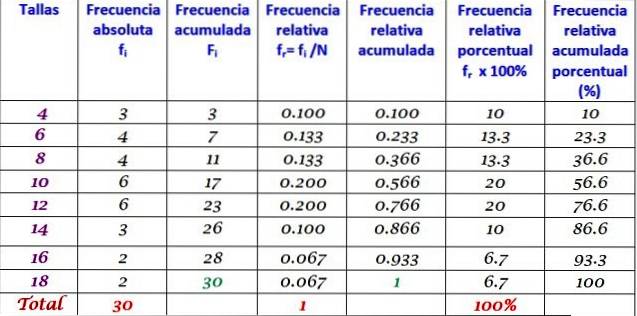
Wenn jeder Wert von fich geteilt durch die Gesamtzahl der Daten N haben wir die relative Frequenz F.r des X-Wertesich::
F.r = fich / N.
Relative Frequenzen sind Werte zwischen 0 und 1, da N immer größer als jedes f istich, aber die Summe muss gleich 1 sein.
Multiplizieren Sie jeden Wert von f mit 100r du hast die prozentuale relative Häufigkeit, deren Summe ist 100%:
Prozentuale relative Häufigkeit = (fich / N) x 100%
Wichtig ist auch kumulative Häufigkeit F.ich bis zu einer bestimmten Beobachtung ist dies die Summe aller absoluten Frequenzen bis einschließlich dieser Beobachtung:
F.ich = f1 + F.zwei + F.3 +... fich
Wenn die akkumulierte Frequenz durch die Gesamtzahl der Daten N geteilt wird, haben wir die kumulative relative Häufigkeit, was multipliziert mit 100 ergibt die prozentuale kumulative relative Häufigkeit.
So erhalten Sie die absolute Frequenz?
Um die absolute Häufigkeit eines bestimmten Werts zu ermitteln, der zu einem Datensatz gehört, werden alle vom niedrigsten zum höchsten Wert organisiert und die Häufigkeit, mit der der Wert angezeigt wird, wird gezählt.
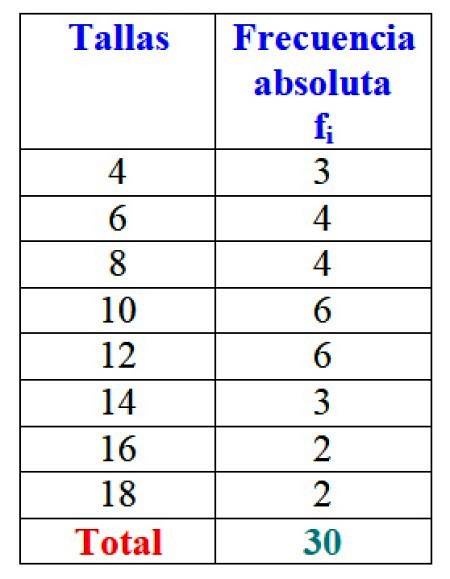
Im Beispiel der Kleidergrößen beträgt die absolute Häufigkeit von Größe 4 3 Kleider, dh f1 = 3. Für Größe 6 wurden 4 Kleider verkauft: fzwei = 4. In Größe 8 wurden auch 4 Kleider verkauft, f3 = 4 und so weiter.
Tabellierung
Die Gesamtergebnisse können in einer Tabelle dargestellt werden, in der die absoluten Häufigkeiten der einzelnen Ergebnisse aufgeführt sind:
Offensichtlich ist es vorteilhaft, die Informationen zu organisieren und auf einen Blick darauf zugreifen zu können, anstatt mit einzelnen Daten zu arbeiten.
Wichtig: Beachten Sie, dass beim Hinzufügen aller Werte der Spalte fich Sie erhalten immer die Gesamtzahl der Daten. Wenn nicht, müssen Sie die Buchhaltung überprüfen, da ein Fehler vorliegt.
Erweiterte Häufigkeitstabelle
Die obige Tabelle kann erweitert werden, indem die anderen Frequenztypen in aufeinanderfolgenden Spalten rechts hinzugefügt werden:
Häufigkeitsverteilung
Die Häufigkeitsverteilung ist das Ergebnis der Organisation der Daten in Bezug auf ihre Häufigkeit. Wenn Sie mit vielen Daten arbeiten, ist es zweckmäßig, sie in Kategorien, Intervalle oder Klassen zu gruppieren, jede mit ihren jeweiligen Häufigkeiten: absolut, relativ, akkumuliert und prozentual..
Ziel ist es, leichter auf die in den Daten enthaltenen Informationen zuzugreifen und diese richtig zu interpretieren, was nicht möglich ist, wenn sie in keiner Reihenfolge präsentiert werden..
Im Beispiel von Größen werden die Daten nicht gruppiert, da es sich nicht um zu viele Größen handelt, und können leicht manipuliert und berücksichtigt werden. Qualitative Variablen können auch auf diese Weise bearbeitet werden. Wenn die Daten jedoch sehr zahlreich sind, ist es besser, sie in Klassen zu gruppieren.
Häufigkeitsverteilung für gruppierte Daten
Beachten Sie Folgendes, um Ihre Daten in gleich große Klassen zu gruppieren:
-Klassengröße, -breite oder -breite: ist die Differenz zwischen dem höchsten Wert in der Klasse und dem niedrigsten.
Die Größe der Klasse wird bestimmt, indem der Rang R durch die Anzahl der zu berücksichtigenden Klassen geteilt wird. Der Bereich ist die Differenz zwischen dem Maximalwert der Daten und dem kleinsten wie folgt:
Klassengröße = Rang / Anzahl der Klassen.
-Klassenlimit: Intervall von der Untergrenze bis zur Obergrenze der Klasse.
-Klassennote: ist der Mittelpunkt des Intervalls, der als repräsentativ für die Klasse angesehen wird. Sie wird mit der Halbwertsumme der Obergrenze und der Untergrenze der Klasse berechnet.
-Anzahl der Klassen: Störformel kann verwendet werden:
Anzahl der Klassen = 1 + 3.322 log N.
Wobei N die Anzahl der Klassen ist. Da es sich normalerweise um eine Dezimalzahl handelt, wird sie auf die nächste Ganzzahl gerundet.
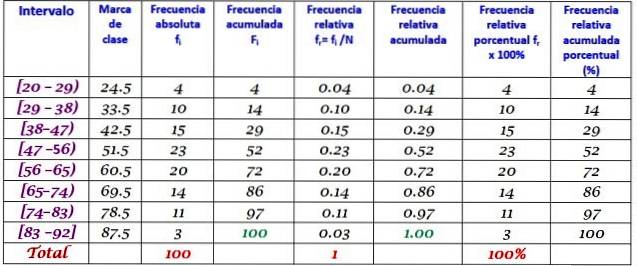
Beispiel
Eine Maschine in einer großen Fabrik ist aufgrund wiederkehrender Fehler außer Betrieb. Die aufeinanderfolgenden Inaktivitätsperioden in Minuten der Maschine werden nachstehend mit insgesamt 100 Daten aufgezeichnet:
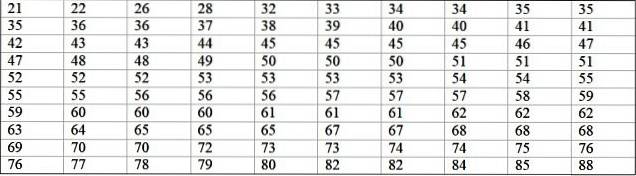
Zunächst wird die Anzahl der Klassen bestimmt:
Anzahl der Klassen = 1 + 3.322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8
Klassengröße = Bereich / Anzahl der Klassen = (88-21) / 8 = 8.375
Es ist auch eine Dezimalzahl, daher wird 9 als Klassengröße verwendet.
Die Klassennote ist der Durchschnitt zwischen der Ober- und Untergrenze der Klasse, zum Beispiel für die Klasse [20-29] gibt es eine Note von:
Klassennote = (29 + 20) / 2 = 24,5
Wir gehen auf die gleiche Weise vor, um die Klassenzeichen der verbleibenden Intervalle zu finden.
Übung gelöst
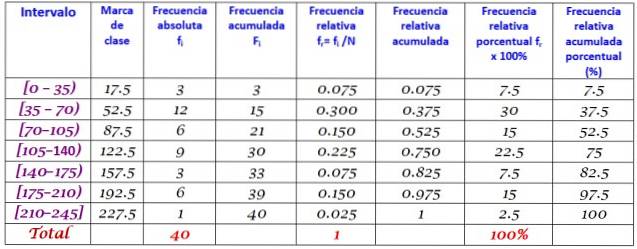
40 junge Leute gaben an, dass die Zeit in Minuten, die sie letzten Sonntag im Internet verbracht haben, die folgende war, die in aufsteigender Reihenfolge angeordnet wurde:
0; 12; zwanzig; 35; 35; 38; 40; Vier fünf; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Es wird gebeten, die Häufigkeitsverteilung dieser Daten zu konstruieren.
Lösung
Der Bereich R des Satzes von N = 40 Daten ist:
R = 220 - 0 = 220
Die Anwendung der Sturges-Formel zur Bestimmung der Anzahl der Klassen führt zu folgendem Ergebnis:
Anzahl der Klassen = 1 + 3.322 log N = 1 + 3,32 log 40 = 6,3
Da es sich um eine Dezimalzahl handelt, ist die unmittelbare Ganzzahl 7, daher werden die Daten in 7 Klassen gruppiert. Jede Klasse hat eine Breite von:
Klassengröße = Rang / Anzahl der Klassen = 220/7 = 31,4
Ein enger und runder Wert ist 35, daher wird eine Klassenbreite von 35 gewählt.
Klassenmarkierungen werden berechnet, indem die oberen und unteren Grenzen jedes Intervalls gemittelt werden, z. B. für das Intervall [0,35]:
Klassennote = (0 + 35) / 2 = 17,5
Gehen Sie mit den anderen Klassen genauso vor.
Schließlich werden die Frequenzen gemäß dem oben beschriebenen Verfahren berechnet, was zu der folgenden Verteilung führt:
Verweise
- Berenson, M. 1985. Statistik für Management und Wirtschaft. Interamericana S.A..
- Devore, J. 2012. Wahrscheinlichkeit und Statistik für Ingenieurwesen und Wissenschaft. 8 .. Auflage. Engagieren.
- Levin, R. 1988. Statistik für Administratoren. 2 .. Auflage. Prentice Halle.
- Spiegel, M. 2009. Statistik. Schaum-Serie. 4 .. Auflage. Mcgraw Hügel.
- Walpole, R. 2007. Wahrscheinlichkeit und Statistik für Ingenieurwissenschaften und Naturwissenschaften. Pearson.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.