Elektrischer Feldfluss

Was ist elektrischer Feldfluss??

Das elektrischer Feldfluss oder einfach elektrischer Fluss ist eine skalare Größe, die proportional zur Anzahl der elektrischen Feldlinien ist, die durch eine Oberfläche verlaufen. Es wird mit dem griechischen Großbuchstaben Φ (phi) bezeichnet..

Das elektrische Feld "fließt" nicht so wie ein Wasserstrom, obwohl die Stromlinien des Fluids denen des elektrischen Feldes ähneln..

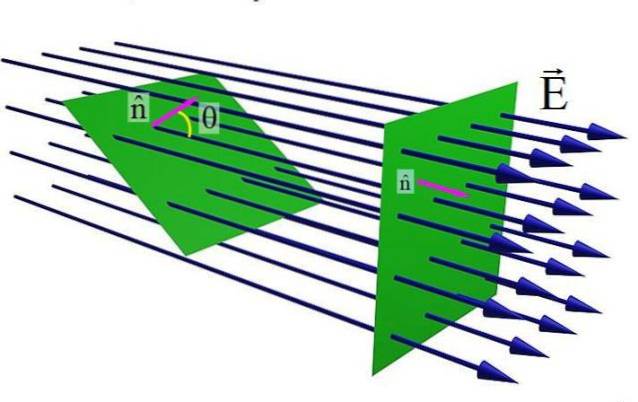
Die obige Abbildung zeigt eine flache Oberfläche, die von einem elektrischen Feld durchzogen wird UND. Wenn der Einheitsvektor senkrecht zur Oberfläche ist n und das Feld UND parallel sind, ist die Anzahl der Feldlinien, die die Oberfläche kreuzen, maximal. Aber als Winkel θ zwischen n Y. UND, Die Anzahl der Linien, die durch die grüne Fläche verlaufen, ist geringer.

Andererseits hängt der elektrische Feldfluss auch von der Größe von ab UND, denn je größer dies ist, desto mehr Feldlinien kreuzen die Oberfläche. Und je größer die Fläche S der Oberfläche ist, desto größer ist natürlich die Strömung, so dass die folgende Gleichung aufgestellt wird:

Φ = E ∙ Scosθ

Dieser Ausdruck stimmt mit dem Punktprodukt zwischen den Vektoren überein UND Y. n::

Φ = (UND • • n) S.

Die Einheit für den elektrischen Feldfluss im SI International System of Units ist Nm^zwei/ C (Newton x Quadratmeter / Coulomb). Alternativ bleibt der elektrische Fluss in (V ∙ m), da das Feld auch in V / m (Volt über Meter) gemessen wird..

Beispiele

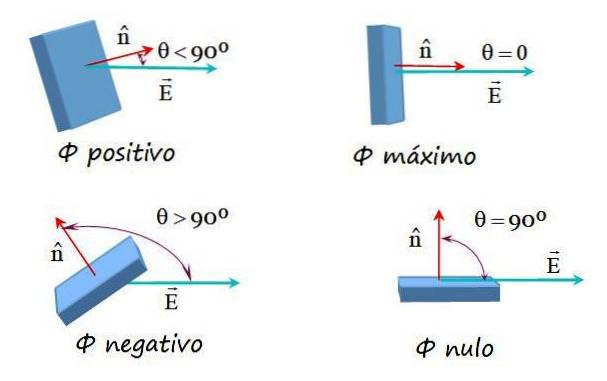
Gemäß der Definition kann der elektrische Fluss positiv, negativ oder gleich 0 sein. Der elektrische Feldfluss ist:

-Positiv, wenn Winkel θ zwischen UND Y. n ist kleiner als 90º, da cos & thgr; größer als Null ist.

-Negativ, wenn der Winkel größer als 90º ist, weil dann cos & thgr; kleiner als Null ist.

-Null, wenn θ genau 90º ist, weil cos 90º = 0 ist und die Feldlinien in diesem Fall tangential zur Oberfläche sind.

-Auf der anderen Seite, wenn der Winkel zwischen UND Y. n gleich 0 ist, erhält der Durchfluss seinen Maximalwert.

Diese Möglichkeiten sind im folgenden Bild dargestellt:

Elektrischer Feldfluss auf einer beliebigen Oberfläche

Zuvor wurde der elektrische Feldfluss im besonderen Fall eines auf eine ebene Fläche einfallenden gleichmäßigen Feldes bestimmt. Für eine Oberfläche beliebiger Form S und / oder eines ungleichmäßigen elektrischen Feldes ist der Winkel zwischen UND Y. n kann von Punkt zu Punkt variieren.

In der folgenden Abbildung gibt es zwei Beispiele: links eine gekrümmte Fläche und rechts eine geschlossene Fläche.

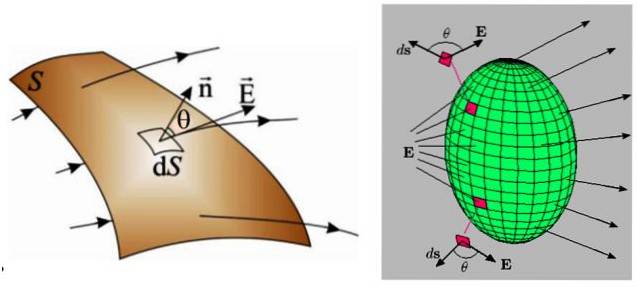
In beiden Fällen ist die Oberfläche in viel kleinere Bereiche von infinitesimaler Größe unterteilt, die als dS bezeichnet werden und durch die ein Fluss auch infinitesimal dΦ fließt:

dΦ = (UND• •n) dS = (Ecosθ) dS

Das Gesamtfeld wird erhalten, indem alle diese infinitesimalen Beiträge addiert werden:

Bei geschlossenen Flächen, n zeigt immer nach außen, daher hat die Strömung ein + Vorzeichen, wenn sie für S ausgeprägt ist, da der Winkel zwischen UND Y. n ist kleiner als 90º und Vorzeichen - wenn das Feld eingeht, weil dann der Winkel zwischen UND Y. n ist größer als 90º (siehe Abbildung 2).

Beachten Sie, dass in der geschlossenen Fläche rechts die Anzahl der in die Oberfläche eintretenden Feldlinien gleich der Anzahl der austretenden Linien ist. Daher ist der Nettofluss, definiert als die algebraische Summe des eingehenden und des ausgehenden Flusses, Null.

Die Quelle des elektrischen Feldes befindet sich in diesem Fall außerhalb der Oberfläche, der Nettofluss würde sich jedoch von 0 unterscheiden, wenn sich die Quelle des elektrischen Feldes (die Ladungsverteilung) innerhalb der Oberfläche befindet..

Ausbildung

Übung 1

Es hat ein elektrisches Feld UND = 3,5 kN / C. x und eine flache rechteckige Oberfläche mit einer Breite von 0,35 m und einer Länge von 0,7 m. Finden Sie den elektrischen Feldfluss durch das Rechteck in den folgenden Fällen:

a) Die Oberfläche verläuft parallel zur yz-Ebene.

b) Das Rechteck ist parallel zur xy-Ebene.

c) Die Normale der Ebene bildet mit der x-Achse einen Winkel von 40º und enthält die y-Achse.

Lösung für

Der Normalenvektor und der elektrische Feldvektor sind parallel, daher beträgt der Winkel θ zwischen ihnen 0º und der elektrische Fluss:

Φ = (E ∙ S) cos 0 = E ∙ S.

Die Fläche S des Rechtecks ​​ist:

S = 0,35 m × 0,7 m = 0,245 m^zwei

Einsetzen in Φ:

Φ = E ∙ S = 3,5 x 10³ N / C × 0,245 m^zwei = 857,5 Nm^zwei / C..

Lösung b

Der elektrische Feldfluss ist 0, da die Vektoren UND Y. n sind senkrecht zueinander.

Lösung c

Der Winkel θ zwischen dem Feld UND und der normale Vektor n beträgt 40º (siehe Abbildung), daher:

Φ = E ∙ S ∙ cos θ = 3,5 x 10³ N / C × 0,245 m^zwei × cos 40º = 656,9 Nm^zwei / C..

Übung 2

Berechnen Sie den elektrischen Feldfluss, der eine positive Punktladung q erzeugt_oder = 2μC in der Mitte einer Kugel mit dem Radius R = 5 cm.

Lösung

Das durch die Ladung q erzeugte Feld_oder Es ist nicht einheitlich, aber aus dem Coulombschen Gesetz ist bekannt, dass es auf der Oberfläche der Kugel eine Größe von:

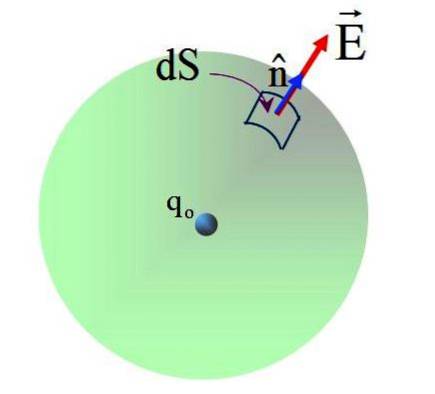
Das Feld hat eine radiale Richtung und den Normalenvektor n, Daher ist der Winkel zwischen beiden Vektoren an jedem Punkt der sphärischen Oberfläche 0. Einsetzen in:

Es muss:

Das Integral von dS über die gesamte sphärische Oberfläche S ist seine Fläche, die 4πR beträgt^zwei, So:

Sein Wert ist:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m^zwei/ C = 2,3 × 10⁵ N⋅m^zwei/ C.

Verweise

1. Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
2. Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 5. Elektrostatik. Herausgegeben von Douglas Figueroa (USB).
3. Giambattista, A. 2010. Physik. 2 .. Ed. McGraw Hill.
4. Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
5. Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1. Pearson.