Gemeinsamer Faktor durch Gruppierung von Begriffen, Beispiele, Übungen

Das gemeinsamer Faktor durch Gruppierung von Begriffen ist eine algebraische Prozedur, mit der Sie einige algebraische Ausdrücke in Form von Faktoren schreiben können. Um dieses Ziel zu erreichen, ist es zunächst erforderlich, den Ausdruck angemessen zu gruppieren und zu beobachten, dass jede so gebildete Gruppe tatsächlich einen gemeinsamen Faktor hat.

Die richtige Anwendung der Technik erfordert etwas Übung, aber in kurzer Zeit können Sie sie beherrschen. Schauen wir uns zunächst ein anschauliches Beispiel an, das Schritt für Schritt beschrieben wird. Dann kann der Leser das Gelernte in jeder der Übungen anwenden, die später erscheinen werden.

Angenommen, Sie müssen den folgenden Ausdruck berücksichtigen:

2x^zwei + 2xy - 3zx - 3zy

Dieser algebraische Ausdruck besteht aus 4 Monomen oder Begriffen, die durch + und - Zeichen getrennt sind, nämlich:

2x^zwei, 2xy, -3zx, -3zy

Bei genauerer Betrachtung ist x den ersten drei gemeinsam, aber nicht dem letzten, während y dem zweiten und vierten gemeinsam ist und z dem dritten und vierten gemeinsam ist..

Im Prinzip gibt es also keinen gemeinsamen Faktor für die vier Begriffe gleichzeitig, aber wenn sie wie im nächsten Abschnitt gezeigt gruppiert werden, ist es möglich, dass einer erscheint, der hilft, den Ausdruck als Produkt von zwei oder zu schreiben mehr Faktoren.

Artikelverzeichnis

• 1 Beispiele
• 2 Wichtige Fragen zum gemeinsamen Faktor durch Gruppierung
• 3 Übungen
  • 3.1 - Übung 1
  • 3.2 - Übung 2
• 4 Referenzen

Beispiele

Faktor der Ausdruck: 2x^zwei + 2xy - 3zx - 3zy

Schritt 1:: Gruppe

2x^zwei + 2xy - 3zx - 3zy = (2x^zwei + 2xy) + (-3zx - 3zy)

Schritt 2: Finden Sie den gemeinsamen Faktor jeder Gruppe

2x^zwei + 2xy - 3zx - 3zy =

= (2x^zwei + 2xy) - (3zx + 3zy) =

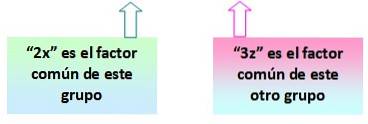
= 2x (x + y) - 3z (x + y)

ichwichtig:: das negative Vorzeichen Dies ist auch ein gemeinsamer Faktor, der berücksichtigt werden muss.

Beachten Sie nun, dass die Klammern (x + y) in den beiden durch Gruppierung erhaltenen Begriffen wiederholt werden. Das ist der gemeinsame Faktor, der gesucht wurde.

Schritt 3: Faktorisieren Sie den gesamten Ausdruck

2x^zwei + 2xy - 3zx - 3zy = (x + y) (2x - 3z)

Mit dem vorherigen Ergebnis wurde das Ziel des Factorings erreicht, das nichts anderes ist, als einen algebraischen Ausdruck, der auf Additionen und Subtraktionen von Begriffen basiert, in das Produkt von zwei oder mehr Faktoren umzuwandeln, in unserem Beispiel von: (x + y) y (2x - 3z).

Wichtige Fragen zum gemeinsamen Faktor durch Gruppierung

Fehler 1: Woher wissen, dass das Ergebnis korrekt ist??

Antworten: Die Verteilungseigenschaft wird auf das erhaltene Ergebnis angewendet. Nach dem Reduzieren und Vereinfachen muss der so erzielte Ausdruck mit dem Original übereinstimmen. Wenn nicht, liegt ein Fehler vor.

Im vorherigen Beispiel arbeiten wir umgekehrt mit dem Ergebnis, um zu überprüfen, ob es korrekt ist:

(x + y) (2x - 3z) = 2x^zwei -3zx + 2xy - 3zy

Da die Reihenfolge der Addenden die Summe nicht ändert, werden nach Anwendung der Verteilungseigenschaft alle ursprünglichen Begriffe zurückgegeben, einschließlich Zeichen, daher ist die Faktorisierung korrekt.

Frage 2: Könnte es anders gruppiert worden sein?

Antworten: Es gibt algebraische Ausdrücke, die mehr als eine Form der Gruppierung zulassen, und andere, die dies nicht tun. Im ausgewählten Beispiel kann der Leser andere Möglichkeiten selbst ausprobieren, z. B. die Gruppierung wie folgt:

2x^zwei + 2xy - 3zx - 3zy = (2x^zwei- 3zx) + (2xy - 3zy)

Und Sie können überprüfen, ob das Ergebnis das gleiche ist, wie es hier erhalten wurde. Das Finden der optimalen Gruppierung ist eine Frage der Praxis.

Frage 3: Warum ist es notwendig, einem algebraischen Ausdruck einen gemeinsamen Faktor zu entnehmen??

Antworten: Weil es Anwendungen gibt, in denen der faktorisierte Ausdruck Berechnungen erleichtert. Angenommen, Sie möchten 2x ausführen^zwei + 2xy - 3zx - 3zy gleich 0. Was wären die Möglichkeiten?

Um diese Frage zu beantworten, ist die faktorisierte Version in Bezug auf die ursprüngliche Entwicklung viel nützlicher. Es wird so angegeben:

(x + y) (2x - 3z) = 0

Eine Möglichkeit, dass der Ausdruck 0 ist, ist x = -y, unabhängig vom Wert von z. Und das andere ist, dass x = (3/2) z ist, unabhängig vom Wert von y.

Ausbildung

- Übung 1

Nehmen Sie einen gemeinsamen Faktor des folgenden Ausdrucks, indem Sie Begriffe gruppieren:

axe + ay + bx + von

Lösung

Die ersten beiden werden mit dem gemeinsamen Faktor "a" und die letzten beiden mit dem gemeinsamen Faktor "b" gruppiert:

ax + ay + bx + by = a (x + y) + b (x + y)

Sobald dies erledigt ist, wird ein neuer gemeinsamer Faktor aufgedeckt, nämlich (x + y), so dass:

ax + ay + bx + by = a (x + y) + b (x + y) = (x + y) (a + b)

Ein anderer Weg, um zu gruppieren

Dieser Ausdruck unterstützt eine andere Art der Gruppierung. Mal sehen, was passiert, wenn die Begriffe neu angeordnet werden und eine Gruppe mit denen gebildet wird, die x enthalten, und eine andere mit denen, die y enthalten:

ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b)

Auf diese Weise ist der neue gemeinsame Faktor (a + b):

ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b) = (x + y) (a + b)

Dies führt zu demselben Ergebnis wie bei der ersten getesteten Gruppierung.

- Übung 2

Der folgende algebraische Ausdruck muss als Produkt zweier Faktoren geschrieben werden:

3 ..³ - 3 ..^zweib + 9ab^zwei-zu^zwei+ab-3b^zwei

Lösung

Dieser Ausdruck enthält 6 Begriffe. Versuchen wir, zuerst und viertens, zweitens und drittens und schließlich fünftes und sechstes zu gruppieren:

3 ..³ - 3 ..^zweib + 9ab^zwei-zu^zwei+ab-3b^zwei = (3a³ -zu^zwei) + (- 3a^zweib + 9ab^zwei) + (ab-3b^zwei)

Jetzt wird jede Klammer berücksichtigt:

= (3a³ -zu^zwei) + (- 3a^zweib + 9ab^zwei) + (ab -3b^zwei) = a^zwei (3a - 1) + 3ab (3b - a) + b (a - 3b)

Auf den ersten Blick scheint die Situation kompliziert gewesen zu sein, aber der Leser sollte nicht entmutigt werden, da wir den letzten Begriff neu schreiben werden:

zu^zwei (3a - 1) + 3ab (3b - a) + b (a - 3b) = a^zwei (3a - 1) + 3ab (3b-a) - b (3b-a)

Die letzten beiden Terme haben jetzt einen gemeinsamen Faktor, nämlich (3b-a), sodass sie berücksichtigt werden können. Es ist sehr wichtig, die erste Amtszeit nicht aus den Augen zu verlieren^zwei (3a - 1), die weiterhin alles als Hinzufügen begleiten muss, auch wenn Sie nicht damit arbeiten:

zu^zwei (3a - 1) + 3ab (3b-a) - b (3b-a) = a^zwei (3a - 1) + (3b-a) (3ab-b)

Der Ausdruck wurde auf zwei Begriffe reduziert und im letzten wird ein neuer gemeinsamer Faktor entdeckt, nämlich "b". Jetzt bleibt es:

zu^zwei (3a - 1) + (3b-a) (3ab-b) = a^zwei (3a - 1) + b (3b - a) (3a - 1)

Der nächste häufig auftretende Faktor ist 3a - 1:

zu^zwei (3a - 1) + b (3b - a) (3a - 1) = (3a - 1) [a^zwei + b (3b-a)]

Oder wenn Sie ohne Klammern bevorzugen:

(3a - 1) [a^zwei + b (3b-a)] = (3a - 1) (a^zwei -ab + 3b^zwei)

Kann der Leser einen anderen Weg der Gruppierung finden, der zum gleichen Ergebnis führt??

Verweise

1. Baldor, A. 1974. Elementare Algebra. Kultur Venezolana S.A..
2. Jiménez, R. 2008. Algebra. Prentice Halle.
3. Hauptfälle des Factorings. Wiederhergestellt von: julioprofe.net.
4. UNAM. Grundlegende Mathematik: Faktorisierung durch Gruppierung von Begriffen. Fakultät für Rechnungswesen und Verwaltung.
5. Zill, D. 1984. Algebra und Trigonometrie. MacGraw Hill.