
Translationale Gleichgewichtsbestimmung, Anwendungen, Beispiele
Das Translationsgleichgewicht Es ist ein Zustand, in dem ein Objekt als Ganzes gefunden wird, wenn alle auf es einwirkenden Kräfte kompensiert werden, was zu einer Nettokraft von Null führt. Mathematisch äquivalent zu der Aussage, dass F.1+ F.zwei + F.3 +…. = 0, wobei F.1, F.zwei, F.3... die beteiligten Kräfte.
Die Tatsache, dass sich ein Körper im Translationsgleichgewicht befindet, bedeutet nicht, dass er notwendigerweise in Ruhe ist. Dies ist ein besonderer Fall der oben angegebenen Definition. Das Objekt kann in Bewegung sein, aber ohne Beschleunigung ist dies eine gleichmäßige geradlinige Bewegung.

Wenn der Körper also in Ruhe ist, geht es so weiter. Und wenn es bereits Bewegung hat, hat es eine konstante Geschwindigkeit. Im Allgemeinen ist die Bewegung eines Objekts eine Komposition aus Übersetzungen und Rotationen. Die Übersetzungen können wie in Abbildung 2 dargestellt sein: linear oder krummlinig.
Wenn jedoch einer der Punkte des Objekts festgelegt ist, besteht die einzige Chance, dass es sich bewegen kann, darin, sich zu drehen. Ein Beispiel hierfür ist eine CD, deren Mitte fest ist. Die CD kann sich um eine Achse drehen, die durch diesen Punkt verläuft, aber nicht verschieben.
Wenn Objekte feste Punkte haben oder auf Oberflächen abgestützt sind, sprechen wir von Links. Die Verknüpfungen interagieren und begrenzen die Bewegungen, die das Objekt ausführen kann.
Artikelverzeichnis
- 1 Bestimmung des Translationsgleichgewichts
- 1.1 Ein Objekt drehen
- 1.2 Definition des Drehmoments
- 1.3 Gleichgewichtsbedingungen
- 2 Anwendungen
- 3 Beispiele für das Translationsgleichgewicht
- 3.1 Lösung
- 4 Referenzen
Bestimmung des Translationsgleichgewichts
Für ein Teilchen im Gleichgewicht gilt Folgendes:
F.R. = 0
Oder in Summationsnotation:
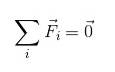
Es ist klar, dass die auf ihn einwirkenden Kräfte auf irgendeine Weise kompensiert werden müssen, damit sich ein Körper im Translationsgleichgewicht befindet, so dass ihre Resultierende Null ist..
Auf diese Weise erfährt das Objekt keine Beschleunigung und alle seine Partikel ruhen oder durchlaufen geradlinige Translationsbewegungen mit konstanter Geschwindigkeit..
Wenn sich Objekte jetzt drehen können, werden sie es im Allgemeinen tun. Deshalb bestehen die meisten Bewegungen aus Kombinationen von Translation und Rotation..
Ein Objekt drehen
Wenn das Rotationsgleichgewicht wichtig ist, muss möglicherweise sichergestellt werden, dass sich das Objekt nicht dreht. Dann muss untersucht werden, ob Drehmomente oder Momente darauf einwirken.
Das Drehmoment ist die Vektorgröße, von der die Rotationen abhängen. Es muss eine Kraft angewendet werden, aber der Angriffspunkt der Kraft ist auch wichtig. Betrachten Sie zur Verdeutlichung der Idee ein erweitertes Objekt, auf das eine Kraft einwirkt F. und mal sehen, ob es in der Lage ist, eine Drehung um eine Achse O zu erzeugen.
Es ist bereits gedacht, dass beim Schieben des Objekts am Punkt P mit der Kraft F., Es ist möglich, ihn gegen den Uhrzeigersinn um den Punkt O zu drehen. Wichtig ist aber auch die Richtung, in die die Kraft ausgeübt wird. Zum Beispiel wird das Objekt durch die auf die Figur in der Mitte ausgeübte Kraft nicht gedreht, obwohl es es sicherlich bewegen kann..
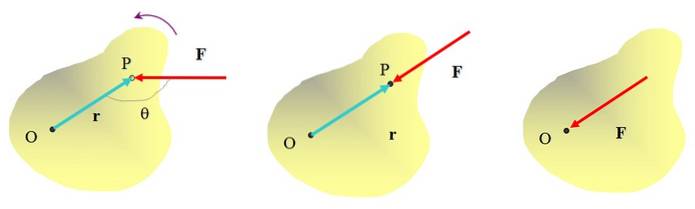
Durch direktes Aufbringen von Kraft auf Punkt O wird das Objekt ebenfalls nicht gedreht. Es ist also klar, dass zur Erzielung eines Rotationseffekts die Kraft in einem bestimmten Abstand von der Rotationsachse aufgebracht werden muss und ihre Wirkungslinie nicht durch diese Achse verlaufen darf..
Definition des Drehmoments
Das Drehmoment oder Moment einer Kraft, bezeichnet als τ, die Vektorgröße, die für die Zusammenstellung all dieser Tatsachen verantwortlich ist, ist definiert als:
τ = r x F.
Der Vektor r es ist von der Drehachse zum Angriffspunkt der Kraft gerichtet und die Beteiligung des Winkels zwischen r und F ist wichtig. Daher wird die Größe des Drehmoments ausgedrückt als:
τ = r.F.sen. Was
Das effektivste Drehmoment tritt auf, wenn r Y. F. sie sind senkrecht.
Wenn nun gewünscht wird, dass es keine Rotationen gibt oder diese mit konstanter Winkelbeschleunigung stattfinden, ist es notwendig, dass die Summe der auf das Objekt einwirkenden Drehmomente Null ist, analog zu dem, was für die Kräfte berücksichtigt wurde:
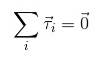
Gleichgewichtsbedingungen
Gleichgewicht bedeutet Stabilität, Harmonie und Gleichgewicht. Damit die Bewegung eines Objekts diese Eigenschaften aufweist, müssen die in den vorherigen Abschnitten beschriebenen Bedingungen angewendet werden:
1) F.1+ F.zwei + F.3 +…. = 0
2) τ1+ τzwei + τ3 +…. = 0
Die erste Bedingung garantiert das Translationsgleichgewicht und die zweite das Rotationsgleichgewicht. Beide müssen erfüllt sein, wenn das Objekt in bleiben soll statisches Gleichgewicht (keine Bewegung jeglicher Art).
Anwendungen
Gleichgewichtsbedingungen gelten für viele Strukturen, da beim Bau von Gebäuden oder verschiedenen Objekten die Absicht besteht, dass ihre Teile in denselben relativen Positionen zueinander bleiben. Mit anderen Worten, dass sich das Objekt nicht zerlegt.
Dies ist zum Beispiel wichtig, wenn Sie Brücken bauen, die unter den Füßen fest bleiben, oder wenn Sie bewohnbare Strukturen entwerfen, die ihre Position nicht ändern oder zum Umkippen neigen..
Obwohl angenommen wird, dass eine gleichmäßige geradlinige Bewegung eine extreme Vereinfachung der Bewegung darstellt, die in der Natur selten auftritt, muss beachtet werden, dass die Lichtgeschwindigkeit im Vakuum konstant ist und die des Schalls in der Luft auch, wenn man das Medium als homogen betrachtet.
In vielen künstlichen mobilen Strukturen ist es wichtig, dass eine konstante Geschwindigkeit eingehalten wird: zum Beispiel auf Rolltreppen und Montagelinien.
Beispiele für das Translationsgleichgewicht
Dies ist die klassische Übung der Spannungen, die die Lampe im Gleichgewicht halten. Es ist bekannt, dass die Lampe 15 kg wiegt. Finden Sie die Größen der Spannungen, die erforderlich sind, um es in dieser Position zu halten.
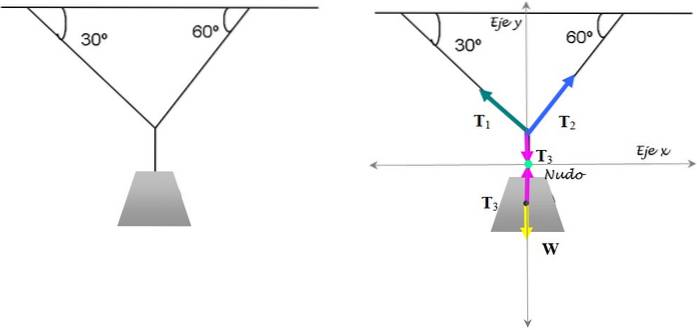
Lösung
Um es zu lösen, konzentrieren wir uns auf den Knoten, an dem sich die drei Saiten treffen. Die jeweiligen Freikörperdiagramme für den Knoten und für die Lampe sind in der obigen Abbildung dargestellt..
Das Gewicht der Lampe beträgt W = 5 kg. 9,8 m / szwei = 49 N.. Damit sich die Lampe im Gleichgewicht befindet, ist es ausreichend, dass die erste Gleichgewichtsbedingung erfüllt ist:
T.3 - W = 0
T.3 = W = 49 N..
Spannungen T.1 Y. T.zwei muss sich zersetzen:
T.1y + T.2 und - T.3 = 0 (Summe der Kräfte entlang der y-Achse)
-T.1x +T.2x = 0 (Summe der Kräfte entlang der x-Achse)
Anwendung der Trigonometrie:
T.1.cos 60º + T.zwei .cos 30º = 49
- T.1.sen60º + T.zwei.sin30º = 0
Es ist ein System aus zwei Gleichungen mit zwei Unbekannten, deren Antwort lautet: T.1 = 24,5 N. Y. T.zwei = 42,4 N..
Verweise
- Rex, A. 2011. Grundlagen der Physik. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7ma. Ed. Lernen einbinden. 120 - 124.
- Serway, R., Vulle, C. 2011. Grundlagen der Physik. 9n / A Ed. Lernen einbinden. 99-112.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Physik. Addison Wesley. 332-346.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.