
Polynomgleichungen (mit gelösten Übungen)

Das Polynomgleichungen Sie sind eine Aussage, die die Gleichheit von zwei Ausdrücken oder Mitgliedern erhöht, wobei mindestens einer der Begriffe, aus denen jede Seite der Gleichheit besteht, Polynome P (x) sind. Diese Gleichungen werden nach dem Grad ihrer Variablen benannt.
Im Allgemeinen ist eine Gleichung eine Aussage, die die Gleichheit zweier Ausdrücke festlegt, wobei in mindestens einer davon unbekannte Größen vorhanden sind, die als Variablen oder Unbekannte bezeichnet werden. Obwohl es viele Arten von Gleichungen gibt, werden sie im Allgemeinen in zwei Arten eingeteilt: algebraisch und transzendent..

Polynomgleichungen enthalten nur algebraische Ausdrücke, an denen eine oder mehrere Unbekannte beteiligt sein können. Je nach Exponent (Grad) können sie klassifiziert werden in: ersten Grad (linear), zweiten Grad (quadratisch), dritten Grad (kubisch), vierten Grad (quartisch), Grad größer oder gleich fünf und irrational.
Artikelverzeichnis
- 1 Funktionen
- 2 Arten
- 2.1 Erste Klasse
- 2.2 Zweite Klasse
- 2.3 Lösungsmittel
- 2.4 Hauptabschluss
- 3 Gelöste Übungen
- 3.1 Erste Übung
- 3.2 Zweite Übung
- 4 Referenzen
Eigenschaften
Polynomgleichungen sind Ausdrücke, die durch eine Gleichheit zwischen zwei Polynomen gebildet werden. das heißt, durch die endlichen Summen von Multiplikationen zwischen unbekannten Werten (Variablen) und festen Zahlen (Koeffizienten), wobei die Variablen Exponenten haben können und ihr Wert eine positive ganze Zahl sein kann, einschließlich Null.
Die Exponenten bestimmen den Grad oder die Art der Gleichung. Der Term des Ausdrucks mit dem Exponenten mit dem höchsten Wert repräsentiert den absoluten Grad des Polynoms.
Polynomgleichungen werden auch als algebraisch bezeichnet, ihre Koeffizienten können reelle oder komplexe Zahlen sein und die Variablen sind unbekannte Zahlen, die durch einen Buchstaben dargestellt werden, wie z. B.: "X".
Wenn die Variable "x" in P (x) durch einen Wert ersetzt wird, ist das Ergebnis gleich Null (0), dann erfüllt dieser Wert die Gleichung (es ist eine Lösung) und wird allgemein als Wurzel des Polynoms bezeichnet.
Wenn Sie eine Polynomgleichung entwickeln, möchten Sie alle Wurzeln oder Lösungen finden.
Typen
Es gibt verschiedene Arten von Polynomgleichungen, die nach der Anzahl der Variablen und auch nach dem Grad ihres Exponenten unterschieden werden.
Somit können die Polynomgleichungen - wobei sein erster Term ein Polynom ist, das ein einzelnes Unbekanntes hat, wenn man bedenkt, dass sein Grad eine beliebige natürliche Zahl (n) sein kann und der zweite Term Null ist - wie folgt ausgedrückt werden:
zun * xn + zun-1 * xn-1 +… + A.1 * x1 + zu0 * x0 = 0
Wo:
- zun, zun-1 bereits0, sind reelle Koeffizienten (Zahlen).
- zun ist anders als Null.
- Der Exponent n ist eine positive ganze Zahl, die den Grad der Gleichung darstellt.
- x ist die zu durchsuchende Variable oder Unbekannte.
Der absolute oder höhere Grad einer Polynomgleichung ist der Exponent mit dem höchsten Wert unter allen, die das Polynom bilden; Somit werden die Gleichungen klassifiziert als:
Erste Klasse
Polynomgleichungen ersten Grades, auch als lineare Gleichungen bekannt, sind solche, bei denen der Grad (der größte Exponent) gleich 1 ist, das Polynom die Form P (x) = 0 hat; und es besteht aus einem linearen und einem unabhängigen Term. Es ist wie folgt geschrieben:
ax + b = 0.
Wo:
- a und b sind reelle Zahlen und a ≠ 0.
- ax ist der lineare Term.
- b ist der unabhängige Begriff.
Zum Beispiel ist die Gleichung 13x - 18 = 4x.
Um lineare Gleichungen zu lösen, müssen alle Terme, die das unbekannte x enthalten, an eine Seite der Gleichheit übergeben werden, und diejenigen, die sie nicht haben, müssen auf die andere Seite verschoben werden, um sie zu lösen und eine Lösung zu erhalten:
13x - 18 = 4x
13x = 4x + 18
13x - 4x = 18
9x = 18
x = 18 ÷ 9
x = 2.
Somit hat die gegebene Gleichung nur eine Lösung oder Wurzel, nämlich x = 2.
Zweite Klasse
Polynomgleichungen zweiten Grades, auch als quadratische Gleichungen bekannt, sind solche, bei denen der Grad (der größte Exponent) gleich 2 ist, das Polynom die Form P (x) = 0 hat und aus einem quadratischen Term besteht, einem linearen und eine unabhängige. Es wird wie folgt ausgedrückt:
Axtzwei + bx + c = 0.
Wo:
- a, b und c sind reelle Zahlen und a ≠ 0.
- Axtzwei ist der quadratische Term und "a" ist der Koeffizient des quadratischen Terms.
- bx ist der lineare Term und "b" ist der Koeffizient des linearen Terms.
- c ist der unabhängige Begriff.
Lösungsmittel
Im Allgemeinen wird die Lösung für diese Art von Gleichungen gegeben, indem x aus der Gleichung gelöst wird, und es ist wie folgt, was als Auflösung bezeichnet wird:

Dort (bzwei - 4ac) heißt die Diskriminante der Gleichung und dieser Ausdruck bestimmt die Anzahl der Lösungen, die die Gleichung haben kann:
- Ja bzwei - 4ac) = 0, die Gleichung hat eine einfache Lösung, die doppelt ist; Das heißt, es wird zwei gleiche Lösungen geben.
- Ja bzwei - 4ac)> 0 hat die Gleichung zwei verschiedene reelle Lösungen.
- Ja bzwei - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).
Zum Beispiel haben wir die Gleichung 4xzwei + 10x - 6 = 0, um es zu lösen, identifizieren Sie zuerst die Begriffe a, b und c und setzen Sie es dann in die Formel ein:
a = 4
b = 10
c = -6.
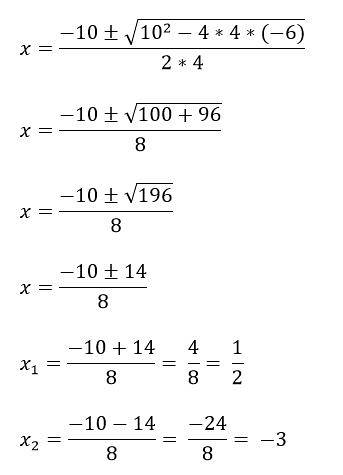
Es gibt Fälle, in denen die Polynomgleichungen zweiten Grades nicht alle drei Terme haben, und deshalb werden sie auf andere Weise gelöst:
- Für den Fall, dass die quadratischen Gleichungen nicht den linearen Term haben (dh b = 0), wird die Gleichung als ax ausgedrücktzwei + c = 0. Um es zu lösen, lösen Sie nach xzwei und die Quadratwurzeln werden auf jedes Mitglied angewendet, wobei zu beachten ist, dass die zwei möglichen Zeichen, die das Unbekannte haben kann, berücksichtigt werden müssen:
Axtzwei + c = 0.
xzwei = - c ÷ a
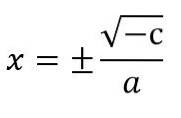
Zum Beispiel 5 xzwei - 20 = 0.
5 xzwei = 20
xzwei = 20 ÷ 5
x = ± √4
x = ± 2
x1 = 2.
xzwei = -2.
- Wenn die quadratische Gleichung keinen unabhängigen Term hat (dh c = 0), wird die Gleichung als ax ausgedrücktzwei + bx = 0. Um es zu lösen, müssen wir den gemeinsamen Faktor des unbekannten x im ersten Glied nehmen; Da die Gleichung gleich Null ist, ist es wahr, dass mindestens einer der Faktoren gleich 0 ist:
Axtzwei + bx = 0.
x (ax + b) = 0.
Sie müssen also:
x = 0.
x = -b ÷ a.
Zum Beispiel: Wir haben die Gleichung 5xzwei + 30x = 0. Erster Faktor:
5xzwei + 30x = 0
x (5x + 30) = 0.
Es werden zwei Faktoren erzeugt, nämlich x und (5x + 30). Es wird angenommen, dass eine davon gleich Null ist und die andere eine Lösung erhält:
x1 = 0.
5x + 30 = 0
5x = -30
x = -30 ≤ 5
xzwei = -6.
Höchste Note
Polynomgleichungen höheren Grades sind solche ab dem dritten Grad, die mit der allgemeinen Polynomgleichung für jeden Grad ausgedrückt oder gelöst werden können:
zun * xn + zun-1 * xn-1 +… + A.1 * x1 + zu0 * x0 = 0
Dies wird verwendet, weil eine Gleichung mit einem Grad größer als zwei das Ergebnis der Faktorisierung eines Polynoms ist; das heißt, es wird als Multiplikation von Polynomen vom Grad eins oder höher ausgedrückt, jedoch ohne echte Wurzeln.
Die Lösung dieser Art von Gleichungen ist direkt, da die Multiplikation zweier Faktoren gleich Null ist, wenn einer der Faktoren Null (0) ist; Daher muss jede der gefundenen Polynomgleichungen gelöst werden, indem jeder ihrer Faktoren gleich Null gesetzt wird.
Zum Beispiel haben wir die (kubische) Gleichung dritten Grades x3 + xzwei +4x + 4 = 0. Um es zu lösen, müssen die folgenden Schritte ausgeführt werden:
- Die Begriffe sind gruppiert:
x3 + xzwei +4x + 4 = 0
(x3 + xzwei ) + (4x + 4) = 0.
- Die Mitglieder werden zerlegt, um den gemeinsamen Faktor des Unbekannten zu erhalten:
xzwei (x + 1) + 4 (x + 1) = 0
(xzwei + 4)* *(x + 1) = 0.
- Auf diese Weise werden zwei Faktoren erhalten, die gleich Null sein müssen:
(xzwei + 4) = 0
(x + 1) = 0.
- Es ist ersichtlich, dass der Faktor (xzwei + 4) = 0 hat keine echte Lösung, während der Faktor (x + 1) = 0 ist. Die Lösung lautet also:
(x + 1) = 0
x = -1.
Gelöste Übungen
Lösen Sie die folgenden Gleichungen:
Erste Übung
(2xzwei + 5)* *(x - 3)* *(1 + x) = 0.
Lösung
In diesem Fall wird die Gleichung als Multiplikation von Polynomen ausgedrückt; das heißt, es wird berücksichtigt. Um es zu lösen, muss jeder Faktor gleich Null gesetzt werden:
- 2xzwei + 5 = 0, hat keine Lösung.
- x - 3 = 0
- x = 3.
- 1 + x = 0
- x = - 1.
Somit hat die gegebene Gleichung zwei Lösungen: x = 3 und x = -1.
Zweite Übung
x4 - 36 = 0.
Lösung
Es wurde ein Polynom angegeben, das als Differenz der Quadrate umgeschrieben werden kann, um zu einer schnelleren Lösung zu gelangen. Somit lautet die Gleichung:
(xzwei + 6)* *(xzwei - 6) = 0.
Um die Lösung der Gleichungen zu finden, werden beide Faktoren gleich Null gesetzt:
(xzwei + 6) = 0, hat keine Lösung.
(xzwei - 6) = 0
xzwei = 6
x = ± √6.
Somit hat die Anfangsgleichung zwei Lösungen:
x = √6.
x = - √6.
Verweise
- Andres, T. (2010). Mathematische Olympiade Tresure. Springer. New York.
- Angel, A. R. (2007). Elementare Algebra. Pearson Ausbildung,.
- Baer, R. (2012). Lineare Algebra und projektive Geometrie. Courier Corporation.
- Baldor, A. (1941). Algebra. Havanna: Kultur.
- Castaño, H. F. (2005). Mathematik vor der Analysis. Universität von Medellin.
- Cristóbal Sánchez, M. R. (2000). Mathematisches Handbuch zur olympischen Vorbereitung. Jaume I Universität.
- Kreemly Pérez, M. L. (1984). Höhere Algebra I..
- Massara, N. C.-L. (1995). Mathematik 3.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.