
Gleichungsformel ersten Grades, wie man sie löst, zum Beispiel Übungen
Das erster Grad oder lineare Gleichungen mit einem Unbekannten sind diejenigen, die als die Summe von zwei Begriffen wie folgt ausgedrückt werden können:
ax + b = 0
Wo A und B, mit zu ≠ 0 sind reelle Zahlen R oder auch komplexe C. Um dies zu lösen, werden Terme transponiert, was bedeutet, dass Terme von einer Seite der Gleichheit zur anderen geändert werden.
Um das Unbekannte zu lösen, wird der Term + b transponiert, der mit geändertem Vorzeichen auf die rechte Seite der Gleichheit gehen muss.
ax = -b
Dann wird der Wert von x wie folgt gelöscht:
x = - b / a
Als Beispiel werden wir die folgende Gleichung lösen:
6x - 5 = 4
Wir transponieren den Term -5 mit einem geänderten Vorzeichen auf die rechte Seite:
6x = 4 + 5
Dies entspricht dem Hinzufügen von 5 zu beiden Seiten der ursprünglichen Gleichung:
6x - 5 + 5 = 4 + 5 → 6x = 9
Und jetzt lösen wir das unbekannte "x":
x = 9/6 = 3/2
Dies entspricht der Division beider Seiten der Gleichheit durch 6. Wir können also Folgendes verwenden, um die Lösung zu erhalten:
-Die gleiche Menge kann von beiden Seiten der Gleichheit in einer Gleichung addiert oder subtrahiert werden, ohne sie zu ändern.
-Sie können auch alle Terme links und rechts von der Gleichung mit demselben Betrag multiplizieren (oder dividieren).
-Und wenn beide Glieder einer Gleichung zur gleichen Potenz erhoben werden, ändert sich auch die Gleichheit nicht.
Artikelverzeichnis
- 1 So lösen Sie Gleichungen ersten Grades
- 1.1 Grafische Interpretation
- 2 Beispiele für einfache lineare Gleichungen
- 2.1 Ganzzahlige Gleichungen
- 2.2 Bruchgleichungen
- 2.3 Wörtliche Gleichungen
- 2.4 Gleichungssysteme ersten Grades
- 2.5 Lineare Gleichungen mit Absolutwert
- 3 Einfache gelöste Übungen
- 3.1 - Übung 1
- 3.2 - Übung 2
- 3.3 - Übung 3
- 4 Referenzen
Wie man Gleichungen ersten Grades löst
Die Lösung einer Gleichung ersten Grades wird auch als Wurzel bezeichnet. Es ist der Wert von x, der den ursprünglichen Ausdruck in eine Gleichheit konvertiert. Zum Beispiel in:
5x = 8x - 15
Wenn wir in dieser Gleichung x = 5 einsetzen, erhalten wir:
5⋅5 = 8⋅5 - 15
25 = 40-15
25 = 25
Da lineare Gleichungen ersten Grades in vielen Formen vorliegen, die manchmal nicht offensichtlich sind, gibt es eine Reihe allgemeiner Regeln, die verschiedene algebraische Manipulationen umfassen, um den Wert des Unbekannten zu ermitteln:
-Wenn es Operationen gibt, sollten diese zunächst ausgeführt werden.
-Gruppierungssymbole wie Klammern, eckige Klammern und ggf. Klammern sollten entfernt werden, wobei die entsprechenden Zeichen zu beachten sind.
-Die Begriffe werden transponiert, um alle diejenigen, die das Unbekannte enthalten, auf die eine Seite der Gleichheit und diejenigen, die es nicht enthalten, auf die andere Seite zu stellen.
-Dann werden alle ähnlichen Begriffe reduziert, um zum Formular zu gelangen ax = -b.
-Und der letzte Schritt ist, das Unbekannte zu beseitigen.
Grafische Interpretation
Die zu Beginn angehobene Gleichung ersten Grades kann aus der Gleichung der Linie y = mx + c abgeleitet werden, wodurch y = 0 wird. Der resultierende Wert von x entspricht dem Schnittpunkt der Linie mit der horizontalen Achse.
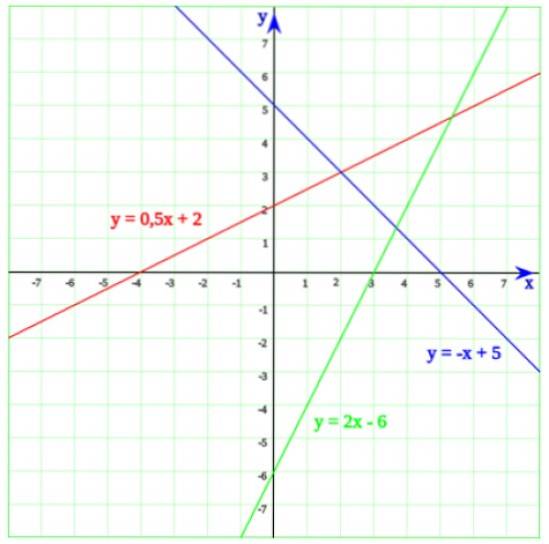
In der folgenden Abbildung gibt es drei Zeilen. Beginnend mit der grünen Linie, deren Gleichung lautet:
y = 2x - 6
Wenn y in der Gleichung der Linie y = 0 ist, erhält man die Gleichung ersten Grades:
2x - 6 = 0
Wessen Lösung ist x = 6/2 = 3. Wenn wir nun den Graphen detaillieren, ist es leicht zu erkennen, dass die Linie tatsächlich die horizontale Achse bei x = 3 schneidet.
Die blaue Linie schneidet die x-Achse bei x = 5, was die Lösung für die Gleichung -x + 5 = 0 ist. Schließlich schneidet die Linie, deren Gleichung y = 0,5x + 2 ist, die x-Achse bei x = - 4 , was aus der Gleichung ersten Grades leicht ersichtlich ist:
0,5 x + 2 = 0
x = 2 / 0,5 = 4
Beispiele für einfache lineare Gleichungen
Ganzzahlige Gleichungen
Dies sind diejenigen, in deren Begriffen es keine Nenner gibt, zum Beispiel:
21 - 6x = 27 - 8x
Ihre Lösung lautet:
-6x + 8x = 27 - 21
2x = 6
x = 3
Bruchgleichungen
Diese Gleichungen enthalten mindestens einen anderen Nenner als 1. Um sie zu lösen, ist es ratsam, alle Terme mit dem kleinsten gemeinsamen Vielfachen (LCM) der Nenner zu multiplizieren, um sie zu eliminieren.
Die folgende Gleichung ist ein Bruchtyp:

Da diese Zahlen klein sind, ist es nicht schwer zu erkennen, dass m.c.m (6, 8,12) = 24. Dieses Ergebnis wird leicht erhalten, indem die Zahlen als Produkt von Primzahlen oder ihren Potenzen ausgedrückt werden.
6 = 3,2
8 = 23
12 = 2zwei⋅3
Das kleinste gemeinsame Vielfache wird bestimmt, indem die gemeinsamen und ungewöhnlichen Faktoren 6, 8 und 12 mit ihrem größten Exponenten multipliziert werden. Dann:
lcm (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Da wir das kleinste gemeinsame Vielfache haben, muss es mit jedem der Terme der Gleichung multipliziert werden:

4 (x + 5) -3 (2x + 3) = 2 (1-5x)
Wir nutzen die Verteilungseigenschaft:
4x + 20 - 6x -9 = 2 - 10x
Alle Begriffe, die das unbekannte "x" enthalten, werden auf der linken Seite der Gleichheit gruppiert, wobei die unabhängigen oder numerischen Begriffe auf der rechten Seite verbleiben:
4x - 6x + 10 x = 2 + 9 - 20
8x = -9
x = - 9/8
Wörtliche Gleichungen
Es handelt sich um lineare Gleichungen mit einem Unbekannten, die jedoch von Literalkoeffizienten (Buchstaben) begleitet werden. Diese Buchstaben werden wie Zahlen behandelt. Ein Beispiel für eine wörtliche Gleichung ersten Grades ist:
-3ax + 2a = 5x - b
Diese Gleichung wird auf die gleiche Weise gelöst, als ob die unabhängigen Terme und Koeffizienten numerisch wären:
-3ax - 5x = - b - 2a
Faktorisierung des unbekannten "x":
x (-3a - 5) = - b - 2a
x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)
Gleichungssysteme ersten Grades
Gleichungssysteme bestehen aus einem Satz von Gleichungen mit zwei oder mehr Unbekannten. Die Lösung des Systems besteht aus Werten, die die Gleichungen gleichzeitig erfüllen, und um sie eindeutig zu bestimmen, muss für jedes Unbekannte eine Gleichung vorhanden sein.
Die allgemeine Form eines Systems von m lineare Gleichungen mit n Unbekannt ist:
zuelfx1 + zu12xzwei +… Zu1nxn = b1
zueinundzwanzigx1 + zu22xzwei +… Zu2nxn = bzwei
...
zum1x1 + zum2xzwei +… Zumnxn = bm
Wenn das System eine Lösung hat, heißt es kompatibel bestimmt, wenn es eine unendliche Menge von Werten gibt, die es erfüllen, ist es unbestimmt kompatibel, und schließlich, wenn es keine Lösung hat, dann ist es unvereinbar.
Bei der Lösung linearer Gleichungssysteme werden verschiedene Methoden verwendet: Reduktion, Substitution, Entzerrung, grafische Methoden, Gauß-Jordan-Eliminierung und die Verwendung von Determinanten gehören zu den am häufigsten verwendeten. Es gibt jedoch andere Algorithmen, um die Lösung zu erreichen, die für Systeme mit vielen Gleichungen und Unbekannten bequemer sind.
Ein Beispiel für ein lineares Gleichungssystem mit zwei Unbekannten ist:
8x - 5 = 7y - 9
6x = 3y + 6
Die Lösung dieses Systems wird später im Abschnitt über gelöste Übungen vorgestellt..
Lineare Gleichungen mit absolutem Wert
Der absolute Wert einer reellen Zahl ist der Abstand zwischen ihrer Position auf der Zahlenlinie und 0 auf der Zahlenlinie. Da es sich um eine Entfernung handelt, ist ihr Wert immer positiv.
Der Absolutwert einer Zahl wird durch die Modulobalken angegeben: │x│. Der absolute Wert einer positiven oder negativen Zahl ist immer positiv, zum Beispiel:
│ + 8│ = 8
│-3│ = 3
In einer Absolutwertgleichung liegt das Unbekannte zwischen Modulstäben. Betrachten wir die folgende einfache Gleichung:
│x│ = 10
Es gibt zwei Möglichkeiten, die erste ist, dass x eine positive Zahl ist. In diesem Fall haben wir:
x = 10
Und die andere Möglichkeit ist, dass x in diesem Fall eine negative Zahl ist:
x = -10
Dies sind die Lösungen dieser Gleichung. Schauen wir uns nun ein anderes Beispiel an:
│x + 6│ = 11
Die Menge innerhalb der Balken kann positiv sein, also:
x + 6 = 11
x = 11 -6 = 5
Oder es kann negativ sein. In diesem Fall:
-(x + 6) = 11
-x - 6 = 11 ⇒ -x = 11 + 6 = 17
Und der Wert des Unbekannten ist:
x = -17
Diese Absolutwertgleichung hat daher zwei Lösungen: x1 = 5 und xzwei = -17. Wir können überprüfen, ob beide Lösungen zu einer Gleichheit in der ursprünglichen Gleichung führen:
│5 + 6│ = 11
<11> = 11
Y.
17-17 + 6│ = 11
│-11│ = 11
Einfache gelöste Übungen
- Übung 1
Lösen Sie das folgende lineare Gleichungssystem mit zwei Unbekannten:
8x - 5 = 7y - 9
6x = 3y + 6
Lösung
Wie vorgeschlagen, ist dieses System ideal für die Verwendung der Substitutionsmethode, da in der zweiten Gleichung das Unbekannte x ist fast bereit für die Freigabe:
x = (3y + 6) / 6
Und es kann sofort in die erste Gleichung eingesetzt werden, die dann zu einer Gleichung ersten Grades mit unbekanntem "y" wird:
8 [(3y + 6) / 6] - 5 = 7y - 9
Der Nenner kann entfernt werden, indem jeder Term mit 6 multipliziert wird:
6. 8⋅ [(3y + 6) / 6] - 6,5 = 6,7y- 6. 9
8⋅ (3y + 6) - 30 = 42y - 54
Anwenden der Verteilungseigenschaft im ersten Term auf das Recht auf Gleichheit:
24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54
Die Gleichung kann vereinfacht werden, da alle Koeffizienten Vielfache von 6 sind:
4y + 3 = 7y - 9
-3y = -12
y = 4
Mit diesem Ergebnis gehen wir zum Löschen von x:
x = (3y + 6) / 6 → x = (12 + 6) / 6 = 3
- Übung 2
Löse die folgende Gleichung:
Lösung
Produkte erscheinen in dieser Gleichung und müssen gemäß den Anweisungen zu Beginn zuerst entwickelt werden:
3x - 10x +14 = 5x + 36x + 12
Dann werden alle Begriffe, die die Unbekannten enthalten, auf die linke Seite der Gleichheit gestellt, und auf der rechten Seite werden die unabhängigen Begriffe angezeigt:
3x - 10x - 5x - 36x = 12 - 14
-48x = -2
x = 1/24
- Übung 3
Das Hinzufügen der drei Innenwinkel eines Dreiecks ergibt 180º. Das Dur übersteigt das Moll um 35º, und das letztere übersteigt wiederum die Differenz zwischen Dur und Medium um 20º. Was sind die Winkel?
Lösung
Wir nennen "x" den größeren Winkel, "y" den mittleren und "z" den kleinsten. Wenn die Aussage bestätigt, dass die Summe von ihnen 180º beträgt, kann geschrieben werden:
x + y + z = 180
Dann wissen wir, dass das Größere das Kleinere um 35º übersteigt. Wir können dies so schreiben:
x = z + 35
Schließlich übersteigt der kleinste die Differenz zwischen dem größten und dem mittleren um 20 °:
z = x - y + 20
Wir haben ein System von 3 Gleichungen und 3 Unbekannten:
x + y + z = 180
x = z + 35
z = x - y + 20
Auflösen nach z aus der ersten Gleichung, die wir haben:
z = 180 - x - y
Passend zum dritten:
180 - x - y = x - y + 20
Die Unbekannten wie immer an die linke Seite weitergeben:
-x - y - x + y = 20 - 180
Das "y" wird gelöscht und bleibt:
-2x = - 160
x = 80º
Aus der zweiten Gleichung ergibt sich der Wert von z:
z = x - 35 = 80 - 35 = 45º
Und der Wert von y ergibt sich aus dem ersten oder dritten:
y = 180 - x - z = 180 - 80 - 45 = 55º
Verweise
- Baldor. 1977. Elementare Algebra. Venezolanische Kulturausgaben.
- Monterey Institute. Gleichungen, Ungleichungen und absoluter Wert. Wiederhergestellt von: montereyinstitute.org.
- Online-Lehrer. Klassifikation von linearen Gleichungen oder Gleichungen ersten Grades. Wiederhergestellt von: profesorenlinea.cl.
- Hoffman, J. Auswahl mathematischer Themen. Band 2.
- Jiménez, R. 2008. Algebra. Prentice Halle.
- Zill, D. 1984. Algebra und Trigonometrie. Mcgraw Hügel.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.