
Verteilung F Eigenschaften und Übungen gelöst
Das F-Verteilung o Die Fisher-Snedecor-Verteilung wird verwendet, um die Varianzen zweier verschiedener oder unabhängiger Populationen zu vergleichen, von denen jede einer Normalverteilung folgt.
Die Verteilung, die der Varianz eines Satzes von Stichproben aus einer einzelnen Normalpopulation folgt, ist die Chi-Quadrat-Verteilung (Χzwei) vom Grad n-1, wenn jede der Abtastungen in der Menge n Elemente hat.
Um die Varianzen zweier verschiedener Populationen zu vergleichen, muss a definiert werden statistisch, Dies ist eine zusätzliche Zufallsvariable, mit der wir erkennen können, ob beide Populationen dieselbe Varianz aufweisen oder nicht.
Diese Hilfsvariable kann direkt der Quotient der Stichprobenvarianzen jeder Population sein. In diesem Fall gibt es Hinweise darauf, dass beide Populationen ähnliche Varianzen aufweisen, wenn dieser Quotient nahe an der Einheit liegt.
Artikelverzeichnis
- 1 Die F-Statistik und ihre theoretische Verteilung
- 1.1 Mittelwert, Modus und Varianz der F-Verteilung
- 2 Umgang mit der F-Verteilung
- 2.1 Tabellen der F-Verteilung
- 2.2 Software für die F-Verteilung
- 3 Gelöste Übungen
- 3.1 Übung 1
- 3.2 Übung 2
- 4 Referenzen
Die F-Statistik und ihre theoretische Verteilung
Die von Ronald Fisher (1890 - 1962) vorgeschlagene Zufallsvariablen-F- oder F-Statistik wird am häufigsten zum Vergleich der Varianzen zweier Populationen verwendet und ist wie folgt definiert:
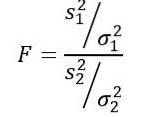
Sein szwei die Stichprobenvarianz und σzwei die Populationsvarianz. Zur Unterscheidung jeder der beiden Bevölkerungsgruppen werden die Indizes 1 bzw. 2 verwendet..
Es ist bekannt, dass die Chi-Quadrat-Verteilung mit (n-1) Freiheitsgraden diejenige ist, die der nachstehend definierten Hilfsvariablen (oder statistischen Variablen) folgt:
X.zwei = (n-1) szwei / σzwei.
Daher folgt die F-Statistik einer theoretischen Verteilung, die durch die folgende Formel gegeben ist:
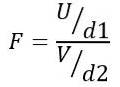
Sein ODER die Chi-Quadrat-Verteilung mit d1 = n1 - 1 Freiheitsgrade für Bevölkerung 1 und V. die Chi-Quadrat-Verteilung mit d2 = n2 - 1 Freiheitsgrade für die Bevölkerung 2.
Der auf diese Weise definierte Quotient ist eine neue Wahrscheinlichkeitsverteilung, bekannt als F-Verteilung mit d1 Freiheitsgrade im Zähler und d2 Freiheitsgrade im Nenner.
Mittelwert, Modus und Varianz der F-Verteilung
Hälfte
Der Mittelwert der F-Verteilung wird wie folgt berechnet:
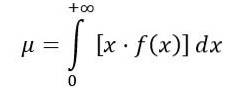
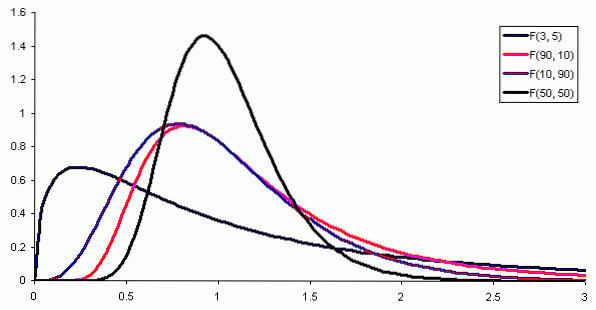
Dabei ist f (x) die Wahrscheinlichkeitsdichte der F-Verteilung, die in Abbildung 1 für verschiedene Kombinationen von Parametern oder Freiheitsgraden dargestellt ist.
Wir können die Wahrscheinlichkeitsdichte f (x) als Funktion der Funktion Γ (Gammafunktion) schreiben:
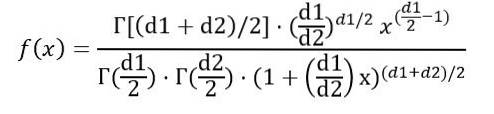
Sobald das oben angegebene Integral ausgeführt wurde, wird geschlossen, dass der Mittelwert der F-Verteilung mit Freiheitsgraden (d1, d2) ist:
μ = d2 / (d2 - 2) mit d2> 2
Wo angemerkt wird, dass der Mittelwert seltsamerweise nicht von den Freiheitsgraden d1 des Zählers abhängt.
Mode
Andererseits hängt der Modus von d1 und d2 ab und ist gegeben durch:
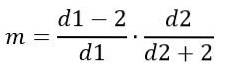
Für d1> 2.
Varianz der F-Verteilung
Die Varianz σzwei der F-Verteilung wird aus dem Integral berechnet:
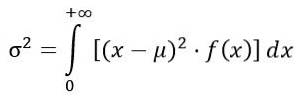
Erhalten:
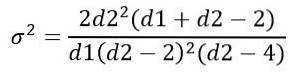
Umgang mit der F-Verteilung
Wie bei anderen kontinuierlichen Wahrscheinlichkeitsverteilungen, die komplizierte Funktionen beinhalten, erfolgt die Behandlung der F-Verteilung mithilfe von Tabellen oder Software..
Verteilungstabellen F.
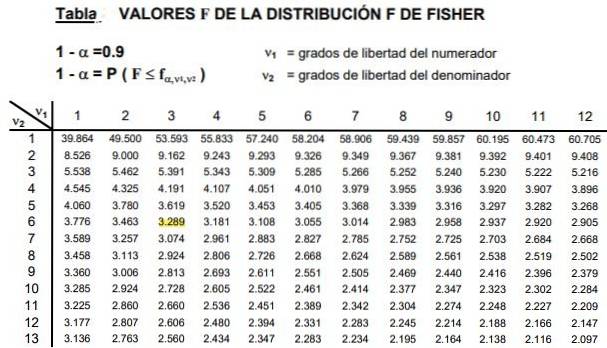
Die Tabellen enthalten die beiden Parameter oder Freiheitsgrade der F-Verteilung, die Spalte gibt den Freiheitsgrad des Zählers und die Zeile den Freiheitsgrad des Nenners an.
Abbildung 2 zeigt einen Ausschnitt aus der Tabelle der F-Verteilung für den Fall von a Signifikanzniveau von 10%, das ist α = 0,1. Der Wert von F wird hervorgehoben, wenn d1 = 3 und d2 = 6 mit Konfidenzniveau 1- & agr; = 0,9, das sind 90%.
Software für die F-Verteilung
Was die Software betrifft, die die F-Verteilung handhabt, gibt es eine große Vielfalt von Tabellenkalkulationen wie z Excel zu spezialisierten Paketen wie Minitab, SPSS Y. R. um einige der bekanntesten zu nennen.
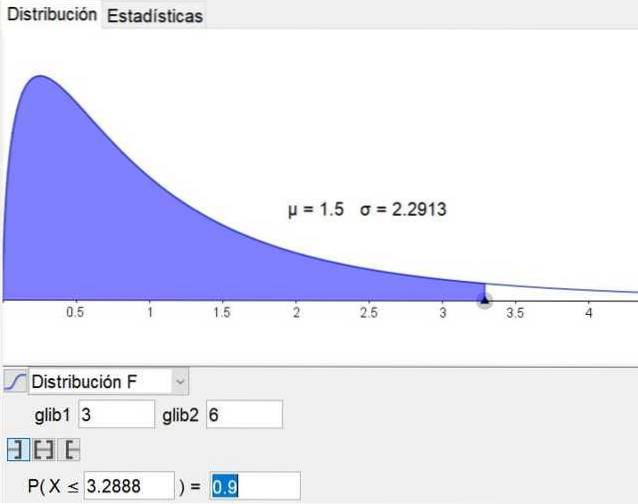
Es ist bemerkenswert, dass die Geometrie- und Mathematik-Software Geogebra verfügt über ein statistisches Tool, das die Hauptverteilungen einschließlich der F-Verteilung enthält. Abbildung 3 zeigt die F-Verteilung für den Fall d1 = 3 und d2 = 6 mit Konfidenzniveau von 90%.
Gelöste Übungen
Übung 1
Betrachten Sie zwei Stichproben von Populationen mit derselben Populationsvarianz. Wenn Probe 1 die Größe n1 = 5 und Probe 2 die Größe n2 = 10 hat, bestimmen Sie die theoretische Wahrscheinlichkeit, dass der Quotient ihrer jeweiligen Varianzen kleiner oder gleich 2 ist.
Lösung
Es ist zu beachten, dass die F-Statistik wie folgt definiert ist:
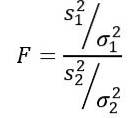
Uns wird jedoch gesagt, dass die Populationsabweichungen gleich sind. Für diese Übung gilt Folgendes:
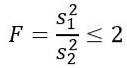
Da wir die theoretische Wahrscheinlichkeit kennen wollen, dass dieser Quotient aus Stichprobenvarianzen kleiner oder gleich 2 ist, müssen wir den Bereich unter der F-Verteilung zwischen 0 und 2 kennen, der durch Tabellen oder Software erhalten werden kann. Dabei ist zu berücksichtigen, dass die erforderliche F-Verteilung d1 = n1 - 1 = 5 - 1 = 4 und d2 = n2 - 1 = 10 - 1 = 9 hat, dh die F-Verteilung mit Freiheitsgraden ( 4, 9).
Mit dem statistischen Tool von Geogebra Es wurde festgestellt, dass dieser Bereich 0,82 beträgt, sodass der Schluss gezogen wird, dass die Wahrscheinlichkeit, dass der Quotient der Stichprobenvarianzen kleiner oder gleich 2 ist, 82% beträgt.
Übung zwei
Es gibt zwei Herstellungsverfahren für dünne Bleche. Die Variabilität der Dicke sollte so gering wie möglich sein. Aus jedem Prozess werden 21 Proben entnommen. Die Probe aus Prozess A hat eine Standardabweichung von 1,96 Mikron, während die Probe aus Prozess B eine Standardabweichung von 2,13 Mikron hat. Welcher der Prozesse weist die geringste Variabilität auf? Verwenden Sie eine Ablehnungsstufe von 5%.
Lösung
Die Daten sind wie folgt: Sb = 2,13 mit nb = 21; Sa = 1,96 mit na = 21. Dies bedeutet, dass wir mit einer F-Verteilung von (20, 20) Freiheitsgraden arbeiten müssen.
Die Nullhypothese impliziert, dass die Populationsvarianz beider Prozesse identisch ist, dh σa ^ 2 / σb ^ 2 = 1. Die alternative Hypothese würde unterschiedliche Populationsvarianzen implizieren.
Dann wird unter der Annahme identischer Populationsvarianzen die berechnete F-Statistik definiert als: Fc = (Sb / Sa) ^ 2.
Da das Ablehnungsniveau als α = 0,05 angenommen wurde, ist α / 2 = 0,025
Die Verteilung F (0,025, 20,20) = 0,406, während F (0,975, 20,20) = 2,46.
Daher ist die Nullhypothese wahr, wenn das berechnete F erfüllt: 0,406 ≤ Fc ≤ 2,46. Andernfalls wird die Nullhypothese verworfen.
Da Fc = (2.13 / 1.96) ^ 2 = 1.18 ist, wird der Schluss gezogen, dass die Fc-Statistik mit einer Sicherheit von 95% im Akzeptanzbereich der Nullhypothese liegt. Mit anderen Worten, mit 95% iger Sicherheit weisen beide Herstellungsverfahren die gleiche Populationsvarianz auf..
Verweise
- F Unabhängigkeitstest. Wiederhergestellt von: saylordotorg.github.io.
- Med Wave. Statistik für die Gesundheitswissenschaften: der F-Test. Abgerufen von: medwave.cl.
- Wahrscheinlichkeiten und Statistiken. Verteilung F. Wiederhergestellt von: probayestadistica.com.
- Triola, M. 2012. Elementare Statistik. 11 .. Auflage. Addison Wesley.
- UNAM. Verteilung F. Wiederhergestellt von: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Verbreitung F. Wiederhergestellt von: es.wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.