Das additive Zersetzung einer positiven ganzen Zahl ist es, sie als Summe von zwei oder mehr positiven ganzen Zahlen auszudrücken. Wir haben also, dass die Zahl 5 ausgedrückt werden kann als 5 = 1 + 4, 5 = 2 + 3 oder 5 = 1 + 2 + 2. Jede dieser Schreibweisen der Zahl 5 wird als additive Zerlegung bezeichnet.
Wenn wir darauf achten, können wir sehen, dass die Ausdrücke 5 = 2 + 3 und 5 = 3 + 2 dieselbe Zusammensetzung darstellen; beide haben die gleichen Nummern. Der Einfachheit halber wird jedoch jeder der Addends normalerweise nach dem Kriterium vom niedrigsten zum höchsten geschrieben.
Artikelverzeichnis
Als weiteres Beispiel können wir die Nummer 27 nehmen, die wir ausdrücken können als:
27 = 7 + 10 + 10
27 = 9 + 9 + 9
27 = 3 + 6 + 9 + 9
27 = 9 + 18
Die additive Zerlegung ist ein sehr nützliches Werkzeug, mit dem wir unser Wissen über Nummerierungssysteme vertiefen können.
Wenn wir Zahlen mit mehr als zwei Ziffern haben, besteht eine besondere Art, sie zu zerlegen, in den Vielfachen von 10, 100, 1000, 10 000 usw., aus denen sie bestehen. Diese Art, eine beliebige Zahl zu schreiben, wird als kanonische additive Zerlegung bezeichnet. Zum Beispiel kann die Nummer 1456 wie folgt zerlegt werden:
1456 = 1000 + 400+ 50 + 6
Wenn wir die Nummer 20 846 295 haben, lautet ihre kanonische additive Zersetzung:
20 846 295 = 20.000.000 + 800.000 + 40.000 + 6000 + 200 + 90 +5.
Dank dieser Zerlegung können wir sehen, dass der Wert einer bestimmten Ziffer durch die Position gegeben ist, die sie einnimmt. Nehmen wir als Beispiel die Zahlen 24 und 42:
24 = 20 + 4
42 = 40 +2
Hier können wir sehen, dass in 24 die 2 einen Wert von 20 Einheiten und die 4 einen Wert von 4 Einheiten hat; Andererseits hat die 4 in 42 einen Wert von 40 Einheiten und die 2 von zwei Einheiten. Obwohl beide Zahlen die gleichen Ziffern verwenden, sind ihre Werte aufgrund der Position, die sie einnehmen, völlig unterschiedlich.
Eine der Anwendungen, die wir der additiven Zerlegung geben können, sind bestimmte Arten von Beweisen, bei denen es sehr nützlich ist, eine positive ganze Zahl als die Summe anderer zu sehen.
Nehmen wir als Beispiel den folgenden Satz mit seinen jeweiligen Beweisen.
- Sei Z eine 4-stellige ganze Zahl, dann ist Z durch 5 teilbar, wenn seine Einheitennummer Null oder fünf ist.
Erinnern wir uns, was Teilbarkeit ist. Wenn wir "a" und "b" ganze Zahlen haben, sagen wir, dass "a" "b" teilt, wenn es eine ganze Zahl "c" gibt, so dass b = a * c.
Eine der Eigenschaften der Teilbarkeit besagt, dass, wenn „a“ und „b“ durch „c“ teilbar sind, die Subtraktion „a-b“ ebenfalls teilbar ist..
Sei Z eine 4-stellige ganze Zahl; deshalb können wir Z als Z = ABCD schreiben.
Unter Verwendung der kanonischen additiven Zersetzung haben wir:
Z = A * 1000 + B * 100 + C * 10 + D.
Es ist klar, dass A * 1000 + B * 100 + C * 10 durch 5 teilbar ist. Aus diesem Grund haben wir, dass Z durch 5 teilbar ist, wenn Z - (A * 1000 + B * 100 + C * 10) durch teilbar ist 5.
Aber Z - (A * 1000 + B * 100 + C * 10) = D und D ist eine einstellige Zahl. Die einzige Möglichkeit, durch 5 teilbar zu sein, besteht darin, 0 oder 5 zu sein.
Daher ist Z durch 5 teilbar, wenn D = 0 oder D = 5 ist.
Beachten Sie, dass wenn Z n Ziffern hat, der Beweis genau der gleiche ist, es sich nur ändert, dass wir jetzt Z = A schreiben würden1ZUzwei… ZUn und das Ziel wäre zu beweisen, dass A.n Es ist null oder fünf.
Wir sagen, dass eine Partition einer positiven Ganzzahl eine Möglichkeit ist, eine Zahl als Summe positiver Ganzzahlen zu schreiben.
Der Unterschied zwischen einer additiven Zerlegung und einer Partition besteht darin, dass die Partition diese Einschränkung nicht hat, während die erste versucht, dass sie zumindest in zwei oder mehr Addenden zerlegt werden kann.
Somit haben wir folgendes:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 2 + 2
Die oben genannten sind Partitionen von 5.
Das heißt, wir haben, dass jede additive Zerlegung eine Partition ist, aber nicht jede Partition ist notwendigerweise eine additive Zerlegung..
In der Zahlentheorie garantiert der Grundsatz der Arithmetik, dass jede ganze Zahl als Produkt von Primzahlen eindeutig geschrieben werden kann.
Beim Studium von Partitionen besteht das Ziel darin, zu bestimmen, auf wie viele Arten eine positive Ganzzahl als Summe anderer Ganzzahlen geschrieben werden kann. Daher definieren wir die Partitionsfunktion wie unten dargestellt.
Die Partitionsfunktion p (n) ist definiert als die Anzahl der Möglichkeiten, wie eine positive ganze Zahl n als Summe positiver ganzer Zahlen geschrieben werden kann.
Zurück zum Beispiel von 5, wir haben das:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1
Somit ist p (5) = 7.
Sowohl Partitionen als auch additive Zerlegungen einer Zahl n können geometrisch dargestellt werden. Angenommen, wir haben eine additive Zerlegung von n. Bei dieser Zerlegung können die Addenden so angeordnet werden, dass die Mitglieder der Summe vom kleinsten zum größten geordnet sind. So okay:
n = a1 + zuzwei + zu3 +… + A.r mit
zu1 ≤ azwei ≤ a3 ≤… ≤ ar.
Wir können diese Zerlegung folgendermaßen grafisch darstellen: In einer ersten Zeile markieren wir das a1-Punkte, dann markieren wir im nächstenzwei-Punkte und so weiter bis zum Erreichen von ar.
Nehmen Sie zum Beispiel die Zahl 23 und ihre folgende Zerlegung:
23 = 5 + 4 + 7 + 3 + 1 + 3
Wir ordnen diese Zerlegung an und haben:
23 = 1 + 3 + 3 + 4+ 5 + 7
Das entsprechende Diagramm wäre:
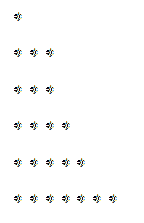
Wenn wir diesen Graphen vertikal statt horizontal lesen, können wir ebenfalls eine Zerlegung erhalten, die sich möglicherweise von der vorherigen unterscheidet. Im Beispiel von 23 fällt Folgendes auf:
Wir haben also 23, wir können es auch schreiben als:
23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.