
Ableitung der Kotangensberechnung, Beweis, Übungen
Das Derivat des Kotangens ist gleich dem Gegenteil des Quadrats des Kosekanten "-Csczwei”. Diese Formel folgt per Definition den Gesetzen der Ableitung und der Differenzierung trigonometrischer Funktionen. Es wird wie folgt bezeichnet:
d (ctg u) = -csczwei oder . du
Wobei "du" den von der Argumentfunktion abgeleiteten Ausdruck in Bezug auf die unabhängige Variable symbolisiert.

Artikelverzeichnis
- 1 Wie wird es berechnet??
- 2 Eigenschaften der Kotangensfunktion
- 2.1 Vertikale Asymptoten
- 2.2 Domain
- 2.3 Reichweite
- 2.4 Frequenz
- 2.5 Verhalten
- 3 Demo
- 3.1 Trigonometrischer Differentialnachweis
- 3.2 Beweis per Definition des Derivats
- 4 Gelöste Übungen
- 4.1 Übung 1
- 4.2 Übung 2
- 5 Referenzen
Wie wird es berechnet??
Das Verfahren zur Entwicklung dieser Derivate ist recht einfach. Sie müssen lediglich das Argument und die Art der Funktion, die es darstellt, korrekt identifizieren..
Zum Beispiel hat der Ausdruck Ctg (f / g) eine Unterteilung in seinem Argument. Dies erfordert eine Differenzierung in Bezug auf U / V nach der Entwicklung der Ableitung des Kotangens.
Der Kotangens ist der Kehrwert der Tangente. Algebraisch bedeutet dies, dass:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Es ist falsch zu sagen, dass die Kotangensfunktion die "Umkehrung" der Tangente ist. Dies liegt daran, dass die inverse Tangentenfunktion per Definition eine Bogen-Tangente ist.
(Tg-1 x) = arctg x
Nach der pythagoreischen Trigonometrie ist der Kotangens an folgenden Abschnitten beteiligt:
Ctg x = (cos x) / (sin x)
Ctgzwei x + 1 = Csczwei x
Laut analytischer Trigonometrie reagiert es auf folgende Identitäten:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgzwei a) / (2tg a)
Eigenschaften der Kotangensfunktion
Es ist notwendig, verschiedene Eigenschaften der Funktion f (x) = ctg x zu analysieren, um die Aspekte zu definieren, die zur Untersuchung ihrer Differenzierbarkeit und Anwendung erforderlich sind.
Vertikale Asymptoten
Die Kotangensfunktion ist nicht für die Werte definiert, die den Ausdruck "Senx" zu Null machen. Aufgrund seines Äquivalents Ctg x = (cos x) / (sin x) hat es eine Unbestimmtheit in allen "nπ", wobei n zu den ganzen Zahlen gehört.
Das heißt, in jedem dieser Werte von x = nπ gibt es eine vertikale Asymptote. Wenn Sie sich von links nähern, nimmt der Wert des Kotangens schnell ab, und wenn Sie sich von rechts nähern, nimmt die Funktion auf unbestimmte Zeit zu.
Domain
Die Domäne der Kotangensfunktion wird durch die Menge x ∈ R / x ≠ nπ, n ∈ Z ausgedrückt. Dies wird gelesen als "x, das zu der Menge von reellen Zahlen gehört, so dass x von nπ verschieden ist, wobei n zu der Menge von ganzen Zahlen gehört".
Rang
Der Bereich der Kotangensfunktion reicht von minus bis plus unendlich. Daraus kann geschlossen werden, dass sein Bereich die Menge der reellen Zahlen R ist.
Frequenz
Die Kotangensfunktion ist periodisch und ihre Periode ist gleich π. Auf diese Weise wird die Gleichheit Ctg x = Ctg (x + nπ) erfüllt, wobei n zu Z gehört.
Verhalten
Es ist eine ungerade Funktion, da Ctg (-x) = - Ctg x. Auf diese Weise ist bekannt, dass die Funktion eine Symmetrie in Bezug auf den Koordinatenursprung aufweist. Es zeigt auch eine Abnahme in jedem Intervall zwischen zwei aufeinanderfolgenden vertikalen Asymptoten.
Es hat keine Maximal- oder Minimalwerte, da seine Annäherungen an die vertikalen Asymptoten Verhaltensweisen aufweisen, bei denen die Funktion unbegrenzt zunimmt oder abnimmt.
Die Nullen oder Wurzeln der Kotangensfunktion werden bei ungeraden Vielfachen von π / 2 gefunden. Dies bedeutet, dass Ctg x = 0 für Werte der Form x = nπ / 2 mit n ungeraden ganzen Zahlen gilt.
Demonstration
Es gibt zwei Möglichkeiten, die Ableitung der Kotangensfunktion zu beweisen.
Trigonometrischer Differentialnachweis
Die Ableitung der Kotangensfunktion von ihrem Äquivalent in Sinus und Cosinus ist bewiesen.
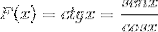
Es wird als Ableitung einer Funktionsteilung behandelt
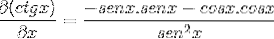
Nach der Ableitung werden die Faktoren gruppiert und das Ziel ist es, die pythagoreischen Identitäten zu emulieren
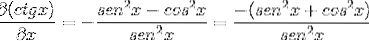
Durch Ersetzen der Identitäten und Anwenden der Reziprozität wird der Ausdruck erhalten
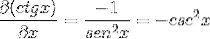
Beweis per Definition der Ableitung
Der folgende Ausdruck entspricht per Definition der Ableitung. Wobei sich der Abstand zwischen 2 Punkten der Funktion Null nähert.
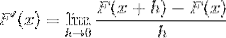
Wir ersetzen den Kotangens, den wir haben:
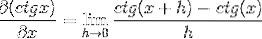
Identitäten werden für die Summe von Argumenten und Reziprozität angewendet
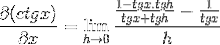
Der Bruchteil des Zählers wird traditionell betrieben
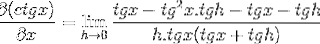
Wenn wir die entgegengesetzten Elemente eliminieren und einen gemeinsamen Faktor verwenden, erhalten wir
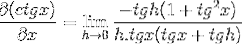
Wir müssen pythagoreische Identitäten und Gegenseitigkeit anwenden
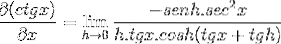
Die in x ausgewerteten Elemente sind in Bezug auf die Grenze konstant, daher können sie das Argument dafür verlassen. Dann werden Eigenschaften von trigonometrischen Grenzen angewendet.
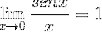
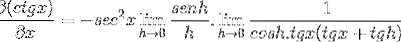
Das Limit wird ausgewertet
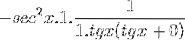
Dann wird berücksichtigt, bis der gewünschte Wert erreicht ist
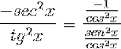
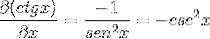
Die Ableitung des Kotangens wird somit als das Gegenteil des Quadrats des Kosekanten gezeigt.
Gelöste Übungen
Übung 1
Definieren Sie basierend auf der Funktion f (x) den Ausdruck f '(x)
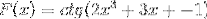
Die entsprechende Ableitung wird unter Beachtung der Kettenregel angewendet
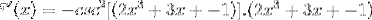
Das Argument ableiten
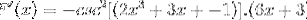
Manchmal ist es notwendig, wechselseitige oder trigonometrische Identitäten anzuwenden, um die Lösungen anzupassen.
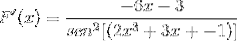
Übung 2
Definieren Sie den Differentialausdruck entsprechend F (x)
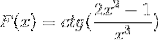
Nach der Ableitungsformel und unter Beachtung der Kettenregel
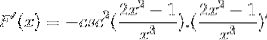
Das Argument wird abgeleitet, während der Rest gleich bleibt
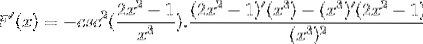
Ableiten aller Elemente
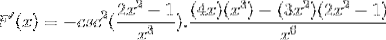
Traditionell arbeiten die Produkte der gleichen Basis
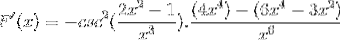
Die gleichen Elemente werden addiert und der gemeinsame Faktor wird extrahiert
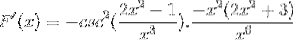
Schilder werden vereinfacht und bedient. Weg zum vollständig abgeleiteten Ausdruck
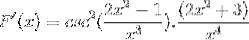
Verweise
- Trigonometrische Reihe, Band 1. A. Zygmund. Cambridge University Press, 2002
- Berechnung einer einzelnen Variablen. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. November 2008
- Kalkül mit Trigonometrie und analytischer Geometrie. John H. Saxon, John Saxon, Frank Wang und Diana Harvey. Saxon Publishers, 1988
- Multivariable Analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. Dezember. 2010
- Systemdynamik: Modellierung, Simulation und Steuerung von mechatronischen Systemen. Dekan C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. März 2012
- Kalkül: Mathematik und Modellierung. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. Januar 1999



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.