
Gepoolte Datenbeispiele und Übung gelöst
Das gruppierte Daten sind solche, die in Kategorien oder Klassen eingeteilt wurden, wobei ihre Häufigkeit als Kriterium herangezogen wurde. Dies geschieht, um den Umgang mit großen Datenmengen zu vereinfachen und deren Trends zu ermitteln..
Sobald die Daten nach ihren Häufigkeiten in diese Klassen eingeteilt sind, bilden sie a Häufigkeitsverteilung, aus denen nützliche Informationen durch ihre Eigenschaften extrahiert werden.

Hier ist ein einfaches Beispiel für gruppierte Daten:
Angenommen, die Größe von 100 Studentinnen, die aus allen grundlegenden Physikkursen einer Universität ausgewählt wurden, wird gemessen und die folgenden Ergebnisse erhalten:

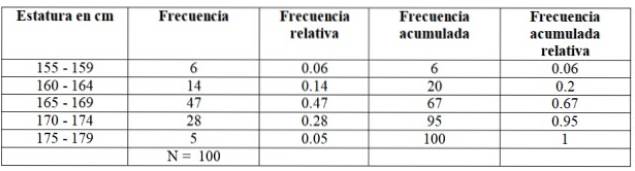
Die erhaltenen Ergebnisse wurden in 5 Klassen unterteilt, die in der linken Spalte erscheinen.
Die erste Klasse zwischen 155 und 159 cm hat 6 Schüler, die zweite Klasse zwischen 160 und 164 cm hat 14 Schüler, die dritte Klasse mit 165 bis 169 cm hat die meisten Mitglieder: 47. Dann geht die Klasse zwischen 170 und 174 cm weiter mit 28 Schülern und schließlich die 175-174 cm mit nur 5.
Die Anzahl der Mitglieder jeder Klasse ist genau die Frequenz oder Absolute Häufigkeit und wenn alle addiert werden, werden die Gesamtdaten erhalten, die in diesem Beispiel 100 sind.
Artikelverzeichnis
- 1 Eigenschaften der Häufigkeitsverteilung
- 1.1 Frequenz
- 1.2 Grenzen
- 1.3 Grenzen
- 1.4 Amplitude
- 1.5 Klassennote
- 2 Messungen der zentralen Tendenz und Streuung für gruppierte Daten
- 2.1 Durchschnitt
- 2.2 Median
- 2.3 Mode
- 2.4 Abweichung und Standardabweichung
- 3 Übung gelöst
- 3.1 Lösung a
- 3.2 Lösung b
- 3.3 Lösung d
- 4 Referenzen
Eigenschaften der Häufigkeitsverteilung
Frequenz
Wie wir gesehen haben, gibt die Häufigkeit an, wie oft ein Datenelement wiederholt wird. Um die Berechnung der Eigenschaften der Verteilung wie Mittelwert und Varianz zu erleichtern, werden folgende Größen definiert:
-Kumulative Häufigkeit: wird erhalten, indem die Frequenz einer Klasse mit der zuvor akkumulierten Frequenz addiert wird. Die erste aller Frequenzen entspricht der des betreffenden Intervalls, und die letzte ist die Gesamtzahl der Daten.
-Relative Frequenz: berechnet durch Teilen der absoluten Häufigkeit jeder Klasse durch die Gesamtzahl der Daten. Und wenn Sie mit 100 multiplizieren, haben Sie die relative prozentuale Häufigkeit.
-Kumulative relative Häufigkeit: ist die Summe der relativen Häufigkeiten jeder Klasse mit der zuvor akkumulierten. Die letzte der akkumulierten relativen Frequenzen muss gleich 1 sein.
In unserem Beispiel sehen die Frequenzen folgendermaßen aus:
Grenzen
Die Extremwerte jeder Klasse oder jedes Intervalls werden aufgerufen Klassengrenzen. Wie wir sehen können, hat jede Klasse eine untere und eine obere Grenze. Zum Beispiel hat die erste Klasse in der Studie über Höhen eine Untergrenze von 155 cm und eine Obergrenze von 159 cm..
In diesem Beispiel gibt es Grenzen, die klar definiert sind. Es ist jedoch möglich, offene Grenzen zu definieren: Wenn Sie nicht die genauen Werte definieren, sagen Sie "Höhe weniger als 160 cm", "Höhe weniger als 165 cm" und so weiter.
Grenzen
Die Höhe ist eine stetige Variable, daher kann davon ausgegangen werden, dass die erste Klasse tatsächlich bei 154,5 cm beginnt, da das Runden dieses Werts auf die nächste Ganzzahl 155 cm ergibt.
Diese Klasse deckt alle Werte bis 159,5 cm ab, da danach die Höhen auf 160,0 cm gerundet werden. Eine Höhe von 159,7 cm gehört bereits zur folgenden Klasse.
Die tatsächlichen Klassengrenzen für dieses Beispiel sind in cm:
- 154,5 - 159,5
- 159,5 - 164,5
- 164,5 - 169,5
- 169,5 - 174,5
- 174,5 - 179,5
Amplitude
Die Breite einer Klasse wird durch Subtrahieren der Grenzen erhalten. Für das erste Intervall unseres Beispiels haben wir 159,5 - 154,5 cm = 5 cm.
Der Leser kann überprüfen, ob für die anderen Intervalle des Beispiels die Amplitude ebenfalls 5 cm beträgt. Es ist jedoch zu beachten, dass Verteilungen mit Intervallen unterschiedlicher Amplitude konstruiert werden können.
Klassenzeichen
Es ist der Mittelpunkt des Intervalls und wird durch den Durchschnitt zwischen der Obergrenze und der Untergrenze erhalten.
In unserem Beispiel ist die erste Klassenmarke (155 + 159) / 2 = 157 cm. Der Leser kann sehen, dass die verbleibenden Klassenmarken sind: 162, 167, 172 und 177 cm.
Die Bestimmung der Klassenmarken ist wichtig, da sie erforderlich sind, um das arithmetische Mittel und die Varianz der Verteilung zu ermitteln.
Messungen der zentralen Tendenz und Streuung für gepoolte Daten
Die am häufigsten verwendeten Maße für die zentrale Tendenz sind der Mittelwert, der Median und der Modus. Sie beschreiben genau die Tendenz der Daten, sich um einen bestimmten zentralen Wert zu gruppieren..
Hälfte
Es ist eine der Hauptmaßnahmen der zentralen Tendenz. In den gruppierten Daten kann das arithmetische Mittel mit folgender Formel berechnet werden:

-X ist der Mittelwert
-F.ich ist die Häufigkeit der Klasse
-mich ist die Klassenmarke
-g ist die Anzahl der Klassen
-n ist die Gesamtzahl der Daten
Median
Für den Median muss das Intervall angegeben werden, in dem die Beobachtung n / 2 gefunden wird. In unserem Beispiel ist diese Beobachtung die Nummer 50, da insgesamt 100 Datenpunkte vorhanden sind. Diese Beobachtung liegt im Bereich von 165 bis 169 cm.
Dann müssen Sie interpolieren, um den numerischen Wert zu finden, der dieser Beobachtung entspricht, für die die Formel verwendet wird:

Wo:
-c = Breite des Intervalls, in dem der Median gefunden wird
-B.M. = die Untergrenze des Intervalls, zu dem der Median gehört
-F.m = Anzahl der im Medianintervall enthaltenen Beobachtungen
-n / 2 = die Hälfte aller Daten
-F.BM = Gesamtzahl der Beobachtungen Vor Medianintervall
Mode
Für den Modus wird die Modalklasse identifiziert, die die meisten Beobachtungen enthält und deren Klassenmarkierung bekannt ist.
Varianz und Standardabweichung
Die Varianz und die Standardabweichung sind Dispersionsmaße. Wenn wir die Varianz mit s bezeichnenzwei und die Standardabweichung, die die Quadratwurzel der Varianz als s ist, für gruppierte Daten haben wir jeweils:

Y.

Übung gelöst
Berechnen Sie für die zu Beginn vorgeschlagene Höhenverteilung der Studentinnen die Werte von:
a) Durchschnitt
b) Median
c) Mode
d) Varianz und Standardabweichung.

Lösung für
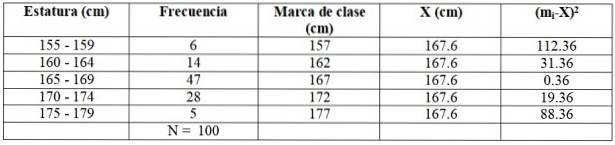
Erstellen wir die folgende Tabelle, um die Berechnungen zu vereinfachen:


Werte ersetzen und Summation direkt durchführen:
X = (6 × 157 + 14 × 162 + 47 × 167 + 28 × 172 + 5 × 177) / 100 cm =
= 167,6 cm
Lösung b
Das Intervall, zu dem der Median gehört, beträgt 165-169 cm, da es das Intervall mit der höchsten Frequenz ist.

Lassen Sie uns jeden dieser Werte im Beispiel anhand von Tabelle 2 identifizieren:
c = 5 cm (siehe Abschnitt Amplitude)
B.M. = 164,5 cm
F.m = 47
n / 2 = 100/2 = 50
F.BM = 20
Einsetzen in die Formel:
Das Intervall, das die meisten Beobachtungen enthält, beträgt 165-169 cm, dessen Klassenmarkierung 167 cm beträgt.
Lösung d
Wir erweitern die vorherige Tabelle um zwei zusätzliche Spalten:

Wir wenden die Formel an:

Und wir entwickeln die Summe:
szwei = (6 × 112,36 + 14 × 31,36 + 47 × 0,36 + 28 × 19,36 + 5 × 88,36) / 99 = = 21,35 cmzwei
Deshalb:
s = 21,35 cmzwei = 4,6 cm
Verweise
- Berenson, M. 1985. Statistik für Management und Wirtschaft. Interamericana S.A..
- Canavos, G. 1988. Wahrscheinlichkeit und Statistik: Anwendungen und Methoden. Mcgraw Hügel.
- Devore, J. 2012. Wahrscheinlichkeit und Statistik für Ingenieurwesen und Wissenschaft. 8 .. Auflage. Engagieren.
- Levin, R. 1988. Statistik für Administratoren. 2 .. Auflage. Prentice Halle.
- Spiegel, M. 2009. Statistik. Schaum-Serie. 4 .. Auflage. Mcgraw Hügel.
- Walpole, R. 2007. Wahrscheinlichkeit und Statistik für Ingenieurwissenschaften und Naturwissenschaften. Pearson.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.