
Was ist der Unterschied zwischen Pfad und Verschiebung?
Das Hauptunterschied zwischen Flugbahn und Verschiebung ist, dass das letztere die Entfernung und Richtung ist, die ein Objekt zurücklegt, während das erstere der Weg oder die Form ist, die die Bewegung dieses Objekts annimmt.
Um jedoch die Unterschiede zwischen Verschiebung und Flugbahn deutlicher zu erkennen, ist es besser, die Konzeptualisierung anhand von Beispielen zu spezifizieren, die ein besseres Verständnis beider Begriffe ermöglichen..
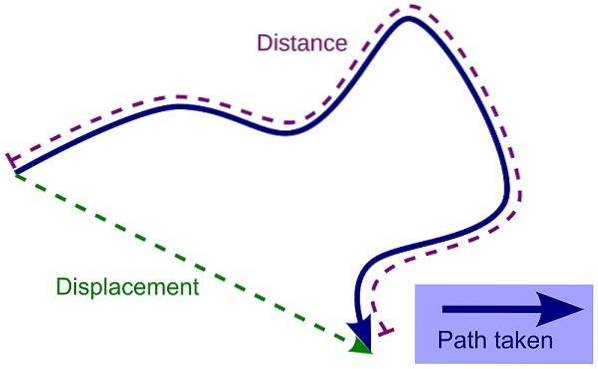
Verschiebung
Darunter versteht man die Entfernung und Richtung, die ein Objekt unter Berücksichtigung seiner Anfangsposition und seiner Endposition immer in einer geraden Linie zurücklegt. Für seine Berechnung werden, da es sich um eine Vektorgröße handelt, die als Zentimeter, Meter oder Kilometer bekannten Längenmaße verwendet..
Die Formel zur Berechnung der Verschiebung ist wie folgt definiert:
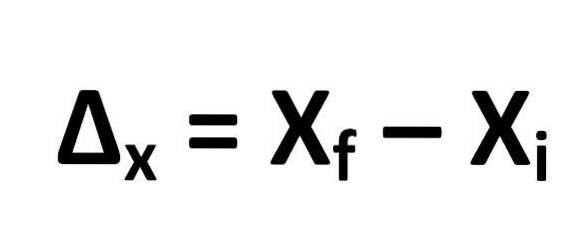
Daraus folgt:
- Δx = Verschiebung
- X.F. = Endposition des Objekts
- X.ich = Ausgangsposition des Objekts
Verschiebungsbeispiel
1- Wenn sich eine Gruppe von Kindern am Anfang einer Route befindet, deren Anfangsposition 50 m beträgt und sich in einer geraden Linie bewegt, bestimmen Sie die Verschiebung an jedem der Punkte X.F. .
- X.F. = 120 m
- X.F. = 90 m
- X.F. = 60 m
- X.F. = 40 m
2- Die Daten des Problems werden durch Ersetzen der Werte von X extrahiertzwei und X.1 in der Versatzformel:
- Δx = ?
- X.ich = 50 m
- Δx = X.F. - X.ich
- Δx = 120 m - 50 m = 70 m
3- In diesem ersten Ansatz sagen wir, dass Δx ist gleich 120m, was dem ersten Wert entspricht, den wir von X findenF., minus 50m, das ist der Wert von X.ich, Das Ergebnis sind 70 m, dh bei Erreichen von 120 m betrug die Verschiebung 70 m nach rechts.
4- Wir gehen auf die gleiche Weise vor, um die Werte von b, c und d zu lösen
- Δx = 90 m - 50 m = 40 m
- Δx = 60 m - 50 m = 10 m
- Δx = 40 m - 50 m = - 10 m
In diesem Fall ergab die Verschiebung ein negatives Ergebnis, dh die Endposition befindet sich in der entgegengesetzten Richtung zur Anfangsposition.
Flugbahn
Es ist die Route oder Linie, die von einem Objekt während seiner Bewegung und seiner Bewertung im internationalen System bestimmt wird und im Allgemeinen geometrische Formen wie Linie, Parabel, Kreis oder Ellipse annimmt. Es wird durch eine imaginäre Linie identifiziert und da es sich um eine skalare Größe handelt, wird es in Metern gemessen.
Es sollte beachtet werden, dass wir zur Berechnung der Flugbahn wissen müssen, ob sich der Körper in Ruhe oder in Bewegung befindet, dh dem von uns ausgewählten Referenzsystem unterworfen ist.
Die Gleichung zur Berechnung der Flugbahn eines Objekts im internationalen System lautet:
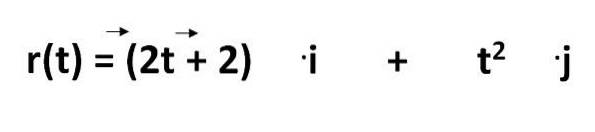
Davon müssen wir:
- r (t) = ist die Gleichung des Pfades
- 2t - 2 und tzwei = Koordinaten als Funktion der Zeit darstellen
- .Ich und .j = sind die Einheitsvektoren
Um die Berechnung des von einem Objekt zurückgelegten Pfades zu verstehen, werden wir das folgende Beispiel entwickeln:
- Berechnen Sie die Gleichung der Trajektorien der folgenden Positionsvektoren:
- r (t) = (2t + 7) .i + tzwei .j
- r (t) = (t - 2) .i + 2t .j
Erster Schritt: Da eine Pfadgleichung eine Funktion von X ist, definieren Sie dazu die Werte von X bzw. Y in jedem der vorgeschlagenen Vektoren:
1- Lösen Sie den ersten Positionsvektor:
- r (t) = (2t + 7) .i + tzwei .j
2- Ty = f (x), wobei X durch den Inhalt des Einheitsvektors gegeben ist .i und Y sind durch den Inhalt des Einheitsvektors gegeben .j:
- X = 2t + 7
- Y = tzwei
3- y = f (x), das heißt, Zeit ist nicht Teil des Ausdrucks, deshalb müssen wir ihn lösen, wir haben:
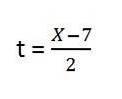
4- Wir ersetzen die Freigabe in Y. Es bleibt:
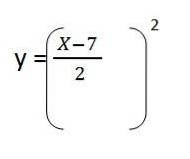
5- Wir lösen den Inhalt der Klammern und haben die Gleichung des resultierenden Pfades für den ersten Einheitsvektor:
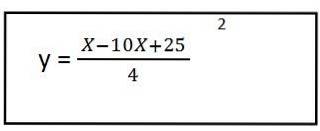
Wie wir sehen können, gab es eine Gleichung zweiten Grades, was bedeutet, dass die Flugbahn die Form einer Parabel hat.
Zweiter Schritt: Wir gehen auf die gleiche Weise vor, um die Trajektorie des zweiten Einheitsvektors zu berechnen
r (t) = (t - 2) .i + 2t .j
- X = t - 2
- Y = 2t
2- Nach den Schritten, die wir zuvor gesehen haben, y = f (x), müssen wir die Zeit löschen, da sie nicht Teil des Ausdrucks ist, bleibt uns Folgendes übrig:
- t = X + 2
3- Wir ersetzen die Freigabe in Y, verbleibende:
- y = 2 (X + 2)
4- Wenn wir die Klammern lösen, haben wir die Gleichung der resultierenden Trajektorie für den zweiten Einheitsvektor:
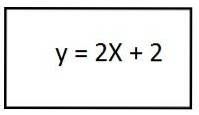
Bei diesem Verfahren war das Ergebnis eine gerade Linie, die uns sagt, dass die Flugbahn eine geradlinige Form hat.
Sobald die Konzepte von Verschiebung und Flugbahn verstanden sind, können wir den Rest der Unterschiede ableiten, die zwischen beiden Begriffen bestehen.
Weitere Unterschiede zwischen Verschiebung und Flugbahn
Verschiebung
- Dies ist die Entfernung und Richtung, die ein Objekt unter Berücksichtigung seiner Anfangsposition und seiner Endposition zurücklegt.
- Es passiert immer in einer geraden Linie.
- Es wird mit einem Pfeil erkannt.
- Verwenden Sie Längenmaße (Zentimeter, Meter, Kilometer)..
- Es ist eine Vektorgröße.
- Berücksichtigen Sie die zurückgelegte Richtung (rechts oder links)
- Die während der Tour verbrachte Zeit wird nicht berücksichtigt.
- Hängt nicht von einem Referenzsystem ab.
- Wenn der Startpunkt der gleiche Startpunkt ist, ist der Versatz Null.
- Das Modul muss mit dem zu fahrenden Raum übereinstimmen, solange der Pfad eine gerade Linie ist und sich die zu ändernde Richtung nicht ändert.
- Der Modul neigt dazu, zuzunehmen oder abzunehmen, wenn die Bewegung auftritt, wobei die Flugbahn berücksichtigt wird.
Flugbahn
Dies ist der Pfad oder die Linie, die ein Objekt während seiner Bewegung bestimmt. Nimmt geometrische Formen an (gerade, parabolisch, kreisförmig oder elliptisch).
- Es wird durch eine imaginäre Linie dargestellt.
- Es wird in Metern gemessen.
- Es ist eine skalare Größe.
- Die zurückgelegte Richtung wird nicht berücksichtigt.
- Berücksichtigen Sie die Zeit, die Sie während der Tour verbracht haben.
- Hängt von einem Referenzsystem ab.
- Wenn der Startpunkt oder die Anfangsposition mit der Endposition identisch ist, wird die Flugbahn durch die zurückgelegte Strecke angegeben.
- Der Wert der Trajektorie stimmt mit dem Modul des Verschiebungsvektors überein, wenn die resultierende Trajektorie eine gerade Linie ist, es jedoch keine Änderungen in der zu verfolgenden Richtung gibt.
- Erhöht sich immer, wenn sich der Körper bewegt, unabhängig von der Flugbahn.
Verweise
- Alvarado, N. (1972)) Physisch. Erstes Jahr der Wissenschaft. Editorial Fotoprin C.A. Venezuela.
- Fernández, M; Fidalgo, J. (2016). Physik und Chemie 1. Abitur. Editions Paraninfo, S.A. Spanien.
- Guatemaltekisches Institut für Radiopädagogik. (2011) Grundphysik. Zaculeu Group Erstes Semester. Guatemala.
- Fernández, P. (2014) Wissenschaftlich-technologischer Bereich. Paraninfo-Ausgaben. S.A. Spanien.
- Fisica Lab (2015) Vektorverschiebung. Wiederhergestellt von: fisicalab.com.
- Beispiele für. (2013) Verschiebung. Wiederhergestellt von: examplesde.com.
- Living Room Home Project (2014) Was ist Verschiebung? Wiederhergestellt von: salonhogar.net.
- Physiklabor (2015) Konzept der Flugbahn und Positionsgleichung. Wiederhergestellt von: fisicalab.com.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.