Das kartesische Koordinaten oder kartesisch sind solche, die durch orthogonale Projektion auf einen Punkt im dreidimensionalen Raum auf die drei kartesischen Achsen X, Y, Z erhalten werden.
Kartesische Achsen sind zueinander ausgerichtete Linien senkrecht zueinander. Im kartesischen Koordinatensystem werden jedem Punkt im Raum drei reelle Zahlen zugewiesen, die seine rechteckigen Koordinaten sind.
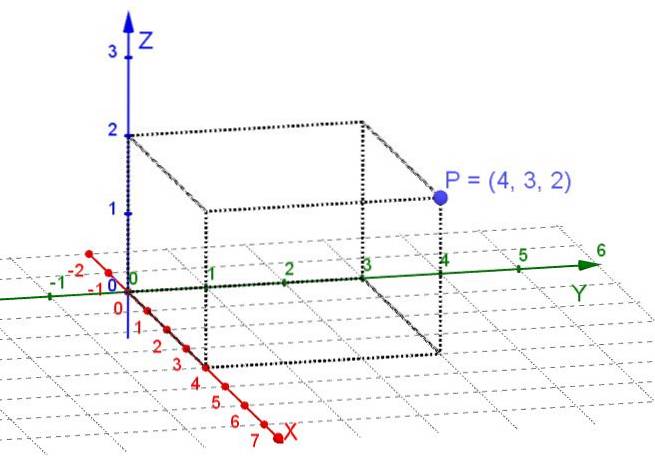
Eine Ebene ist ein Unterraum des dreidimensionalen Raums. Wenn Punkte in einer Ebene berücksichtigt werden, reicht es aus, ein Paar senkrechter Achsen X, Y als kartesisches System zu wählen. Dann werden jedem Punkt der Ebene zwei reelle Zahlen zugewiesen, die ihre rechteckigen Koordinaten sind.
Artikelverzeichnis
Rechteckige Koordinaten wurden ursprünglich vom französischen Mathematiker René Descartes (1596 und 1650) vorgeschlagen, weshalb sie als kartesisch bezeichnet werden.
Mit dieser Idee von Descartes werden den Punkten der Ebene und des Raums Zahlen zugewiesen, so dass den geometrischen Figuren eine algebraische Gleichung zugeordnet ist und die klassischen geometrischen Theoreme algebraisch bewiesen werden können. Mit kartesischen Koordinaten wird die analytische Geometrie geboren.
Wenn in einer Ebene zwei senkrechte Linien gewählt werden, die sich an einem Punkt O schneiden; und wenn zusätzlich jeder Linie eine Richtung und eine numerische Skala zwischen aufeinanderfolgenden äquidistanten Punkten zugewiesen wird, gibt es ein kartesisches System oder eine kartesische Ebene, in der jeder Punkt der Ebene einem geordneten Paar von zwei reellen Zahlen zugeordnet ist, die ihre Projektionen sind jeweils auf der X- und Y-Achse.
Die Punkte A = (3, 2); B = (- 2, 3); C = (- 2, -3) und D = (3, -3) sind in der kartesischen Ebene wie folgt dargestellt:
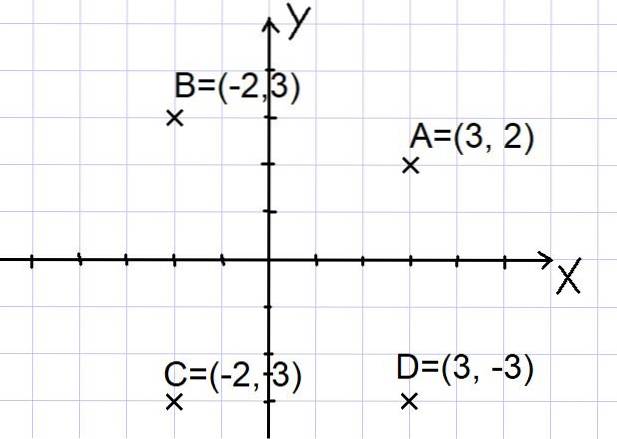
Beachten Sie, dass die beiden Achsen X und Y die Ebene in vier Sektoren unterteilen, die als Quadranten bezeichnet werden. Punkt A befindet sich im ersten Quadranten, B befindet sich im zweiten Quadranten, C befindet sich im dritten Quadranten und Punkt D befindet sich im vierten Quadranten..
Der Abstand zwischen zwei Punkten A und B auf der kartesischen Ebene ist die Länge des Segments, das sie verbindet. Dieser Abstand kann wie folgt analytisch berechnet werden:
d (A, B) = √ (Bx - Ax) ^ 2 + (By - Ay) ^ 2)
Die obige Formel wird durch Anwendung des Satzes von Pythagoras erhalten.
Wenn wir diese Formel auf die Punkte A, B in Abbildung 2 anwenden, haben wir:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
Das heißt, d (A, B) = 5,10 Einheiten. Beachten Sie, dass der Abstand ohne Messen mit einem Lineal ermittelt wurde. Es wurde ein vollständig algebraisches Verfahren angewendet.
Rechteckige Koordinaten ermöglichen die analytische Darstellung grundlegender geometrischer Objekte wie Punkt und Linie. Zwei Punkte A und B definieren eine einzelne Linie. Die Steigung der Linie ist definiert als der Quotient zwischen der Differenz der Y-Koordinaten von Punkt B minus A, geteilt durch die Differenz der X-Koordinaten von Punkt B minus A:
Steigung = (By - Ay) / (Bx - Axe)
Jeder Punkt P der Koordinaten (x, y), der zur Linie (AB) gehört, muss dieselbe Steigung haben:
Steigung = (y - Ay) / (x - Ax)
Die Gleichung, die durch die Gleichheit der Steigungen erhalten wird, ist die analytische oder algebraische Darstellung der Linie, die durch die Punkte A und B verläuft:
(y - Ay) / (x - Ax) = (By - Ay) / (Bx - Ax).
Wenn wir für A und B die rechteckigen Koordinaten von Abbildung 2 nehmen, haben wir:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
In diesem speziellen Fall haben wir eine Linie mit einer negativen Steigung -⅕, was bedeutet, dass durch Lokalisieren auf einem Punkt auf der Linie und Erhöhen der x-Koordinate um eine Einheit die y-Koordinate um 0,2 Einheiten abnimmt.
Die gebräuchlichste Methode, um die Gleichung der Linie in die Ebene zu schreiben, besteht darin, die y-Koordinate als Funktion der Variablen x zu löschen:
y = - (1/5) x + 13/5
Ermitteln Sie mit analytischen Methoden den Abstand zwischen den Punkten C und A als Rechteckkoordinaten von C = (-2, -3) und denen von A = (3,2)..
Die Formel für den euklidischen Abstand zwischen diesen beiden Punkten lautet wie folgt:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
Durch Ersetzen der entsprechenden rechteckigen Koordinaten haben wir:
d (A, C) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7,07
Erhalten Sie die Gleichung der Linie, die durch den Punkt C der Koordinaten (-2, -3) und den Punkt P der Koordinaten (2, 0) verläuft..
Zunächst wird die Steigung der Linie CP erhalten:
Steigung = (0 - (- 3)) / (2 - (-2)) = ¾
Jeder Punkt Q generischer Rechteckkoordinaten (x, y), der zur Linie CP gehört, muss dieselbe Steigung haben:
Steigung = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
Mit anderen Worten lautet die Gleichung der Linie CP:
(y +3) / (x +2) = ¾
Eine alternative Möglichkeit, die Gleichung der Linie CP zu schreiben, besteht darin, nach y zu lösen:
y = ¾ x - 3/2
Erhalten Sie die rechteckigen Koordinaten des Schnittpunkts zwischen den Linien y = - (1/5) x + 13/5 und der Linie y = ¾ x - 3/2.
Lösung: Per Definition haben die Schnittpunkte der beiden Linien dieselben rechteckigen Koordinaten. Daher sind die y-Koordinaten am Schnittpunkt für beide Linien identisch:
-(1/5) x + 13/5 = ¾ x - 3/2
was zu folgendem Ausdruck führt:
(¾ + ⅕) x = 13/5 +3/2
Lösen der Summe der Brüche, die wir erhalten:
19/20 x = 41/10
Auflösen nach x:
x = 82/19 = 4,32
Um den y-Achsenabschnitt zu erhalten, wird der erhaltene x-Wert in einer der folgenden Zeilen eingesetzt:
y = ¾ 4,32 - 3/2 = 1,74
Dies bedeutet, dass sich die gegebenen Linien am Punkt I der Koordinaten I = (4.32, 1.74) schneiden..
Erhalten Sie die Gleichung des Umfangs, der durch den Punkt R der Rechteckkoordinaten (3, 4) verläuft und dessen Mittelpunkt am Koordinatenursprung liegt.
Lösung: Der Radius R ist der Abstand vom Punkt R zum Ursprung O der Koordinaten (0, 0)..
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3 - 0) ^ 2 + (4 - 0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
Das heißt, es ist ein Kreis mit dem Radius 5, der bei (0,0) zentriert ist..
Jeder Punkt P (x, y) auf dem Umfang muss den gleichen Abstand 5 vom Zentrum (0, 0) haben, damit geschrieben werden kann:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
Nämlich:
√ (x ^ 2 + y ^ 2) = 5
Um die Quadratwurzel zu beseitigen, werden beide Mitglieder der Gleichheit quadriert und erhalten:
x ^ 2 + y ^ 2 = 25
Was ist die Gleichung des Umfangs.
Dieses Beispiel zeigt die Leistung des rechteckigen Koordinatensystems, mit dem geometrische Objekte wie der Umfang bestimmt werden können, ohne dass Papier, Bleistift und Kompass verwendet werden müssen. Der angeforderte Umfang wurde ausschließlich mit algebraischen Methoden bestimmt.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.