
Erhaltung des linearen Impulsprinzips, Beispiele, Übungen.
Das Erhaltung des linearen Impulses eines Körpers stellt fest, dass das Produkt seiner Masse und seines Geschwindigkeitsvektors eine konstante Größe ist, wenn der Körper frei von Wechselwirkungen mit anderen Körpern ist und die Geschwindigkeit in Bezug auf einen festen oder nicht beschleunigten Referenzrahmen gemessen wird.
Wenn Sie mehrere Körper haben, die nur miteinander, aber nicht mit der äußeren Umgebung interagieren, dann ist die linear Momentum des Satzes bleibt auch über die Zeit konstant.

Der lineare Impuls, der Impuls oder einfach der Schwung, wird durch den Buchstaben bezeichnet p y ist eine Vektorgröße:
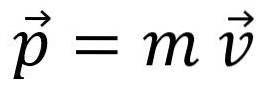
Das Momentum ist nicht dasselbe wie die Geschwindigkeit, obwohl die Beziehung offensichtlich ist: Zum Beispiel hat ein LKW mit 20 km / h mehr Momentum als ein Fahrrad, das sich mit der gleichen Geschwindigkeit bewegt.
Damit sich der lineare Impuls eines Körpers ändert, muss eine äußere Nettokraft auf ihn einwirken, sonst bleibt er konstant. Auch das lineare Moment P. eines Systems gebildet durch n-Körper ist die Vektorsumme der einzelnen Momente:
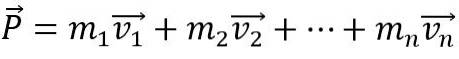
Artikelverzeichnis
- 1 Prinzip der Erhaltung des linearen Impulses
- 2 Beispiele
- 2.1 Beispiel 1
- 2.2 Beispiel 2
- 2.3 Beispiel 3
- 3 Anwendungen
- 3.1 Schiff im Weltraum
- 3.2 Alltag
- 4 Übungen
- 4.1 Übung 1
- 4.2 Übung 2
- 5 Referenzen
Prinzip der Erhaltung des linearen Impulses
In einem kraftfreien Körper (oder einem, in dem sich alle auf ihn einwirkenden Kräfte aufheben) kommt es vor, dass das lineare Moment konstant bleibt.
Das gleiche passiert in einem System, das aus mehreren Körpern besteht, die nur miteinander, aber nicht mit der äußeren Umgebung interagieren: Der gesamte lineare Impuls des Systems bleibt während der Entwicklung der Bewegung des Ganzen fest..
Dieses Erhaltungsprinzip wird wie folgt angegeben:
Der Gesamtimpuls einer Reihe von n-Körpern, die nur miteinander, nicht aber mit der äußeren Umgebung interagieren, ist eine unveränderliche zeitliche Größe.
Und mathematisch wird es wie folgt ausgedrückt:
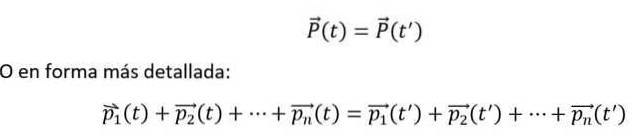
Die oben genannten Gleichheiten sind genau dann erfüllt, wenn die n-Körper interagieren miteinander, aber nicht mit der äußeren Umgebung. Darüber hinaus müssen einzelne Momente immer relativ zu einem Trägheitsreferenzrahmen gemessen werden..
Beispiele
Beispiel 1

Zwei Astronauten im Weltraum halten sich an den Händen und werden in einer festen Position relativ zum Raumschiff gehalten. Wenn sie sich jedoch gegenseitig drücken, beginnen sie sich vom Schiff aus gesehen in entgegengesetzte Richtungen zu trennen..
In diesem Fall ist der Gesamtimpuls nach dem Drücken immer noch der Anfangswert in Bezug auf das Raumfahrzeug, da die Interaktion zwischen den Astronauten nur durch die Kontaktkraft ihrer Hände zwischen ihnen erfolgt. Das heißt, Gesamtimpuls 0.
Der Schwung jedes Astronauten änderte sich jedoch. Anfänglich hatte jeder ein lineares Moment von 0 in Bezug auf das Schiff, aber nach dem Schieben tritt eines in eine Richtung und das andere in die entgegengesetzte Richtung aus, mit linearen Momenten ungleich Null gleicher Größe und entgegengesetzter Richtung..
Wenn also die einzelnen Momente vektoriell addiert werden, wird als Ergebnis der anfängliche Gesamtimpuls erhalten, der Null ist.
Andererseits zeigt die Erhaltung der Impulsgröße an, dass der Astronaut mit der niedrigsten Masse derjenige ist, der sich in Bezug auf das Raumschiff schneller bewegt. Das Ergebnis der Multiplikation seiner Masse mit seiner Geschwindigkeit ist jedoch gleich dem Produkt, das durch Multiplikation der Masse des anderen mit der Geschwindigkeit des anderen erhalten wird.
Beispiel 2
Ein Welpe ist auf einer schwimmenden Plattform in einem ruhigen See und sein Besitzer beobachtet ihn von einem Dock aus. Zu Beginn sind sowohl die Plattform als auch der Welpe in Ruhe, aber wenn der Welpe näher an den Besitzer heran möchte, bewegt sich die Plattform vom Dock weg.
Die Erklärung für diese Beobachtung liegt genau im Prinzip der Erhaltung der linearen Impulsmenge. Das System besteht aus dem Welpen und der Plattform.
Der Welpe kann dank der Reibungskraft zwischen seinen Beinen und der Oberfläche auf der Plattform laufen. In diesem Fall ist die Reibungskraft eine interne Wechselwirkungskraft zwischen ihm und der Plattform.
Das Ganze ist ein isoliertes System, da sich die Plattform ohne Bewegungswiderstand horizontal über den See bewegen kann. Andererseits werden in vertikaler Richtung alle Kräfte ausgeglichen und ausgeglichen, und das Ganze hat keine Bewegung in diese Richtung..
Daher sind in dieser Situation alle Hypothesen erfüllt, so dass das Prinzip der Erhaltung des linearen Impulses gilt.
Beispiel 3

Ein Eskimo ist in der Mitte eines zugefrorenen Sees gefangen, das Eis ist so glatt, dass der Eskimo, egal wie sehr er es versucht, ausrutscht und immer am selben Ort bleibt.
Der Eskimo kann nur dann aus dem See herauskommen, wenn er in die entgegengesetzte Richtung wirft, in die er einen schweren Gegenstand bewegen möchte, den er in seinem Rucksack trägt (vorausgesetzt, er trägt einen)..
Anwendungen
Schiff im Weltraum

Die Erhaltung des linearen Impulses wird angewendet, um eine Rakete in den Weltraum zu treiben, wo keine äußeren Kräfte vorhanden sind. In diesem Fall wird der Impuls des Schiffes durch Ausstoßen von Gasen mit hoher Geschwindigkeit erreicht, so dass sich die Rakete in die entgegengesetzte Richtung bewegen kann, in die sie ausgestoßen wurden..
Wenn das Schiff ursprünglich in Ruhe ist, wenn es Kraftstoff verbrennt und ausstößt, tritt die Ausstoßkraft gegen das Schiff selbst auf. Es ist eine innere Kraft zwischen den Gasen und dem Schiff. Es gibt keine äußeren Kräfte und daher gilt die Erhaltung des linearen Impulses.
Da der lineare Impuls der Gase der gleiche und dem des Schiffes entgegengesetzt ist, gelingt es ihm, aus der Ruhe zu kommen, und indem er weiterhin Gase ausstößt, erhöht er seine Bewegungsmenge und damit seine Geschwindigkeit.
Alltag

Ein weiterer Fall der Anwendung der Erhaltung des linearen Impulses im Alltag besteht darin, einen Nagel in das Holz zu schlagen und dabei die Bewegung oder den Impuls des Hammers auszunutzen..
Es könnte argumentiert werden, dass in diesem Fall das Prinzip nicht gilt, weil es eine äußere Kraft gibt: den Widerstand, den das Holz dem Nagel bietet..
Im Moment des Kontakts ist die Kraft, die der Hammer auf den Nagel ausübt, jedoch eine innere Kraft (zwischen dem System, das der Nagel ist, und dem Hammer), die viel größer ist als der Widerstand, dem das Holz entgegenwirkt, und daher ist letzterer vernachlässigbar.
Der gesamte Impuls des Hammers, der aufgrund seiner großen Masse und Geschwindigkeit ziemlich groß ist, wird unmittelbar nach der Kollision auf den Nagel übertragen. Beachten Sie, dass der gesamte Moment, aber nicht die gesamte kinetische Energie des Hammers übertragen wird, da ein Teil davon im Nagel und im Hammer in Wärmeenergie umgewandelt wird, die ihre Temperatur nach dem Aufprall erhöht.
Ausbildung
Übung 1
Die Astronauten Andrew und Berenice befinden sich außerhalb der Raumstation und halten beide Hände und ruhen relativ zur Station. Sie werden angetrieben, indem die Hände eines gegen das andere gedrückt werden, und sie werden freigegeben. Wenn Andrew, 70 kg Masse, sich mit 1 m / s in Bezug auf die Station bewegt, wie schnell ist Berenice mit 49 kg Masse??
Lösung
In diesem Fall gelten eindeutig die Hypothesen zur Erhaltung des linearen Impulses, da im Weltraum keine äußeren Kräfte vorhanden sind. Die Kraft, mit der beide Astronauten ihre Hände drücken, ist eine innere Kraft.
Angenommen, Andrews Masse ist M.zu und das von Berenice M.b. Ebenso sind die Geschwindigkeiten von beiden nach dem Impuls V.zu für Andrew und V.b für Berenice. Dann gilt die Erhaltung des linearen Impulses wie folgt:
M.zu∙0 + M.b∙0 = M.zu∙V.zu+ M.b∙V.b
Wenn wir nach Berenices Geschwindigkeit suchen, haben wir:
V.b = - (M.zu / M.b) ∙ V.zu
Platzieren der numerischen Werte:
V.b = - (70/49) ∙ (1 m / s) oder = -1,43 m / s oder
Das heißt, Berenice bewegt sich mit einer Geschwindigkeit von 1,43 m / s in die entgegengesetzte Richtung zu der von Andrew.
Übung 2

Ein Welpe mit einer Masse von 5 kg ruht auf einer 15 kg schweren Plattform, die ebenfalls in Ruhe auf einem stillen See schwimmt. Wenn der Welpe mit einer Geschwindigkeit von 0,5 m / s auf der Plattform zu laufen beginnt. Wie schnell werden der Welpe und die Plattform in Bezug auf einen am Boden befestigten Beobachter sein??
Lösung
Das Trägheitsreferenzsystem wird als Dock verwendet, an dem sich der Besitzer des Welpen befindet. Zunächst ruhen sowohl der Welpe als auch die schwimmende Plattform in Bezug auf das Dock..
Wenn der Welpe beschließt, schnell auf den Besitzer zuzugehen v ' relativ zur Plattform bewegt sich die Plattform dann mit Geschwindigkeit vom Pier weg +V.. Die Geschwindigkeit des Welpen in Bezug auf die Feder wird mittels der Vektorsumme seiner Geschwindigkeit in Bezug auf die Plattform plus der Geschwindigkeit der Plattform erhalten und wir bezeichnen sie mit:
v = -v' + V.
Da der Widerstand des Wassers gegen die Bewegung der Plattform aufgrund seiner geringen Geschwindigkeit praktisch gleich Null ist, kann festgestellt werden, dass das System aus besteht der Welpe + die Plattform ist ein isoliertes System und es gilt das Prinzip der Erhaltung des linearen Impulses:
0 = m ≤ v + M ≤ V.
Denken Sie daran, dass v = v '+ V wir haben:
0 = -m ≤ v '+ m ≤ v + M ≤ V.
Das heißt: m ∙ v '= (m + M) ∙ V.
Daher ist V = [m / (m + M)] v 'und v = - (M / m) V = - [M / (m + M)] v'
Ersetzen Sie die numerischen Werte, die wir haben:
V = [5 / (5 + 15)] ≤ 0,5 m / s = 0,125 m / s
Dies ist die Geschwindigkeit, mit der sich die Plattform vom Dock entfernt.
V = - (15/20) ≤ 0,5 m / s = -0,375 m / s
Und das ist die Geschwindigkeit, mit der sich der Welpe dem Dock nähert.
Verweise
- Duke University. Partikelsysteme. Wiederhergestellt von: webhome.phy.duke.edu.
- Rex, A. 2011. Grundlagen der Physik. Pearson.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1. Pearson.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.
- .


Welcome to the world of adult Dating loveawake.ru