
Unelastische Abstürze in einer Dimension und Beispiele
Das unelastische Schocks oder unelastische Kollisionen sind eine kurze und intensive Wechselwirkung zwischen zwei Objekten, bei denen der Impuls erhalten bleibt, nicht jedoch die kinetische Energie, von der ein Prozentsatz in eine andere Art von Energie umgewandelt wird.
Abstürze oder Kollisionen sind in der Natur häufig. Subatomare Partikel kollidieren mit extrem hohen Geschwindigkeiten, während viele Sportarten und Spiele aus kontinuierlichen Kollisionen bestehen. Sogar Galaxien können kollidieren.

In der Realität bleibt der Impuls bei jeder Art von Kollision erhalten, solange die kollidierenden Partikel ein isoliertes System bilden. In diesem Sinne gibt es also kein Problem. Jetzt haben Objekte kinetische Energie, die mit der Bewegung verbunden ist, die sie haben. Was kann mit dieser Energie passieren, wenn sie kollidiert??
Die inneren Kräfte, die während der Kollision zwischen Objekten auftreten, sind stark. Wenn festgestellt wird, dass kinetische Energie nicht erhalten bleibt, bedeutet dies, dass sie in andere Energiearten umgewandelt wird: zum Beispiel in Schallenergie (eine spektakuläre Kollision hat einen charakteristischen Klang)..
Weitere Verwendungsmöglichkeiten für kinetische Energie: Reibungswärme und natürlich die unvermeidliche Verformung, die Objekte bei Kollisionen erfahren, wie z. B. die Karosserien der Autos in der obigen Abbildung.
Artikelverzeichnis
- 1 Beispiele für unelastische Kollisionen
- 2 Perfekt unelastische Kollisionen in einer Dimension
- 3 Rückerstattungskoeffizient
- 4 Ermittlung des Rückerstattungskoeffizienten?
- 5 Arbeitsbeispiele
- 5.1 -Übung 1
- 5.2 -Übung 2
- 5.3 -Übung 3
- 6 Referenzen
Beispiele für unelastische Kollisionen
- Zwei Plastilinmassen kollidieren und kleben zusammen und bewegen sich nach der Kollision als ein Stück.
- Ein Gummiball, der von einer Wand oder einem Boden abprallt. Der Ball verformt sich, wenn er auf die Oberfläche trifft.
Mit wenigen Ausnahmen wird nicht die gesamte kinetische Energie in andere Energiearten umgewandelt. Objekte können eine bestimmte Menge dieser Energie behalten. Später werden wir sehen, wie der Prozentsatz berechnet wird.
Wenn die kollidierenden Teile zusammenkleben, wird die Kollision als vollkommen unelastisch bezeichnet, und beide neigen dazu, sich zusammen zu bewegen..
Perfekt unelastische Kollisionen in einer Dimension
Die Kollision in der Abbildung zeigt zwei Objekte unterschiedlicher Masse m1 Y. mzwei, sich mit Geschwindigkeit aufeinander zu bewegen vi1 Y. vi2 beziehungsweise. Alles geschieht in der Horizontalen, das heißt, es ist eine Kollision in einer Dimension, die am einfachsten zu untersuchen ist.
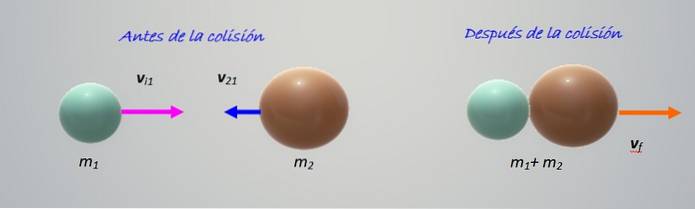
Die Objekte kollidieren und haften dann zusammen, indem sie sich nach rechts bewegen. Es ist eine vollkommen unelastische Kollision, also müssen wir nur den Schwung behalten:
P.oder = P.F.
Der Impuls ist ein Vektor, dessen SI-Einheiten Ns sind. In der beschriebenen Situation kann auf die Vektornotation verzichtet werden, wenn Kollisionen in einer Dimension behandelt werden:
mvoder = mvF.
Der Impuls des Systems ist die Vektorsumme des Impulses jedes Teilchens.
m1 vi1 + mzwei vi2 = (m1 + mzwei) vF.
Die Endgeschwindigkeit ist gegeben durch:
vF. = (m1 vi1 + mzwei vi2) / (m1 + mzwei)
Restitutionskoeffizient
Es gibt eine Größe, die angeben kann, wie elastisch eine Kollision ist. Es geht um Rückerstattungskoeffizient, Dies ist definiert als der negative Quotient zwischen der Relativgeschwindigkeit der Partikel nach der Kollision und der Relativgeschwindigkeit vor der Kollision.
Lass dich1 und duzwei die jeweiligen Geschwindigkeiten der Partikel zunächst. Und sei v1 und V.zwei die jeweiligen Endgeschwindigkeiten. Mathematisch kann der Restitutionskoeffizient wie folgt ausgedrückt werden:
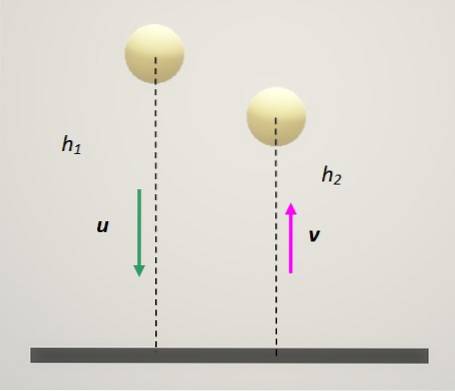
- Wenn ε = 0 ist, entspricht dies der Bestätigung, dass vzwei = v1. Dies bedeutet, dass die Endgeschwindigkeiten gleich sind und die Kollision unelastisch ist, wie im vorherigen Abschnitt beschrieben..
- Wenn ε = 1 ist, bedeutet dies, dass sich die relativen Geschwindigkeiten sowohl vor als auch nach der Kollision nicht ändern. In diesem Fall ist die Kollision elastisch.
- Und wenn 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.
Wie man den Restitutionskoeffizienten bestimmt?
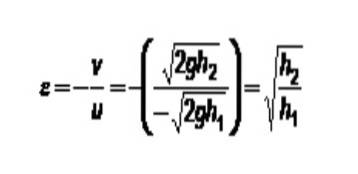
Der Restitutionskoeffizient hängt von der Klasse der an der Kollision beteiligten Materialien ab. Ein sehr interessanter Test, um festzustellen, wie elastisch ein Material ist, um Kugeln herzustellen, besteht darin, die Kugel auf eine feste Oberfläche fallen zu lassen und die Rückprallhöhe zu messen.

In diesem Fall hat die feste Platte immer die Geschwindigkeit 0. Wenn ihr Index 1 zugewiesen ist und der Kugelindex 2 lautet:



Zu Beginn wurde vorgeschlagen, dass die gesamte kinetische Energie in andere Energiearten umgewandelt werden kann. Energie wird schließlich nicht zerstört. Ist es möglich, dass sich bewegende Objekte kollidieren und zu einem einzigen Objekt vereinigen, das plötzlich zur Ruhe kommt? Das ist nicht so leicht vorstellbar.
Stellen wir uns jedoch vor, es passiert umgekehrt, wie in einem umgekehrten Film. Das Objekt befand sich also zunächst in Ruhe und explodierte dann in verschiedene Teile. Diese Situation ist durchaus möglich: Es ist eine Explosion.
Eine Explosion kann also als eine vollkommen unelastische Kollision angesehen werden, die in der Zeit zurück betrachtet wird. Die Dynamik bleibt ebenfalls erhalten, und es kann festgestellt werden, dass:
P.oder = P.F.
Arbeitsbeispiele
-Übung 1
Aus Messungen ist bekannt, dass der Restitutionskoeffizient von Stahl 0,90 beträgt. Eine Stahlkugel wird aus einer Höhe von 7 m auf eine feste Platte fallen gelassen. Berechnung:
a) Wie hoch wird es springen?.
b) Wie lange dauert es zwischen dem ersten Kontakt mit der Oberfläche und dem zweiten.
Lösung
a) Die Gleichung, die zuvor im Abschnitt zur Bestimmung des Restitutionskoeffizienten abgeleitet wurde, wird verwendet:
Die Höhe wird gelöscht hzwei::
0,90zwei . 7 m = 5,67 m
b) Damit es 5,67 Meter ansteigt, ist eine Geschwindigkeit erforderlich, die gegeben ist durch:


t max = voder/ g = (10,54 / 9,8 s) = 1,08 s.
Die Zeit für die Rückkehr ist dieselbe, daher beträgt die Gesamtzeit für die Besteigung der 5,67 Meter und die Rückkehr zum Startpunkt die doppelte maximale Zeit:
tFlug = 2,15 s.
-Übung 2
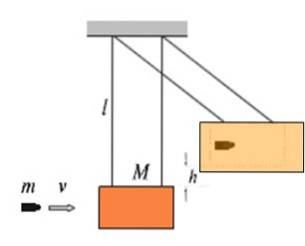
Die Figur zeigt einen Holzblock der Masse M, der in Ruhe an Schnüren der Länge l wie ein Pendel hängt. Dies wird als ballistisches Pendel bezeichnet und dient zur Messung der Eintrittsgeschwindigkeit v in eine Kugel der Masse m. Je höher die Geschwindigkeit ist, mit der die Kugel auf den Block trifft, desto höher steigt sie.
Die Kugel im Bild ist in den Block eingebettet, daher handelt es sich um einen völlig unelastischen Schock.

Angenommen, eine 9,72-g-Kugel trifft auf den 4,60 kg schweren Massenblock, dann steigt die Baugruppe um 16,8 cm aus dem Gleichgewicht. Was ist die Geschwindigkeit v von der Kugel?
Lösung
Während der Kollision bleibt der Impuls erhalten und oderF. ist die Geschwindigkeit des Ganzen, sobald sich die Kugel in den Block eingebettet hat:
P.oder = P.F.
Der Block befindet sich zunächst in Ruhe, während die Kugel mit Geschwindigkeit auf das Ziel gerichtet ist v::
m.v + M.0 = (m + M) uF.
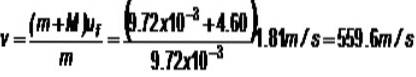
Nicht bekannt oderF. noch, aber nach der Kollision bleibt die mechanische Energie erhalten, wobei dies die Summe der potentiellen Gravitationsenergie U und der kinetischen Energie K ist:
Anfängliche mechanische Energie = Endgültige mechanische Energie
UNDmo = E.mf
ODERoder + K.oder = U.F. + K.F.
Die potentielle Energie der Gravitation hängt von der Höhe ab, bis zu der der Satz reicht. Für die Gleichgewichtsposition ist die Anfangshöhe diejenige, die als Referenzniveau genommen wird, daher:
ODERoder = 0
Dank der Kugel hat das Ganze kinetische Energie K.oder, Dies wird in potentielle Gravitationsenergie umgewandelt, wenn der Satz seine maximale Höhe erreicht h. Die kinetische Energie ist gegeben durch:
K = ½ mvzwei
Anfangs ist die kinetische Energie:
K.oder = (1/2) (M + m) uF.zwei
Denken Sie daran, dass die Kugel und der Block bereits ein einziges Massenobjekt bilden M + m. Die potentielle Energie der Gravitation, wenn sie ihre maximale Höhe erreicht haben, ist:
ODERF. = (m + M) gh
Deshalb:
K.oder = U.F.
(1/2) (M + m) uF.zwei = (m + M) gh
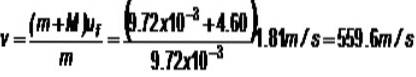
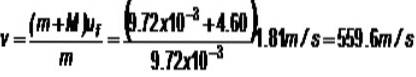
-Übung 3
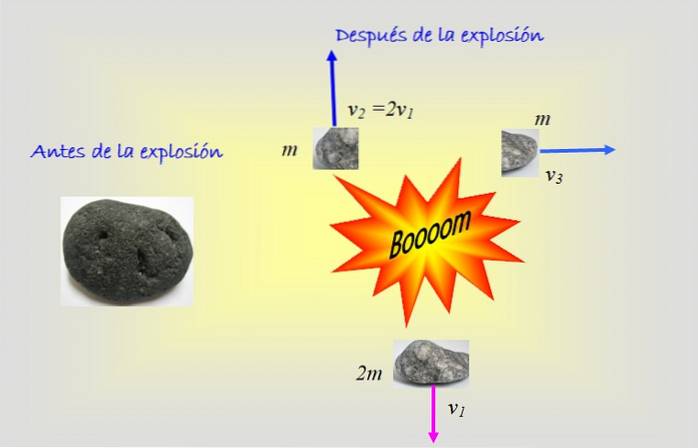
Das Objekt in der Figur explodiert in drei Fragmente: zwei mit gleicher Masse m und ein größeres mit einer Masse von 2 m. Die Abbildung zeigt die Geschwindigkeiten jedes Fragments nach der Explosion. Was war die Anfangsgeschwindigkeit des Objekts??
Lösung
In diesem Problem müssen zwei Koordinaten verwendet werden: x und Y., weil zwei der Fragmente vertikale Geschwindigkeiten haben, während der Rest horizontale Geschwindigkeit hat.
Die Gesamtmasse des Objekts ist die Summe der Masse aller Fragmente:
M = m + m + 2 m = 4 m
Der Impuls bleibt sowohl in der x-Achse als auch in der y-Achse erhalten, es wird separat angegeben:
- 4m. oderx= m v3
- 4m. oderY. = m. 2v1 - 2m. v1
Beachten Sie, dass sich das große Fragment mit der Geschwindigkeit v1 nach unten bewegt, um anzuzeigen, dass ein negatives Vorzeichen darauf gesetzt wurde.
Aus der zweiten Gleichung folgt sofort das oderY. = 0, und vom ersten wird ux sofort gelöscht:

Verweise
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6th. Ed Prentice Hall. 175-181
- Rex, A. 2011. Grundlagen der Physik. Pearson. 135-155.
- Serway, R., Vulle, C. 2011. Grundlagen der Physik. 9n / A Lernen einbinden. 172-182
- Tipler, P. (2006) Physik für Wissenschaft und Technologie. 5. Aufl. Band 1. Editorial Reverté. 217-238
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. MacGraw Hill. 185-195



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.