
Schwerpunkt Eigenschaften, Berechnung, Beispiele
Das Schwerpunkt eines Körpers messbarer Größe ist der Punkt, an dem sein Gewicht als angewendet gilt. Es ist daher eines der Grundkonzepte der Statik.
Der erste Ansatz bei den Problemen der Elementarphysik besteht in der Annahme, dass sich jedes Objekt wie eine Punktmasse verhält, dh keine Dimensionen hat und die gesamte Masse in einem einzigen Punkt konzentriert ist. Dies gilt für eine Box, ein Auto, einen Planeten oder ein subatomares Teilchen. Dieses Modell ist bekannt als Teilchenmodell.

Dies ist natürlich eine Annäherung, die für viele Anwendungen sehr gut funktioniert. Es ist keine leichte Aufgabe, das individuelle Verhalten von Tausenden und Millionen von Partikeln zu berücksichtigen, die jedes Objekt enthalten kann.
Die realen Dimensionen der Dinge müssen jedoch berücksichtigt werden, wenn Ergebnisse erzielt werden sollen, die näher an der Realität liegen. Da wir uns im Allgemeinen in der Nähe der Erde befinden, ist die allgegenwärtige Kraft auf jeden Körper genau das Gewicht.
Artikelverzeichnis
- 1 Überlegungen zur Ermittlung des Schwerpunkts
- 2 Wie berechnet sich der Schwerpunkt??
- 3 Eigenschaften
- 3.1 -Finden des Schwerpunkts eines Körpers im statischen Gleichgewicht
- 3.2 - Gelöstes Beispiel
- 4 Unterschied zum Schwerpunkt
- 5 Beispiele für den Schwerpunkt
- 5.1 Schwerpunkt unregelmäßiger Gegenstände
- 5.2 Objekte ausgleichen
- 6 Referenzen
Überlegungen zur Ermittlung des Schwerpunkts
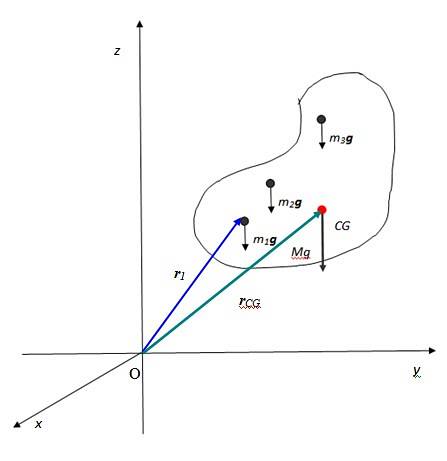
Wenn die Körpergröße berücksichtigt werden soll, wo genau soll Gewicht angewendet werden? Wenn Sie ein beliebig kontinuierliches Objekt haben, ist sein Gewicht a verteilte Kraft zwischen jedem seiner Bestandteile.
Lassen Sie diese Teilchen m sein1, mzwei, m3… Jeder von ihnen erfährt seine entsprechende Gravitationskraft m1g, mzweig, m3g…, alle parallel. Dies ist so, da das Gravitationsfeld der Erde in den allermeisten Fällen als konstant angesehen wird, da die Objekte im Vergleich zur Größe des Planeten klein und nahe an seiner Oberfläche sind..
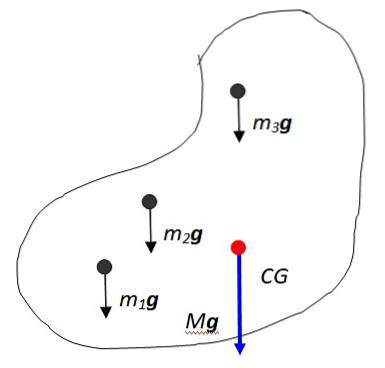
Die Vektorsumme dieser Kräfte ergibt das Gewicht des Objekts, das auf den Punkt angewendet wird, der als Schwerpunkt bezeichnet wird und in der Figur als CG bezeichnet wird und dann mit dem übereinstimmt Massenzentrum. Der Schwerpunkt ist wiederum der Punkt, an dem die gesamte Masse als konzentriert betrachtet werden kann.
Das resultierende Gewicht hat Größe Mg wo M. ist die Gesamtmasse des Objekts und ist natürlich vertikal auf den Erdmittelpunkt gerichtet. Die Summationsnotation ist nützlich, um die Gesamtmasse des Körpers auszudrücken:
Der Schwerpunkt fällt nicht immer mit einem Materialpunkt zusammen. Zum Beispiel befindet sich der Schwerpunkt eines Rings in seinem geometrischen Zentrum, wo es selbst keine Masse gibt. Wenn Sie jedoch die auf einen Reifen einwirkenden Kräfte analysieren möchten, müssen Sie das Gewicht genau auf diesen Punkt anwenden.
In den Fällen, in denen das Objekt eine beliebige Form hat, kann sein Massenschwerpunkt, wenn es homogen ist, immer noch berechnet werden, indem das gefunden wird Schwerpunkt oder Schwerpunkt der Figur.
Wie berechnet man den Schwerpunkt??
Wenn der Schwerpunkt (CG) und der Schwerpunkt (cm) zusammenfallen, wenn das Gravitationsfeld gleichmäßig ist, kann im Prinzip der cm berechnet und das Gewicht darauf aufgebracht werden.
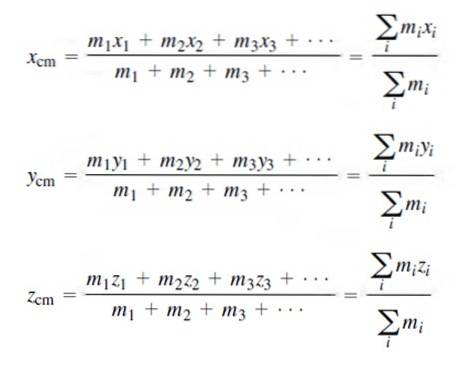
Betrachten wir zwei Fälle: Der erste ist einer, in dem die Massenverteilung diskret ist; Das heißt, jede Masse, aus der das System besteht, kann gezählt und mit einer Zahl i versehen werden, wie dies im vorherigen Beispiel getan wurde.
Die Koordinaten des Massenschwerpunkts für eine diskrete Massenverteilung sind:
Natürlich entspricht die Summe aller Massen der Gesamtmasse des Systems M, wie oben angegeben..
Die drei Gleichungen werden unter Berücksichtigung des Vektors r auf eine kompakte Form reduziertcm oder Positionsvektor des Massenschwerpunkts:
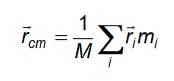
Und im Fall einer kontinuierlichen Massenverteilung, bei der die Partikel eine unterschiedliche Größe haben und nicht unterschieden werden können, um sie zu zählen, wird die Summe durch ein Integral ersetzt, das über das Volumen des betreffenden Objekts gebildet wird:
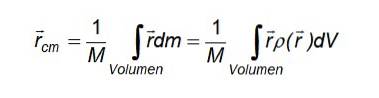
Wo r ist der Positionsvektor einer Differenzmasse dm und die Definition der Massendichte wurde verwendet, um das Massendifferential auszudrücken dm in einem Volumendifferential enthalten dV::
Eigenschaften
Einige wichtige Überlegungen zum Massenschwerpunkt sind:
- Obwohl ein Referenzsystem erforderlich ist, um die Positionen zu bestimmen, hängt der Schwerpunkt nicht von der Wahl des Systems ab, da er eine Eigenschaft des Objekts ist.
- Wenn das Objekt eine Achse oder eine Symmetrieebene hat, liegt der Schwerpunkt auf dieser Achse oder Ebene. Das Ausnutzen dieses Umstands spart Rechenzeit.
- Alle auf das Objekt einwirkenden äußeren Kräfte können auf den Schwerpunkt ausgeübt werden. Das Verfolgen der Bewegung dieses Punktes gibt eine globale Vorstellung von der Bewegung des Objekts und erleichtert die Untersuchung seines Verhaltens..
-Finden des Schwerpunkts eines Körpers im statischen Gleichgewicht
Angenommen, Sie möchten, dass sich der Körper in der vorherigen Abbildung im statischen Gleichgewicht befindet, dh er wird nicht um eine beliebige Rotationsachse verschoben oder gedreht, die O sein kann.

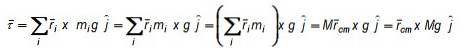
-Gearbeitetes Beispiel
Ein dünner Stab aus einheitlichem Material ist 6 m lang und wiegt 30 N. Am linken Ende wird ein Gewicht von 50 N und am rechten Ende ein Gewicht von 20 N aufgehängt. Finden Sie: a) die Größe der Aufwärtskraft, die erforderlich ist, um das Gleichgewicht der Stange aufrechtzuerhalten, b) den Schwerpunkt des Satzes.
Lösung
Das Kraftdiagramm ist in der folgenden Abbildung dargestellt. Das Gewicht der Stange wird an ihrem Schwerpunkt aufgebracht, der mit ihrem geometrischen Mittelpunkt übereinstimmt. Die einzige berücksichtigte Abmessung des Balkens ist seine Länge, da die Aussage angibt, dass er dünn ist.
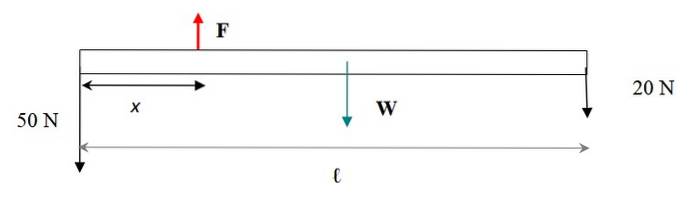
Damit das Balken + Gewichte-System im Translationsgleichgewicht bleibt, muss die Summe der Kräfte Null sein. Die Kräfte sind vertikal, wenn wir mit Vorzeichen + nach oben und mit Vorzeichen nach unten betrachten - dann:
F - 50 - 20 - 30 N = 0
F = 100 N.
Diese Kraft garantiert das translatorische Gleichgewicht. Nehmen Sie die Torsionsmomente aller Kräfte in Bezug auf eine Achse, die durch das linke Ende des Systems verläuft, und wenden Sie die Definition an:
t = r x F.
Die Momente all dieser Kräfte um den ausgewählten Punkt sind senkrecht zur Ebene des Balkens:
tF. = xF = 100x
tW. = - (1/2) mg = -3 m. 30 N = -90 Nm
t1 = 0 (da die 50 N Kraft durch die ausgewählte Drehachse geht und kein Moment ausübt)
tzwei = -lFzwei = 6 m. 20 N = -120 Nm
Deshalb:
100 x -90-120 Nm = 0
x = 2,10 m
Der Schwerpunkt der Stange + eingestellte Gewichte befindet sich 2,10 Meter vom linken Ende der Stange entfernt.
Unterschied zum Schwerpunkt
Der Schwerpunkt fällt wie angegeben mit dem Schwerpunkt zusammen, solange das Gravitationsfeld der Erde für alle zu berücksichtigenden Punkte des Objekts konstant ist. Das Gravitationsfeld der Erde ist nichts anderes als der bekannte und bekannte Wert von g = 9,8 m / szwei senkrecht nach unten gerichtet.
Obwohl der Wert von g mit dem Breitengrad und der Höhe variiert, wirken sich diese normalerweise nicht auf die Objekte aus, die sich die meiste Zeit befinden. Es wäre ganz anders, wenn Sie einen großen Körper in der Nähe der Erde betrachten, zum Beispiel einen Asteroiden, der sehr nahe am Planeten ist.
Der Asteroid hat einen eigenen Schwerpunkt, aber sein Schwerpunkt müsste seitdem nicht mehr damit übereinstimmen G Angesichts der Größe des Asteroiden und der Tatsache, dass die Gewichte der einzelnen Partikel möglicherweise nicht parallel sind, würden wahrscheinlich erhebliche Größenunterschiede auftreten.
Ein weiterer grundlegender Unterschied besteht darin, dass der Schwerpunkt unabhängig davon gefunden wird, ob auf das Objekt eine Kraft namens Gewicht ausgeübt wird oder nicht. Es ist eine intrinsische Eigenschaft des Objekts, die uns zeigt, wie seine Masse in Bezug auf seine Geometrie verteilt ist.
Der Schwerpunkt liegt unabhängig davon, ob Gewicht aufgebracht wird oder nicht. Und es befindet sich an derselben Position, auch wenn sich das Objekt auf einen anderen Planeten bewegt, auf dem das Gravitationsfeld unterschiedlich ist..
Andererseits ist der Schwerpunkt eindeutig mit der Gewichtsanwendung verbunden, wie wir in den vorhergehenden Absätzen gesehen haben..
Beispiele für den Schwerpunkt
Schwerpunkt unregelmäßiger Gegenstände
Es ist sehr leicht herauszufinden, wo sich der Schwerpunkt eines unregelmäßigen Objekts wie einer Tasse befindet. Zunächst wird es an einem beliebigen Punkt aufgehängt und von dort aus eine vertikale Linie gezeichnet (in Abbildung 5 ist es die Fuchsia-Linie im linken Bild)..
Es wird dann an einem anderen Punkt aufgehängt und eine neue Vertikale gezeichnet (türkisfarbene Linie im rechten Bild). Der Schnittpunkt beider Linien ist der Schwerpunkt des Bechers.

Objekte ausbalancieren
Lassen Sie uns die Stabilität eines auf der Straße fahrenden Lastwagens analysieren. Wenn der Schwerpunkt über der Basis des Flurförderzeugs liegt, kippt das Flurförderzeug nicht um. Das Bild links ist die stabilste Position.
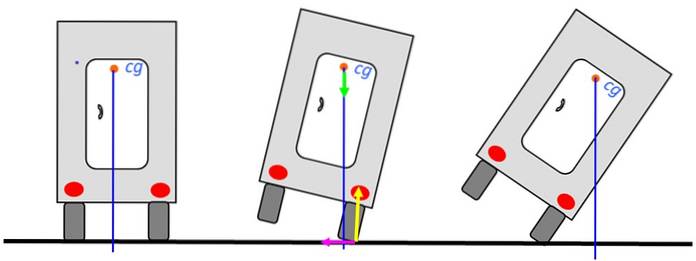
Selbst wenn der Stapler nach rechts geneigt ist, kann er wie in der mittleren Zeichnung in eine stabile Gleichgewichtsposition zurückkehren, da die Vertikale immer noch durch die Basis verläuft. Wenn diese Linie jedoch außerhalb des Lastwagens verläuft, kippt sie um.
Das Diagramm zeigt die Kräfte am Drehpunkt: normal in gelb, Gewicht in grün und statische Reibung links in Fuchsia. Normal und Reibung werden auf die Drehachse aufgebracht, so dass sie kein Drehmoment ausüben. Daher tragen sie nicht zum Umkippen des Lastwagens bei.
Das Gewicht bleibt, das zum Glück gegen den Uhrzeigersinn ein Drehmoment ausübt und dazu neigt, das Flurförderzeug in seine Gleichgewichtsposition zurückzubringen. Beachten Sie, dass die vertikale Linie durch die Auflagefläche verläuft, bei der es sich um den Reifen handelt.
Wenn sich das Fahrzeug ganz rechts befindet, ändert sich das Drehmoment des Gewichts im Uhrzeigersinn. Wenn der LKW ein anderes Mal nicht kontert werden kann, kippt er um.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill. 247-253.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6.… Ed Prentice Hall. 229-238.
- Resnick, R. (1999). Körperlich. Vol. 1. 3rd Ed. In Spanisch. Compañía Editorial Continental S.A. de C.V. 331-341.
- Rex, A. 2011. Grundlagen der Physik. Pearson, 146-155.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Volume 1.340-346.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.