Das Axiome von Wahrscheinlichkeit es sind mathematische Sätze, die sich auf die Wahrscheinlichkeitstheorie beziehen und keinen Beweis verdienen. Die Axiome wurden 1933 vom russischen Mathematiker Andrei Kolmogorov (1903-1987) in seiner Arbeit aufgestellt Grundlagen der Wahrscheinlichkeitstheorie und legte den Grundstein für die mathematische Untersuchung der Wahrscheinlichkeit.
Bei der Durchführung eines bestimmten zufälligen Experiments ξ ist der Probenraum E die Menge aller möglichen Ergebnisse des Experiments, auch genannt Veranstaltungen. Jedes Ereignis wird als A bezeichnet und P (A) ist die Wahrscheinlichkeit seines Auftretens. Dann stellte Kolmogorov fest, dass:
-Axiom 1 (nicht Negativität): Die Wahrscheinlichkeit, dass ein Ereignis A auftritt, ist immer positiv oder Null, P (A) ≥ 0. Wenn die Wahrscheinlichkeit eines Ereignisses 0 ist, wird es aufgerufen unmögliches Ereignis.
-Axiom 2 (Gewissheit): Wenn ein Ereignis zu E gehört, beträgt seine Eintrittswahrscheinlichkeit 1, was wir als ausdrücken können P (E) = 1. Es ist das, was als bekannt ist sicheres Ereignis, denn bei der Durchführung eines Experiments gibt es mit Sicherheit ein Ergebnis.
-Axiom 3 (Zusatz): bei zwei oder mehr inkompatiblen Ereignissen zwei mal zwei, genannt A.1, ZUzwei, ZU3…, Die Wahrscheinlichkeit, dass Ereignis A eintritt1 plus die A.zwei plus die A.3 und so weiter, es ist die Summe der Wahrscheinlichkeiten, die jeder einzeln auftritt.
Dies wird ausgedrückt als: P (A.1 U A.zwei U A.3 U…) = P (A.1) + P (A.zwei) + P (A.3) + ...
Artikelverzeichnis
Die Axiome der Wahrscheinlichkeit werden in einer Vielzahl von Anwendungen häufig verwendet. Beispielsweise:
Ein Reißnagel oder eine Wende wird in die Luft geworfen, und wenn er auf den Boden fällt, besteht die Möglichkeit, mit dem Punkt nach oben (U) oder mit dem Punkt nach unten (D) zu landen (andere Möglichkeiten werden nicht berücksichtigt). Der Probenraum dieses Experiments besteht aus diesen Ereignissen, dann ist E = U, D.
Durch Anwendung der Axiome haben wir:
P (E) = 1 (Axiom 2)
Aber P (E) = P (U) + P (D) (Axiom 3), weil diese Ereignisse nicht miteinander kompatibel oder unzusammenhängend sind. Der Reißnagel fällt nicht gleichzeitig mit der Spitze nach oben oder unten, sondern ist der eine oder andere, aber nicht beide, da andere Möglichkeiten nicht in Betracht gezogen werden. Dann:
P (U) + P (D) = 1
P (U) = 1 - P (D)
Ob es gleich wahrscheinlich ist, nach oben oder unten zu landen, P (U) = P (D) = ½ (Axiom 1). Es kann jedoch sein, dass die Konstruktion und das Design des Reißzwecks eher in die eine oder andere Richtung fallen. Zum Beispiel kann es sein, dass P (U) = ¾ während P (D) = ¼ (Axiom 1).
Beachten Sie, dass in beiden Fällen die Summe der Wahrscheinlichkeiten 1 ergibt. Die Axiome geben jedoch nicht an, wie die Wahrscheinlichkeiten zuzuweisen sind, zumindest nicht vollständig. Aber sie bestätigen, dass sie Zahlen zwischen 0 und 1 sind und dass, wie in diesem Fall, die Summe aller 1 ist.
Die Wahrscheinlichkeitsaxiome sind keine Methode zur Zuordnung des Wahrscheinlichkeitswerts. Hierfür gibt es drei Optionen, die mit den Axiomen kompatibel sind:
Jedem Ereignis wird die gleiche Eintrittswahrscheinlichkeit zugewiesen, dann ist die Eintrittswahrscheinlichkeit wie folgt definiert:
P (A) = Anzahl der für Ereignis A günstigen Fälle / Anzahl möglicher Fälle
Wie hoch ist beispielsweise die Wahrscheinlichkeit, ein Ass aus einem Kartenspiel mit französischen Karten zu ziehen? Das Deck hat 52 Karten, 13 von jeder Farbe und es gibt 4 Farben. Jeder Anzug hat 1 Asse, also gibt es insgesamt 4 Asse:
P (as) = 4/52 = 1/13
Die Laplace-Regel ist auf endliche Stichprobenräume beschränkt, in denen jedes Ereignis gleich wahrscheinlich ist.
Hier muss das Experiment wiederholbar sein, da die Methode auf der Durchführung einer großen Anzahl von Wiederholungen basiert..
Lassen Sie uns i Wiederholungen des Experiments ξ machen, von denen wir feststellen, dass n die Häufigkeit ist, mit der ein bestimmtes Ereignis A auftritt. Dann ist die Wahrscheinlichkeit, dass dieses Ereignis auftritt, wie folgt:
P (A) = limi → ∞ (weder)
Wobei n / i die relative Häufigkeit eines Ereignisses ist.
Die Definition von P (A) auf diese Weise erfüllt Kolmogorovs Axiome, hat jedoch den Nachteil, dass viele Tests durchgeführt werden müssen, damit die Wahrscheinlichkeit angemessen ist.
Eine Person oder eine Gruppe von Personen kann vereinbaren, die Wahrscheinlichkeit einem Ereignis nach eigenem Ermessen zuzuweisen. Diese Methode hat den Nachteil, dass unterschiedliche Personen demselben Ereignis unterschiedliche Wahrscheinlichkeiten zuweisen können..
Erhalten Sie im Experiment des gleichzeitigen Werfens von 3 ehrlichen Münzen die Wahrscheinlichkeiten der beschriebenen Ereignisse:
a) 2 Köpfe und ein Schwanz.
b) 1 Kopf und zwei Schwänze
c) 3 Kreuze.
d) Mindestens 1 Gesicht.
Köpfe werden mit C und Schwänze mit X bezeichnet. Es gibt jedoch verschiedene Möglichkeiten, zwei Köpfe und einen Schwanz zu erhalten. Zum Beispiel können die ersten beiden Münzen Köpfe und die dritte Schwänze landen. Oder der erste kann Köpfe fallen, der zweite Schwanz und der dritte Kopf. Und schließlich können die ersten Schwänze und die restlichen Köpfe sein.
Um die Fragen zu beantworten, müssen alle Möglichkeiten bekannt sein, die in einem Tool namens beschrieben werden Baum diagramm oder Baum der Wahrscheinlichkeiten::
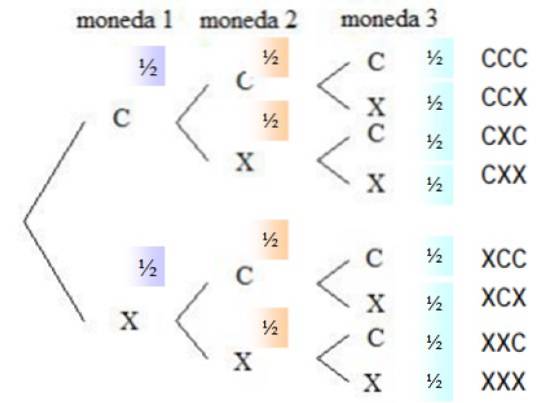
Die Wahrscheinlichkeit, dass eine Münze mit dem Kopf herauskommt, beträgt ½, das Gleiche gilt für den Schwanz, da die Münze ehrlich ist. In der rechten Spalte sind alle Möglichkeiten aufgelistet, die der Wurf hat, dh der Probenraum.
Aus dem Probenraum werden die Kombinationen ausgewählt, die auf das angeforderte Ereignis reagieren, da die Reihenfolge, in der die Gesichter angezeigt werden, nicht wichtig ist. Es gibt drei günstige Ereignisse: CCX, CXC und XCC. Die Wahrscheinlichkeit, dass jedes Ereignis eintritt, ist:
P (CCX) = ½. ½. ½ = 1/8
Das Gleiche gilt für die CXC- und XCC-Ereignisse. Jedes Ereignis hat eine Wahrscheinlichkeit von 1/8. Daher ist die Wahrscheinlichkeit, genau 2 Köpfe zu bekommen, die Summe der Wahrscheinlichkeiten aller günstigen Ereignisse:
P (2-seitig) = 1/8 + 1/8 + 1/8 = 3/8 = 0,375
Das Ermitteln der Wahrscheinlichkeit, dass genau zwei Kreuze auftreten, ist ein Problem analog zum vorherigen. Es gibt auch drei günstige Ereignisse aus dem Probenraum: CXX, XCX und XXC. Deshalb:
P (2 Kreuze) = 3/8 = 0,375
Intuitiv wissen wir, dass die Wahrscheinlichkeit, 3 Schwänze (oder 3 Köpfe) zu bekommen, geringer ist. In diesem Fall ist das gesuchte Ereignis XXX am Ende der rechten Spalte, dessen Wahrscheinlichkeit ist:
P (XXX) = ½. ½. ½ = 1/8 = 0,125.
Es wird verlangt, mindestens 1 Gesicht zu erhalten. Dies bedeutet, dass 3 Gesichter, 2 Gesichter oder 1 Gesicht herauskommen können. Das einzige Ereignis, das damit nicht kompatibel ist, ist das, bei dem 3 Schwänze herauskommen, deren Wahrscheinlichkeit 0,125 beträgt. Daher ist die gesuchte Wahrscheinlichkeit:
P (mindestens 1 Kopf) = 1 - 0,125 = 0,875.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.