
Historischer Hintergrund der analytischen Geometrie

Das Historischer Hintergrund der analytischen Geometrie Sie stammen aus dem 17. Jahrhundert, als Pierre de Fermat und René Descartes ihre Grundidee definierten. Seine Erfindung folgte der Modernisierung der Algebra und der algebraischen Notation von François Viète..
Dieses Gebiet hat seine Stützpunkte im antiken Griechenland, insbesondere in den Werken von Apollonius und Euklid, die auf diesem Gebiet der Mathematik einen großen Einfluss hatten..
Die wesentliche Idee hinter der analytischen Geometrie ist, dass eine Beziehung zwischen zwei Variablen, so dass eine eine Funktion der anderen ist, eine Kurve definiert. Diese Idee wurde zuerst von Pierre de Fermat entwickelt. Dank dieses wesentlichen Rahmens konnten Isaac Newton und Gottfried Leibniz den Kalkül entwickeln.
Der französische Philosoph Descartes entdeckte auch eine algebraische Herangehensweise an die Geometrie, anscheinend allein. Descartes 'Arbeit zur Geometrie erscheint in seinem berühmten Buch Diskurs der Methode.
Dieses Buch weist darauf hin, dass der Kompass und die geradlinigen geometrischen Konstruktionen Addition, Subtraktion, Multiplikation und Quadratwurzeln beinhalten..
Die analytische Geometrie repräsentiert die Vereinigung zweier wichtiger Traditionen in der Mathematik: Geometrie als Studium der Form sowie Arithmetik und Algebra, die mit Quantität oder Zahlen zu tun haben. Analytische Geometrie ist daher die Untersuchung des Feldes der Geometrie unter Verwendung von Koordinatensystemen.
Geschichte
Hintergrund der analytischen Geometrie
Die Beziehung zwischen Geometrie und Algebra hat sich im Laufe der Geschichte der Mathematik weiterentwickelt, obwohl die Geometrie einen früheren Reifegrad erreicht hat.
Zum Beispiel konnte der griechische Mathematiker Euklid in seinem klassischen Buch viele Ergebnisse organisieren Die Elemente.
Aber es war der antike griechische Apollonius von Perga, der in seinem Buch die Entwicklung der analytischen Geometrie vorhersagte Kegel. Er definierte einen Kegel als Schnittpunkt zwischen einem Kegel und einer Ebene.
Unter Verwendung von Euklids Ergebnissen an ähnlichen Dreiecken und Sekanten von Kreisen fand er eine Beziehung, die durch die Abstände von einem beliebigen Punkt "P" eines Kegels zu zwei senkrechten Linien, der Hauptachse eines Kegels und der Tangente an einem Endpunkt der Achse gegeben ist . Apollonius nutzte diese Beziehung, um grundlegende Eigenschaften der Kegel abzuleiten.
Die spätere Entwicklung von Koordinatensystemen in der Mathematik erfolgte erst, nachdem die Algebra dank islamischer und indischer Mathematiker gereift war..
Bis zur Renaissance wurde Geometrie verwendet, um Lösungen für algebraische Probleme zu rechtfertigen, aber es gab nicht viel, was Algebra zur Geometrie beitragen konnte..
Diese Situation würde sich mit der Annahme einer geeigneten Notation für algebraische Beziehungen und der Entwicklung des jetzt möglichen Konzepts einer mathematischen Funktion ändern.
Jahrhundert XVI
Ende des 16. Jahrhunderts führte der französische Mathematiker François Viète die erste systematische algebraische Notation ein, bei der Buchstaben zur Darstellung bekannter und unbekannter numerischer Größen verwendet wurden..
Er entwickelte auch leistungsfähige allgemeine Methoden zum Arbeiten algebraischer Ausdrücke und zum Lösen algebraischer Gleichungen..
Dank dessen waren Mathematiker nicht vollständig auf geometrische Figuren und geometrische Intuition angewiesen, um Probleme zu lösen..
Sogar einige Mathematiker begannen, die geometrische Standard-Denkweise aufzugeben, nach der lineare Variablen von Längen und Quadraten Flächen entsprechen, während kubische Variablen Volumen entsprechen..
Die ersten, die diesen Schritt unternahmen, waren der Philosoph und Mathematiker René Descartes sowie der Anwalt und Mathematiker Pierre de Fermat..
Grundlage der analytischen Geometrie
Descartes und Fermat gründeten in den 1630er Jahren unabhängig voneinander die analytische Geometrie und übernahmen die Algebra von Viète für die Untersuchung des Ortes.
Diese Mathematiker erkannten, dass Algebra ein mächtiges Werkzeug in der Geometrie ist und erfanden das, was heute als analytische Geometrie bekannt ist..
Ein Durchbruch, den sie erzielten, bestand darin, Viète zu schlagen, indem Buchstaben verwendet wurden, um Entfernungen darzustellen, die variabel und nicht fest sind..
Descartes verwendete Gleichungen, um geometrisch definierte Kurven zu untersuchen, und betonte die Notwendigkeit, allgemeine algebraisch-grafische Kurven von Polynomgleichungen in Grad "x" und "y" zu berücksichtigen..
Fermat seinerseits betonte, dass jede Beziehung zwischen den Koordinaten "x" und "y" eine Kurve bestimmt.
Mit diesen Ideen restrukturierte er Apollonius 'Aussagen zu algebraischen Begriffen und stellte einige seiner verlorenen Arbeiten wieder her..
Fermat gab an, dass jede quadratische Gleichung in "x" und "y" in der Standardform eines der konischen Abschnitte platziert werden kann. Trotzdem hat Fermat seine Arbeiten zu diesem Thema nie veröffentlicht.
Dank ihrer Fortschritte konnte Archimedes nur sehr schwer lösen, und in Einzelfällen konnten Fermat und Descartes schnell und für eine große Anzahl von Kurven (heute als algebraische Kurven bekannt) lösen..
Seine Ideen fanden jedoch erst durch die Bemühungen anderer Mathematiker in der zweiten Hälfte des 17. Jahrhunderts allgemeine Akzeptanz..
Die Mathematiker Frans van Schooten, Florimond de Beaune und Johan de Witt halfen bei der Erweiterung von Decartes 'Arbeiten und fügten wichtiges zusätzliches Material hinzu..
Beeinflussen
In England hat John Wallis die analytische Geometrie populär gemacht. Er verwendete Gleichungen, um die Kegel zu definieren und ihre Eigenschaften abzuleiten. Obwohl er negative Koordinaten frei verwendete, war es Isaac Newton, der zwei schräge Achsen verwendete, um die Ebene in vier Quadranten zu unterteilen.
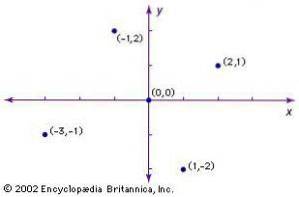
Newton und der deutsche Gottfried Leibniz revolutionierten Ende des 17. Jahrhunderts die Mathematik, indem sie die Kraft der Analysis unabhängig demonstrierten..
Newton demonstrierte die Bedeutung analytischer Methoden für die Geometrie und ihre Rolle in der Analysis, als er behauptete, dass jeder Würfel (oder jede algebraische Kurve dritten Grades) drei oder vier Standardgleichungen für geeignete Koordinatenachsen hat. Mit Hilfe von Newton selbst bewies der schottische Mathematiker John Stirling dies 1717.
Analytische Geometrie von drei und mehr Dimensionen
Obwohl sowohl Descartes als auch Fermat vorschlugen, drei Koordinaten zur Untersuchung von Kurven und Oberflächen im Raum zu verwenden, entwickelte sich die dreidimensionale analytische Geometrie bis 1730 langsam..
Die Mathematiker Euler, Hermann und Clairaut erstellten allgemeine Gleichungen für Zylinder, Kegel und Rotationsflächen..
Zum Beispiel verwendete Euler Gleichungen für Übersetzungen im Raum, um die allgemeine quadratische Oberfläche so zu transformieren, dass ihre Hauptachsen mit ihren Koordinatenachsen übereinstimmen.
Euler, Joseph-Louis Lagrange und Gaspard Monge machten die analytische Geometrie unabhängig von der synthetischen (nicht analytischen) Geometrie.
Verweise
- Die Entwicklung der analytischen Geometrie (2001). Von encyclopedia.com wiederhergestellt
- Geschichte der analytischen Geometrie (2015). Von maa.org wiederhergestellt
- Analyse (Mathematik). Von britannica.com wiederhergestellt
- Analytische Geometrie. Von britannica.com wiederhergestellt
- Descartes und die Geburt der analytischen Geometrie. Von sciencedirect.com wiederhergestellt


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.