Das relative Geschwindigkeit eines Objekts ist eines, das in Bezug auf einen bestimmten Beobachter gemessen wird, da ein anderer Beobachter eine andere Messung erhalten kann. Die Geschwindigkeit hängt immer vom Beobachter ab, der sie misst.
Daher ist die Geschwindigkeit eines Objekts, die von einer bestimmten Person gemessen wird, die relative Geschwindigkeit in Bezug auf dieses Objekt. Ein anderer Beobachter kann einen anderen Wert für die Geschwindigkeit erhalten, selbst wenn es sich um dasselbe Objekt handelt.
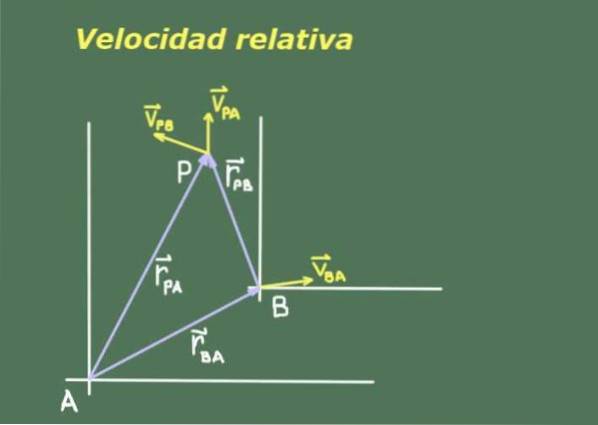
Da zwei Beobachter A und B, die sich relativ zueinander bewegen, unterschiedliche Messungen eines dritten sich bewegenden Objekts P haben können, ist es notwendig, nach einer Beziehung zwischen den Positionen und Geschwindigkeiten von P zu suchen, die von A und B gesehen werden.
Abbildung 1 zeigt zwei Beobachter A und B mit ihren jeweiligen Bezugssystemen, von denen aus sie die Position und Geschwindigkeit des Objekts P messen.
Jeder Beobachter A und B misst die Position und Geschwindigkeit des Objekts P zu einem bestimmten Zeitpunkt t. In der klassischen (oder galiläischen) Relativitätstheorie ist die Zeit für Beobachter A unabhängig von ihrer relativen Geschwindigkeit dieselbe wie für Beobachter B..
In diesem Artikel geht es um die klassische Relativitätstheorie, die für die meisten alltäglichen Situationen gültig und anwendbar ist, in denen Objekte eine Geschwindigkeit haben, die viel langsamer ist als die des Lichts..
Wir bezeichnen die Position des Beobachters B in Bezug auf A als rBA. Da die Position eine Vektorgröße ist, verwenden wir Fettdruck, um sie anzuzeigen. Die Position des Objekts P in Bezug auf A wird als bezeichnet rPA und das des gleichen Objekts P in Bezug auf B. rPB.
Artikelverzeichnis
Zwischen diesen drei Positionen besteht eine Vektorbeziehung, die aus der Darstellung in Abbildung 1 abgeleitet werden kann:
rPA= rPB + rBA
Wenn die Ableitung des vorherigen Ausdrucks in Bezug auf die Zeit genommen wird t Wir werden die Beziehung zwischen den relativen Geschwindigkeiten jedes Beobachters erhalten:
V.PA= V.PB + V.BA
Im vorherigen Ausdruck haben wir die relative Geschwindigkeit von P in Bezug auf A als Funktion der relativen Geschwindigkeit von P in Bezug auf B und die relative Geschwindigkeit von B in Bezug auf A..
In ähnlicher Weise kann die Relativgeschwindigkeit von P in Bezug auf B als Funktion der Relativgeschwindigkeit von P in Bezug auf A und der Relativgeschwindigkeit von A in Bezug auf B geschrieben werden.
V.PB= V.PA + V.AB
Es ist anzumerken, dass die Relativgeschwindigkeit von A in Bezug auf B gleich und entgegengesetzt zu der von B in Bezug auf A ist:
V.AB = -V.BA
Ein Auto fährt auf einer geraden Straße, die von West nach Ost führt, mit einer Geschwindigkeit von 80 km / h, während in der entgegengesetzten Richtung (und von der anderen Spur) ein Motorrad mit einer Geschwindigkeit von 100 km / h fährt.
Ein Junge fährt auf dem Rücksitz des Autos und möchte die relative Geschwindigkeit eines Motorrads wissen, das sich ihm nähert. Um die Antwort herauszufinden, wendet das Kind die Beziehungen an, die es gerade im vorherigen Abschnitt gelesen hat, und identifiziert jedes Koordinatensystem wie folgt:
-A ist das Koordinatensystem eines Beobachters auf der Straße, und in Bezug darauf wurden die Geschwindigkeiten jedes Fahrzeugs gemessen.
-B ist das Auto und P ist das Motorrad.
Wenn Sie die Geschwindigkeit von Motorrad P in Bezug auf Auto B berechnen möchten, wird die folgende Beziehung angewendet:
V.PB= V.PA + V.AB=V.PA - V.BA
Wenn wir die West-Ost-Richtung als positiv betrachten, haben wir:
V.PB= (-100 km / h - 80 km / h) ich = -180 km / h ich
Dieses Ergebnis wird wie folgt interpretiert: Das Motorrad bewegt sich relativ zum Auto mit einer Geschwindigkeit von 180 km / h und Richtung -ich, das heißt, von Ost nach West.
Das Motorrad und das Auto haben sich auf ihrer Fahrspur gekreuzt. Das Kind auf dem Rücksitz des Autos sieht, wie sich das Motorrad wegbewegt, und möchte nun wissen, wie schnell es sich von ihm wegbewegt, vorausgesetzt, dass sowohl das Motorrad als auch das Auto die gleiche Geschwindigkeit wie vor dem Überqueren beibehalten..
Um die Antwort zu erfahren, wendet das Kind dieselbe Beziehung an, die zuvor verwendet wurde:
V.PB= V.PA + V.AB=V. PA - V.BA
V.PB= -100 km / h ich - 80 km / h ich = -180 km / h ich
Und jetzt bewegt sich das Motorrad mit der gleichen Relativgeschwindigkeit vom Auto weg, mit der es sich näherte, bevor sie überquerten..
Das gleiche Motorrad aus Teil 2 wird mit der gleichen Geschwindigkeit von 100 km / h zurückgegeben, ändert jedoch seine Richtung. Das heißt, das Auto (das mit einer Geschwindigkeit von 80 km / h weiterfährt) und das Motorrad bewegen sich beide in eine positive Ost-West-Richtung..
Ab einem bestimmten Punkt fährt das Motorrad am Auto vorbei, und das Kind auf dem Rücksitz des Autos möchte die relative Geschwindigkeit des Motorrads in Bezug auf ihn wissen, wenn es es vorbeifahren sieht..
Um die Antwort zu erhalten, wendet das Kind die Relativbewegungsverhältnisse erneut an:
V.PB= V.PA + V.AB=V.PA - V.BA
V.PB= +100 km / h ich - 80 km / h ich = 20 km / h ich
Das Kind vom Rücksitz aus beobachtet, wie das Motorrad das Auto mit einer Geschwindigkeit von 20 km / h überholt.
Ein Motorboot überquert einen 600 m breiten Fluss, der von Norden nach Süden fließt. Die Geschwindigkeit des Flusses beträgt 3 m / s. Die Geschwindigkeit des Bootes in Bezug auf das Wasser des Flusses beträgt 4 m / s nach Osten.
(i) Finden Sie die Geschwindigkeit des Bootes relativ zum Flussufer.
(ii) Geben Sie die Geschwindigkeit und Richtung des Bootes relativ zum Land an.
(iii) Berechnen Sie die Übergangszeit.
(iv) Wie weit wird es sich vom Startpunkt nach Süden bewegt haben?.
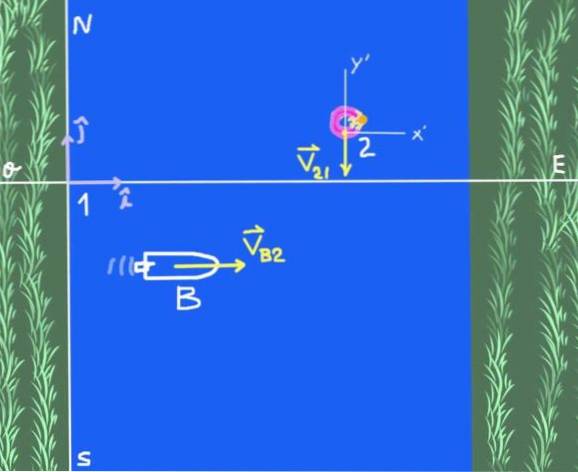
Es gibt zwei Referenzsysteme: das Solidarreferenzsystem am Flussufer, das wir 1 nennen werden, und das Referenzsystem 2, bei dem es sich um einen Beobachter handelt, der auf dem Flusswasser schwimmt. Gegenstand der Studie ist Boot B..
Die Geschwindigkeit des Bootes relativ zum Fluss wird in Vektorform wie folgt geschrieben:
V.B2 = 4 ich Frau
Die Geschwindigkeit von Beobachter 2 (Floß auf dem Fluss) in Bezug auf Beobachter 1 (an Land):
V.einundzwanzig = -3 j Frau
Sie möchten die Geschwindigkeit des Bootes in Bezug auf Land finden V.B1.
V.B1 = V.B2 + V.einundzwanzig
V.B1 = (4 ich - 3 j) Frau
Die Geschwindigkeit des Bootes ist der Modul der vorherigen Geschwindigkeit:
|V.B1| = (42 + (-3) 2) ½ = 5 m / s
Und die Adresse lautet:
θ = Arctan (-¾) = -36,87º
Die Überquerungszeit des Bootes ist der Quotient zwischen der Breite des Flusses und der x-Komponente der Geschwindigkeit des Bootes in Bezug auf Land.
t = (600 m) / (4 m / s) = 150 s
Um die Drift zu berechnen, die das Boot nach Süden hatte, wird die y-Komponente der Geschwindigkeit des Bootes in Bezug auf Land mit der Überquerungszeit multipliziert:
d = -3 j m / s * 150 s = -450 j m
Die Verschiebung nach Süden gegenüber dem Startpunkt beträgt 450 m.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.