
Vektoren im Raum, wie man grafisch darstellt, Anwendungen, Übungen
EIN Vektor im Raum wird jeder durch ein Koordinatensystem dargestellt, das durch gegeben ist x, Y. Y. z. Fast immer das Flugzeug xy ist die Ebene der horizontalen Fläche und der Achse z steht für Höhe (oder Tiefe).
Die in Abbildung 1 gezeigten kartesischen Koordinatenachsen unterteilen den Raum in 8 Regionen, die als bezeichnet werden Oktanten, analog zu wie Achsen x - Y. Teilen Sie die Ebene in 4 Quadranten. Wir werden dann 1. Oktant, 2. Oktant und so weiter haben.
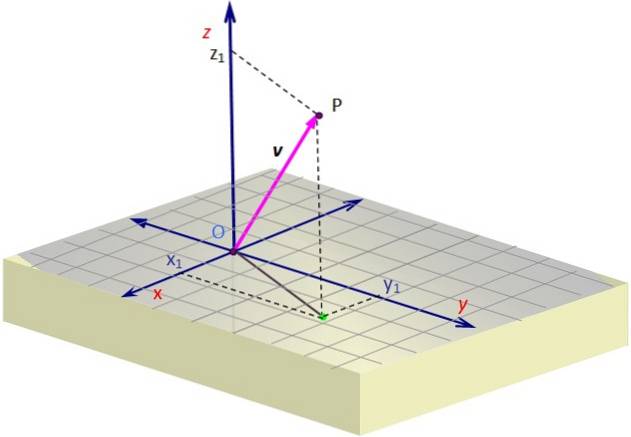
1 enthält eine Darstellung eines Vektors v Im Weltall. Eine gewisse Perspektive ist erforderlich, um die Illusion von drei Dimensionen in der Ebene des Bildschirms zu erzeugen, was durch Zeichnen einer Schrägansicht erreicht wird.
Verwenden Sie zum Zeichnen eines 3D-Vektors die gepunkteten Linien, die die Koordinaten der Projektion oder des "Schattens" von auf dem Raster bestimmen v Über die Oberfläche x-y. Diese Projektion beginnt bei O und endet am grünen Punkt.
Dort müssen Sie entlang der Vertikalen bis zur erforderlichen Höhe (oder Tiefe) entsprechend dem Wert von fortfahren z, bis zum Erreichen von P. Der Vektor wird ausgehend von O gezeichnet und endet bei P, das im Beispiel im 1. Oktanten liegt.
Artikelverzeichnis
- 1 Anwendungen
- 2 Notation und Darstellung von Vektoren in 3D
- 2.1 Winkel und Regiekosinus eines Vektors
- 3 Gelöste Übungen
- 3.1 -Übung 1
- 3.2 -Übung 2
- 4 Referenzen
Anwendungen
Vektoren im Raum werden häufig in der Mechanik und anderen Bereichen der Physik und Technik verwendet, da die uns umgebenden Strukturen eine dreidimensionale Geometrie erfordern..
Positionsvektoren im Raum werden verwendet, um Objekte relativ zu einem aufgerufenen Referenzpunkt zu positionieren Quelle O. Daher sind sie auch notwendige Werkzeuge in der Navigation, aber das ist noch nicht alles.
Kräfte, die auf Strukturen wie Bolzen, Klammern, Kabel, Streben und mehr wirken, sind von Natur aus vektoriell und räumlich orientiert. Um seine Wirkung zu kennen, ist es notwendig, seine Adresse (und auch seinen Anwendungsort) zu kennen..
Und häufig ist die Richtung einer Kraft bekannt, indem man zwei Punkte im Raum kennt, die zu ihrer Wirkungslinie gehören. Auf diese Weise ist die Kraft:
F. = F. oder
Wobei F die Größe oder der Modul der Kraft ist und oder ist der Einheitsvektor (des Moduls 1), der entlang der Wirkungslinie von gerichtet ist F..
Notation und 3D-Vektordarstellungen
Bevor wir mit der Lösung einiger Beispiele fortfahren, werden wir kurz die 3D-Vektornotation überprüfen.
In dem Beispiel in 1 hat der Vektor v, dessen Ursprungspunkt mit dem Ursprung O übereinstimmt und dessen Ende der Punkt P ist, Koordinaten x Y. z positiv, während die Koordinate Y. ist negativ. Diese Koordinaten sind: x1, Y.1, z1, das sind genau die Koordinaten von P..
Wenn wir also einen Vektor haben, der mit dem Ursprung verknüpft ist, dh dessen Startpunkt mit O übereinstimmt, ist es sehr einfach, seine Koordinaten anzugeben, die die des Extrempunkts oder P sind. Um zwischen einem Punkt und einem Vektor zu unterscheiden, Wir werden bis zu den letzten fetten Buchstaben und Klammern wie folgt verwenden:
v = < x1, Y.1, z1 >
Während Punkt P in Klammern angegeben ist:
P = (x1, Y.1, z1)
Eine andere Darstellung verwendet Einheitsvektoren ich, j Y. k das definiert die drei Raumrichtungen auf den Achsen x, Y. Y. z beziehungsweise.
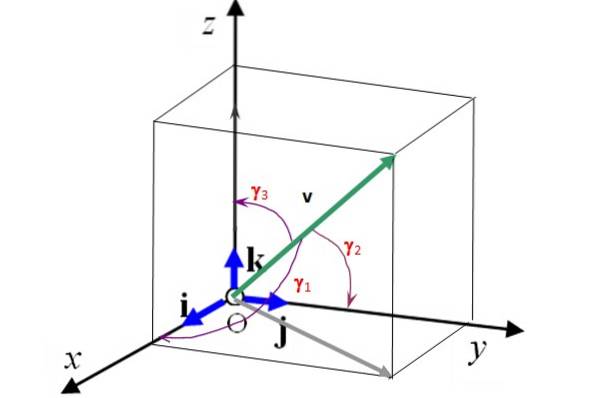
Diese Vektoren stehen senkrecht zueinander und bilden a orthonormale Basis (siehe Abbildung 2). Dies bedeutet, dass ein 3D-Vektor wie folgt geschrieben werden kann:
v = vx ich + vY. j + vz k
Winkel und Richtungskosinus eines Vektors
Fig. 2 zeigt auch die Direktorwinkel γ1, γzwei und γ3 als Vektor v macht jeweils mit den Achsen x, Y. Y. z. Wenn man diese Winkel und die Größe des Vektors kennt, ist er vollständig bestimmt. Darüber hinaus erfüllen die Kosinusse der Direktorwinkel die folgende Beziehung:
(cos γ1)zwei + (cos γzwei)zwei + (cos γ3)zwei = 1
Gelöste Übungen
-Übung 1
In Abbildung 2 sind die Winkel γ1, γzwei und γ3 als Vektor v Die Form des Moduls 50 mit den Koordinatenachsen beträgt jeweils: 75,0º, 60,0º und 34,3º. Finden Sie die kartesischen Komponenten dieses Vektors und stellen Sie sie in Form der Einheitsvektoren dar ich, j Y. k.
Lösung
Vektorprojektion v auf der Achse x ist V.x = 50. cos 75º = 12.941. Ebenso die Projektion von v auf der Achse Y. ist V.Y. = 50 cos 60 º = 25 und schließlich auf der Achse z ist V.z = 50. cos 34,3º = 41,3. Jetzt v kann ausgedrückt werden als:
v = 12,9 ich + 25.0 j + 41.3 k
-Übung 2
Finden Sie die Spannungen in jedem der Kabel, die den Löffel halten, in der Abbildung, die sich im Gleichgewicht befindet, wenn sein Gewicht 30 N beträgt.
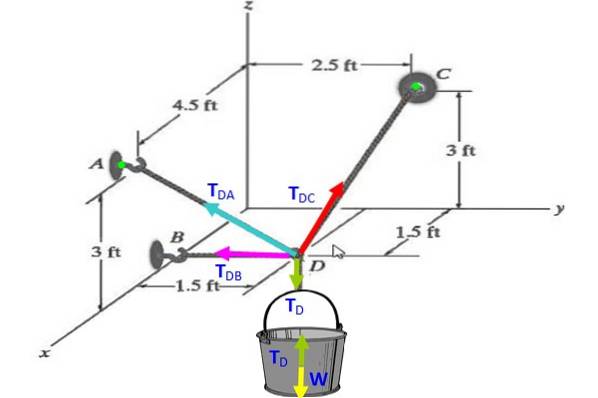
Lösung
Auf dem Eimer zeigt das Freikörperdiagramm dies an T.D. (grün) gleicht das Gewicht aus W. (gelb), daher T.D. = W = 30 N..
Im Knoten der Vektor T.D. ist vertikal nach unten gerichtet, dann:
T.D. = 30 (-k) N..
Gehen Sie folgendermaßen vor, um die verbleibenden Spannungen zu ermitteln:
Schritt 1: Finden Sie die Koordinaten aller Punkte
A = (4,5,0,3) (A liegt in der Ebene der Wand x-z)
B = (1,5,0,0) (B liegt auf der x-Achse)
C = (0, 2,5, 3) (C liegt in der Ebene der Wand und Z.)
D = (1,5, 1,5, 0) (D liegt in der horizontalen Ebene x-y)
Schritt 2: Finden Sie die Vektoren in jeder Richtung, indem Sie die Koordinaten des Endes und des Anfangs subtrahieren
GIBT = <3; -1.5; 3>
DC = <-1.5; 1; 3>
DB = <0; -1.5 ; 0>
Schritt 3: Berechnen Sie Module und Einheitsvektoren
Ein Einheitsvektor wird durch den Ausdruck erhalten: oder = r / r, mit r (in Fettdruck) ist der Vektor und r (nicht in Fettdruck) ist das Modul des Vektors.
DA = (3zwei + (-1,5)zwei + 3zwei)½ = 4,5; DC = ((-1,5) zwei + 1zwei + 3zwei)½ = 3,5
oderGIBT = <3; -1.5; 3>4,5 = <0.67 ; -0.33 ; 0.67>
oderDC = <-1.5; 1; 3>3,5 = <-0.43; 0.29; 0.86>
oderDB = <0; -1; 0>
oderD. = <0; 0; -1>
Schritt 4: Drücken Sie alle Spannungen als Vektoren aus
T.GIBT = T.GIBT oderGIBT = T.GIBT<0.67 ; -0.33 ; 0.67>
T.DC = T.DC oderDC = T.DC <-0.43; 0.29; 0.86>
T.DB = T.DB oderDB = T.DB <0; -1; 0>
T.D. = 30 <0; 0; -1>
Schritt 5: Wenden Sie die statische Gleichgewichtsbedingung an und lösen Sie das Gleichungssystem
Schließlich wird die Bedingung des statischen Gleichgewichts auf den Eimer angewendet, so dass die Vektorsumme aller auf den Knoten einwirkenden Kräfte Null ist:
T.GIBT + T.DC + T.DB + T.D. = 0
Da sich die Spannungen im Raum befinden, ergibt sich für jede Komponente ein System von drei Gleichungen (x, und und z) der Spannungen.
0,67 T.GIBT -0,43 T.DC + 0 T.DB = 0
-0,33 T.GIBT + 0,29 T.DC - T.DB = 0
0,67 T.GIBT + 0,86 T.DC +0 T.DB - 30 = 0
Die Lösung lautet: T.GIBT = 14,9 N; T.GIBT = 23,3 N; T.DB = 1,82 N.
Verweise
- Bedford, 2000. A. Technische Mechanik: Statik. Addison Wesley. 38-52.
- Figueroa, D. Reihe: Physik für Naturwissenschaften und Technik. Band 1. Kinematik. 31-68.
- Körperlich. Modul 8: Vektoren. Wiederhergestellt von: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanik für Ingenieure. Statisch. 6. Auflage. Continental Verlag. 15-53.
- Vektoradditionsrechner. Wiederhergestellt von: 1728.org



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.