
Ordnungsvariable


Was ist eine Ordnungsvariable??
Eine Ordnungsvariable nimmt Werte an, die geordnet werden können (oder eine Reihenfolge bezeichnen). Zum Beispiel kann die variable Größe einer Person klassifiziert werden in: groß, durchschnittlich und klein.
Eine Ordnungsskala beschreibt neben der Identifizierung, Gruppierung und Differenzierung der Lerneinheiten als Nominalvariable auch die Größe und ist daher durch die Reihenfolge gekennzeichnet. Das heißt, die Lerneinheiten können in aufsteigender oder abnehmender Reihenfolge in Bezug auf die Größe geordnet werden.
In dieser Skala sprechen wir von erstem, zweitem, drittem oder hohem, mittlerem, niedrigem; Es ist jedoch kein Maß zwischen den Klassen festgelegt. Zum Beispiel: Die variable Bewertung in einem Test der Zufriedenheit mit einer erbrachten Dienstleistung kann in vier Kategorien gemessen werden: unzufrieden, gleichgültig, zufrieden, sehr zufrieden.
Es kann nach der geäußerten Zufriedenheit bestellt werden, aber es ist nicht bekannt, wie unterschiedlich es von sehr zufrieden zufrieden ist, und es ist auch nicht bekannt, ob der Unterschied zwischen unzufrieden und gleichgültig der gleiche ist wie zwischen zufrieden und sehr zufrieden.
Die Ordnungsskala bezieht sich auf Messungen, bei denen nur "größere", "kleinere" oder "gleiche" Vergleiche zwischen aufeinanderfolgenden Messungen durchgeführt werden. Stellt eine Klassifizierung oder Reihenfolge eines Satzes beobachteter Werte dar.
Konzept und Eigenschaften der Ordnungsvariablen
Auf einer Ordnungsskala werden die Beobachtungen in einer relativen Reihenfolge in Bezug auf das zu bewertende Merkmal angeordnet. Das heißt, die Datenkategorien werden nach dem besonderen Merkmal, das sie besitzen, klassifiziert oder geordnet.
Wenn wir Zahlen verwenden, repräsentiert deren Größe die Reihenfolge des Ranges des beobachteten Attributs. Nur die Beziehungen "größer als", "kleiner als" und "gleich" haben auf einer ordinalen Messskala eine Bedeutung..
Aus mathematischer Sicht und wie Nennskalen unterstützen Ordnungsskalen nur die Berechnung von Proportionen, Prozentsätzen und Verhältnissen.
Das Maß für die zentrale Tendenz, das eine Ordnungsvariable am besten erklärt, ist der Median. Dies ist der Wert, der sich in der Mitte des Datensatzes befindet, der vom niedrigsten zum höchsten geordnet ist.
Wenn Objekte nach einem Merkmal klassifiziert werden, kann festgestellt werden, welches Objekt im Vergleich zu einem anderen mehr oder weniger Merkmale aufweist. aber Sie können den Unterschied nicht quantifizieren.
Zum Beispiel drei Objekte, die unter Berücksichtigung einiger Merkmale als "erstes", "zweites" und "drittes" geordnet wurden. Der zweite Platz unterscheidet sich vom ersten um einen Betrag, der nicht unbedingt dem Betrag entspricht, um den er sich vom dritten Platz unterscheidet.
Beispiele für Ordnungsvariablen

Einige Beispiele für Ordnungsvariablen:
- Soziale Klasse (A - hoch; B - mittel hoch; C - mittel; D - niedrig; E - sehr niedrig).
- Qualitative Schulnoten (I - unzureichend; A - akzeptabel; B - gut; S - ausgezeichnet; E - ausgezeichnet).
- Militärische Ränge (General, Oberst, Oberstleutnant, Major, Kapitän usw.).
- Bildungsabschluss (Grundschule, Gymnasium, professioneller Techniker, Technologe, Universität usw.).
- Entwicklungsstadium eines Menschen (Neugeborenes, Baby, Kind, Junge, Erwachsener, Ältere).
- Filmklassifikation (A - Alle öffentlich; B - über 12 Jahre alt; C - über 18 Jahre alt; D - über 21 Jahre alt).
- Reifung einer Frucht (grün, pintona, reif, sehr reif, faul).
- Grad der Zufriedenheit mit der Erbringung einer öffentlichen Dienstleistung. (Sehr zufrieden; zufrieden; gleichgültig; usw.).
- Beispiele erklärt
Bewertung eines Lehrers durch seine Schüler
Die Schüler eines bestimmten Kurses haben die Möglichkeit, eine Bewertungsumfrage zur pädagogischen Kapazität ihres Lehrers auszufüllen, die mit einer Ordnungsvariablen gemessen wird, deren Skala lautet: 5 - Ausgezeichnet, 4 - Gut, 3 - Durchschnitt, 2 - Schlecht, 1 - Arm.
Die Werte der Variablen sind vom höchsten oder besten zum niedrigsten oder schlechtesten geordnet: ausgezeichnet ist besser als gut, gut ist besser als der Durchschnitt usw. Es ist jedoch nicht möglich, die Größe der Unterschiede zu unterscheiden.
Ist der Unterschied zwischen ausgezeichnet und gut der gleiche wie zwischen schlecht und schlecht? Es ist nicht möglich zu bestätigen.
Wenn wir die Zahlen verwenden, geben sie keine Größe an. Beispielsweise sollte nicht der Schluss gezogen werden, dass die Bewertung Gut (Bewertung 4) doppelt so hoch ist wie die Bewertung Schlecht (Bewertung 2). Es kann nur gesagt werden, dass die gute Bewertung besser ist als die schlechte Bewertung, aber es kann nicht quantifiziert werden, inwieweit sie besser ist..
Akzeptanzniveau einer Mahlzeit
Ein Verkostungswettbewerb bewertet Lebensmittel in einem Kochwettbewerb anhand der Ordnungsvariablen in der Akzeptanzstufe, ausgedrückt in: A - Ausgezeichnet, B - Gut, C - Nicht akzeptabel. Die Verwendung einer Messskala, die von der höchsten zur niedrigsten geordnet ist, ist belegt, es ist jedoch nicht möglich, die Differenz zwischen den Werten der Skala festzustellen.
Wie wird der Gewinner ermittelt, da es sich um einen Wettbewerb handelt? Es scheint am besten geeignet zu sein, Mode zu verwenden, um die Entscheidung über den Gewinner des Wettbewerbs zu treffen. Verstehen Sie den Modus als den Namen, der dem höchsten Wert (dem häufigsten) der Anzahl pro Stufe gegeben wird. Zum Beispiel wurden 5 A, 14 B, 10 C gezählt; Der Modus ist B, da es das Level ist, das die meisten Meinungen hatte.
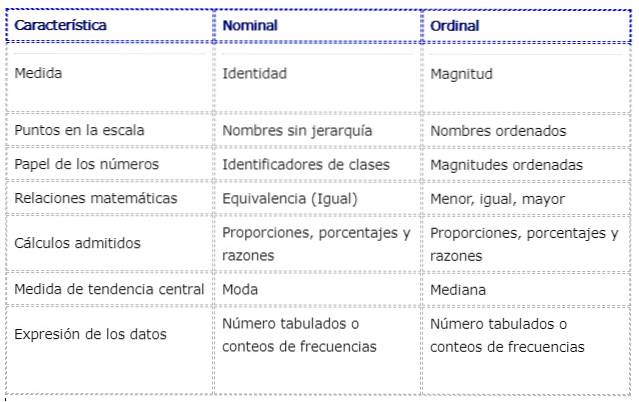
Unterschiede zur Nennvariablen
Die folgende Tabelle zeigt einige Unterschiede und Ähnlichkeiten zwischen den in nominaler und ordinaler Skala gemessenen Variablen:
Verweise
- Freund, R.; Wilson, W.; Mohr, D. (2010). Statistische Methoden. Dritte Auflage. Akademische Presse-Elsevier Inc..
- Glass, G.; Stanley, J. (1996). Statistische Methoden, die nicht auf die Sozialwissenschaften angewendet werden. Prentice Hall Hispanoamericana S. A..
- Süß.; Marchal, W.; Wathen, S. (2012). Statistiken für Wirtschaft und Wirtschaft. Fünfzehnte Ausgabe. McGraw-Hill / Interamericana Herausgeber S. A..
- Orlandoni, G. (2010). Statistische Messskalen. Telos Magazin. Von ojs.urbe.edu wiederhergestellt.
- Siegel, S.; Castellan, N. (1998). Nichtparametrische Statistiken für die Verhaltenswissenschaften. Vierte Ausgabe. Editorial Trillas S. A..
- Wikipedia. (2019). Messniveau. Von en.wikipedia.org wiederhergestellt.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.