Gleichschenklige trapezförmige Eigenschaften, Beziehungen und Formeln, Beispiele

EIN Trapez gleichschenklig ist ein Viereck, in dem zwei der Seiten parallel zueinander sind und auch die zwei Winkel, die an eine dieser parallelen Seiten angrenzen, das gleiche Maß haben.

In Abbildung 1 haben wir das viereckige ABCD, bei dem die Seiten AD und BC parallel sind. Zusätzlich haben die Winkel ∠DAB und ∠ADC neben der parallelen Seite AD das gleiche Maß α. 

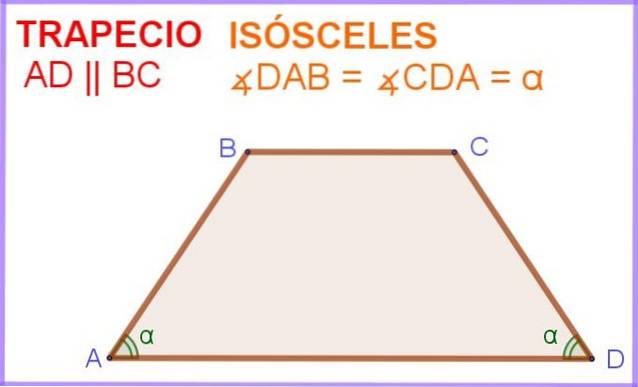
Dieses viereckige oder vierseitige Polygon ist also praktisch ein gleichschenkliges Trapez.

In einem Trapez werden die parallelen Seiten genannt Basen und die Nicht-Parallelen werden aufgerufen seitlich. Ein weiteres wichtiges Merkmal ist das Höhe, Dies ist der Abstand, der die parallelen Seiten trennt.

Neben dem gleichschenkligen Trapez gibt es noch andere Arten von Trapez:

-T.Skalenseeteufel, Das hat all seine verschiedenen Winkel und Seiten.

-T.Rechteck Seeteufel, in dem eine Seite rechts benachbarte Winkel hat.

Die Trapezform ist in verschiedenen Bereichen des Designs, der Architektur, der Elektronik, der Berechnung und vielem mehr üblich, wie später noch zu sehen sein wird. Daher ist es wichtig, sich mit seinen Eigenschaften vertraut zu machen.

Artikelverzeichnis

• 1 Eigenschaften
  • 1.1 Exklusiv des gleichschenkligen Trapezes
  • 1.2 Für alle Trapezoide
• 2 Beziehungen und Formeln
  • 2.1 Einzigartige Beziehungen des gleichschenkligen Trapezes
  • 2.2 Beziehungen für jedes Trapez
  • 2.3 Beziehungen für gleichschenkliges Trapez mit beschriftetem Umfang
  • 2.4 Formeln zur Bestimmung einer Seite, Kenntnis der anderen und eines Winkels
  • 2.5 Bestimmung einer Seite, Kenntnis der anderen und einer Diagonale
  • 2.6 Basis aus Höhe, Fläche und anderer Basis
  • 2.7 Bekannte Seitenbasen, Fläche und Winkel
  • 2.8 Bekannter lateraler Median, Fläche und Winkel
  • 2.9 Bekannte Höhe der Seiten
  • 2.10 Bekannte Höhe ein Winkel und zwei Seiten
  • 2.11 Bekannte Diagonalen auf allen Seiten oder zwei Seiten und ein Winkel
  • 2.12 Umfang des gleichschenkligen Dreiecks 
  • 2.13 Fläche des gleichschenkligen Trapezes
  • 2.14 Radius des umschriebenen Kreises
• 3 Anwendungsbeispiele für das gleichschenklige Trapez
  • 3.1 In Architektur und Bau
  • 3.2 Im Design
• 4 Gelöste Übungen
  • 4.1 - Übung 1
  • 4.2 - Übung 2
• 5 Referenzen

Eigenschaften

Exklusiv für das gleichschenklige Trapez

Wenn ein Trapez gleichschenklig ist, hat es die folgenden charakteristischen Eigenschaften:

1.- Die Seiten haben das gleiche Maß.

2.- Die Winkel neben den Basen sind gleich.

3.- Gegenwinkel sind ergänzend.

4.- Die Diagonalen haben die gleiche Länge, wobei die beiden Segmente, die die gegenüberliegenden Eckpunkte verbinden, gleich sind.

5.- Der Winkel zwischen den Basen und den Diagonalen ist alle gleich groß.

6.- Es hat einen umschriebenen Umfang.

Wenn umgekehrt ein Trapez eine der oben genannten Eigenschaften erfüllt, ist es ein gleichschenkliges Trapez.

Wenn in einem gleichschenkligen Trapez einer der Winkel richtig ist (90 °), sind auch alle anderen Winkel richtig und bilden ein Rechteck. Das heißt, ein Rechteck ist ein besonderer Fall von gleichschenkligem Trapez.

Für alle Trapeze

Die folgenden Eigenschaften gelten für jedes Trapez:

7.- Die Median des Trapezes, dh das Segment, das die Mittelpunkte seiner nicht parallelen Seiten verbindet, ist parallel zu einer der Basen.

8.- Die Länge des Medians entspricht der Halbsumme (Summe geteilt durch 2) der seiner Basen.

9.- Der Median eines Trapezes schneidet seine Diagonalen in der Mitte.

10.- Die Diagonalen eines Trapezes schneiden sich an einem Punkt, der sie in zwei Abschnitte unterteilt, die proportional zu den Quotienten der Basen sind.

11.- Die Summe der Quadrate der Diagonalen eines Trapezes entspricht der Summe der Quadrate seiner Seiten plus dem Doppelprodukt seiner Basen.

12.- Das Segment, das die Mittelpunkte der Diagonalen verbindet, hat eine Länge, die der Halbdifferenz der Basen entspricht.

13.- Die Winkel neben den seitlichen sind ergänzend.

14.- Ein Trapez hat genau dann einen eingeschriebenen Umfang, wenn die Summe seiner Basen gleich der Summe seiner Seiten ist.

15.- Wenn ein Trapez einen eingeschriebenen Umfang hat, sind die Winkel mit einem Scheitelpunkt in der Mitte des Umfangs und die Seiten, die durch die Enden derselben Seite verlaufen, rechte Winkel.

Beziehungen und Formeln

Die folgenden Beziehungen und Formeln beziehen sich auf Abbildung 3, in der neben dem gleichschenkligen Trapez auch andere bereits erwähnte wichtige Segmente wie Diagonalen, Höhe und Median dargestellt sind.

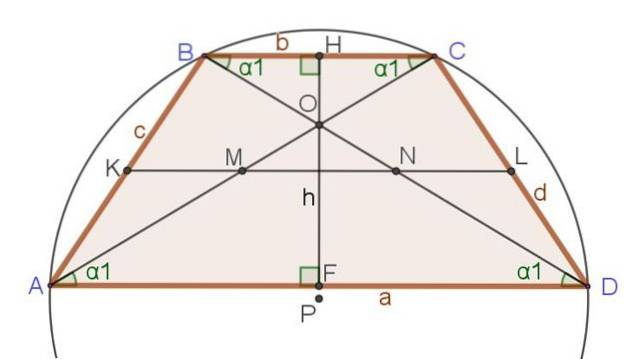
Einzigartige Beziehungen des gleichschenkligen Trapezes

1.- AB = DC = c = d

2.- ∡DAB = ∡CDA und ∡ABC = ∡BCD

3.- ∡DAB + ∡BCD = 180º und ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ADCAD = ∡BDA = ∡CBD = ∡BCA = α₁

6.- A, B, C und D gehören zum umschriebenen Kreis.

Beziehungen für jedes Trapez

7. Wenn AK = KB und DL = LC ⇒ KL || AD und KL || BC

8.- KL = (AD + BC) / 2

9. AM = MC = AC / 2 und DN = NB = DB / 2

10.- AO / OC = AD / BC und DO / OB = AD / BC

11.- AC^zwei + DB^zwei = AB^zwei + DC^zwei + 2⋅AD⋅BC

12.- MN = (AD - BC) / 2

13.- ∡DAB + ∡ABC = 180º und ∡CDA + ∡BCD = 180º

14.- Wenn AD + BC = AB + DC ⇒ ∃ R als äquidistant von AD, BC, AB und DC

15.- Wenn ∃ R gleich weit von AD, BC, AB und DC entfernt ist, dann:

∡BRA = ∡DRC = 90º

Beziehungen für gleichschenkliges Trapez mit beschriftetem Umfang

Wenn in einem gleichschenkligen Trapez die Summe der Basen doppelt so groß ist wie die seitliche, dann existiert der eingeschriebene Umfang.

Die folgenden Eigenschaften gelten, wenn das gleichschenklige Trapez einen beschrifteten Umfang hat (siehe Abbildung 4 oben):

16.- KL = AB = DC = (AD + BC) / 2

17.- Die Diagonalen schneiden sich rechtwinklig: AC ⊥ BD

18.- Die Höhe entspricht dem Median: HF = KL, dh h = m.

19.- Das Quadrat der Höhe ist gleich dem Produkt der Basen: h^zwei = BC⋅AD

20.- Unter diesen spezifischen Bedingungen ist die Fläche des Trapezes gleich dem Quadrat der Höhe oder dem Produkt der Basen: Fläche = h^zwei = BC⋅AD.

Formeln zur Bestimmung einer Seite, zur Kenntnis der anderen und eines Winkels

Bekannt eine Basis, die laterale und ein Winkel, kann die andere Basis bestimmt werden durch:

a = b + 2c Cos α

b = a - 2c Cos α

Wenn die Länge der Basen und ein Winkel als bekannte Daten angegeben werden, sind die Längen beider Seiten:

c = (a - b) / (2 Cos α)

Bestimmung einer Seite, Kenntnis der anderen und einer Diagonale

a = (d₁^zwei - c^zwei) / b;

b = (d₁^zwei - c^zwei) / bis 

c = √ (d₁^zwei - a⋅b)

Wo d₁ ist die Länge der Diagonalen.

Basis aus Höhe, Fläche und anderer Basis

a = (2 A) / h - b

b = (2 A) / h - a

Bekannte Seitenbasen, Fläche und Winkel

c = (2A) / [(a + b) sin α]

Bekannter lateraler Median, Fläche und Winkel

c = A / (m sin α)

Bekannte Höhe der Seiten

h = √ [4 c^zwei - (a - b)^zwei]]

Bekannte Höhe ein Winkel und zwei Seiten

h = tg α⋅ (a - b) / 2 = c. sin α

Bekannte Diagonalen allseitig oder zwei Seiten und ein Winkel

d₁ = √ (c^zwei+ a b)

d₁ = √ (a^zwei+ c^zwei - 2 a c Cos α)

d₁ = √ (b^zwei + c^zwei- 2 b c Cos β)

Umfang des gleichschenkligen Dreiecks 

P = a + b + 2c

Gleichschenkliges Trapezgebiet

Abhängig von den bekannten Daten gibt es verschiedene Formeln zur Berechnung der Fläche. Folgendes ist je nach Basis und Höhe am bekanntesten:

A = h⋅ (a + b) / 2

Und Sie können auch diese anderen verwenden:

-Wenn die Seiten bekannt sind

A = [(a + b) / 4] √ [4c^zwei - (a - b)^zwei]]

-Wenn Sie zwei Seiten und einen Winkel haben

A = (b + c Cosα) c Sen α = (a - c Cos α) c Sen α

-Wenn der Radius des Beschriftungskreises und ein Winkel bekannt sind

A = 4 r^zwei / Sen α = 4 r^zwei / Sen β

-Wenn die Basen und ein Winkel bekannt sind

A = a⋅b / Sen α = a⋅b / Sen β 

-Wenn das Trapez einen Umfang eingeschrieben werden kann

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2

-Bekannt die Diagonalen und den Winkel, den sie miteinander bilden

A = (d₁^zwei/ 2) Sen γ = (d₁^zwei / 2) Sen δ 

-Wenn Sie die laterale, den Median und einen Winkel haben

A = mc.sen α = mc.sen β

Radius des umschriebenen Kreises

Nur gleichschenklige Trapezoide haben einen umschriebenen Umfang. Wenn die größere Basis a, die laterale c und die Diagonale d bekannt sind₁, dann ist der Radius R des Kreises, der durch die vier Eckpunkte des Trapezes verläuft ,:

R = a⋅c⋅d₁ / 4√ [p (p - a) (p - c) (p - d₁)]

Wobei p = (a + c + d₁) / zwei

Beispiele für die Verwendung des gleichschenkligen Trapezes

Das gleichschenklige Trapez erscheint im Bereich des Designs, wie in Abbildung 2 dargestellt. Und hier einige zusätzliche Beispiele:

In Architektur und Bau

Die alten Inkas kannten das gleichschenklige Trapez und verwendeten es als Bauelement in diesem Fenster in Cuzco, Peru:

Und hier erscheint das Trapez wieder im Anruf Trapezblatt, ein Material, das häufig im Bauwesen verwendet wird:

Im Design

Wir haben bereits gesehen, dass das gleichschenklige Trapez in Alltagsgegenständen vorkommt, einschließlich Lebensmitteln wie diesem Schokoriegel:

Gelöste Übungen

- Übung 1

Ein gleichschenkliges Trapez hat eine Basis von mehr als 9 cm, eine Basis von weniger als 3 cm und seine Diagonalen von jeweils 8 cm. Berechnung:

a) Seite

b) Höhe

c) Umfang

d) Fläche

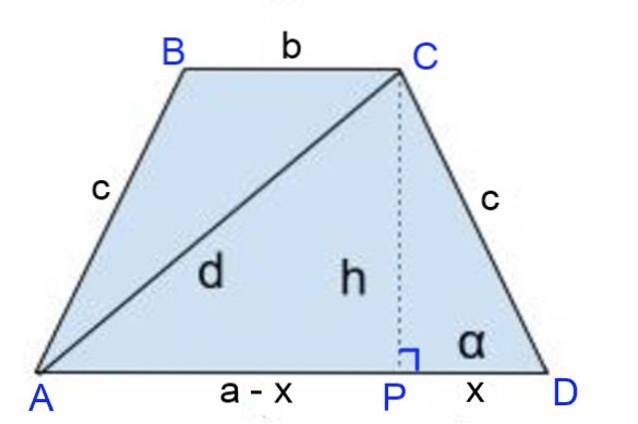
Lösung für

Die Höhe CP = h ist aufgetragen, wobei der Fuß der Höhe die Segmente definiert:

PD = x = (a-b) / 2 y 

AP = a - x = a - a / 2 + b / 2 = (a + b) / 2.

Verwenden des Satzes von Pythagoras zum rechtwinkligen Dreieck DPC:

c^zwei = h^zwei + (a - b)^zwei / 4

Und auch zum rechtwinkligen Dreieck APC:

d^zwei = h^zwei + AP^zwei = h^zwei + (a + b)^zwei / 4

Schließlich wird Mitglied für Mitglied die zweite Gleichung von der ersten subtrahiert und vereinfacht:

d^zwei - c^zwei = ¼ [(a + b)^zwei - (a-b)^zwei] = ¼ [(a + b + a-b) (a + b-a + b)]

d^zwei - c^zwei = ¼ [2a 2b] = a b

c^zwei= d^zwei - a b ⇒ c = √ (d^zwei - a b) = √ (8^zwei - 9⋅3) = √37 = 6,08 cm

Lösung b

h^zwei = d^zwei - (a + b)^zwei / 4 = 8^zwei - (12^zwei / zwei^zwei ) = 8^zwei - 6^zwei = 28

h = 2 √7 = 5,29 cm

Lösung c

Umfang = a + b + 2 c = 9 + 3 + 2 · 6,083 = 24,166 cm

Lösung d

Fläche = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 cm

- Übung 2

Es gibt ein gleichschenkliges Trapez, dessen größte Basis doppelt so klein ist und dessen kleinste Basis der Höhe von 6 cm entspricht. Entscheiden:

a) Die Länge der Seite

b) Umfang

c) Fläche

d) Winkel

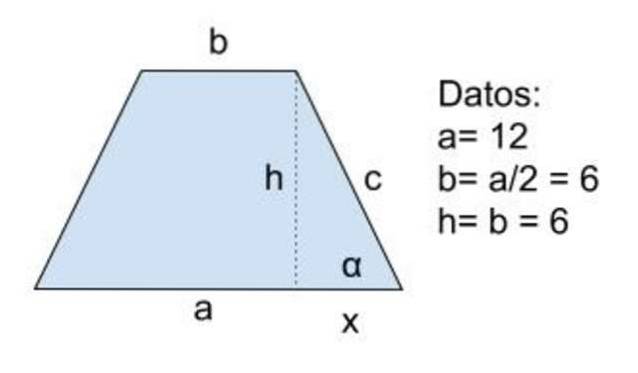
Lösung für

Daten: a = 12, b = a / 2 = 6 und h = b = 6

Wir gehen folgendermaßen vor: Die Höhe h wird gezeichnet und der Satz von Pythagoras wird auf das Hypotenusendreieck „c“ und die Beine h und x angewendet:

c^zwei = h^zwei+xc^zwei

Dann müssen Sie den Wert der Höhe aus den Daten (h = b) und dem des Beins x berechnen: 

a = b + 2 x ⇒ x = (a-b) / 2

Durch Ersetzen der vorherigen Ausdrücke haben wir:

c^zwei = b^zwei+(a-b)^zwei/zwei^zwei

Nun werden die numerischen Werte eingeführt und es wird vereinfacht:

c^zwei = 62+ (12-6) 2/4

c^zwei = 62 (1 + ¼) = 62 (5/4)

Erhalten:

c = 3 √ 5 = 6,71 cm

Lösung b

Der Umfang P = a + b + 2 c

P = 12 + 6 + 6 √ 5 = 6 (8 + √ 5) = 61,42 cm

Lösung c

Die Fläche in Abhängigkeit von Höhe und Länge der Basen beträgt:

A = h · (a + b) / 2 = 6 · (12 + 6) / 2 = 54 cm^zwei

Lösung d

Der Winkel α, der von der Seite mit der größeren Basis gebildet wird, wird durch Trigonometrie erhalten:

Tan (α) = h / x = 6/3 = 2

α = ArcTan (2) = 63,44º

Der andere Winkel, der mit der kleineren Basis das Lateral bildet, ist β, das zu α komplementär ist:

β = 180º - α = 180º - 63,44º = 116,56º

Verweise

1. E. A. 2003. Elemente der Geometrie: mit Übungen und Kompassgeometrie. Universität von Medellin.
2. Campos, F. 2014. Mathematik 2. Grupo Editorial Patria.
3. Freed, K. 2007. Entdecken Sie Polygone. Benchmark Education Company.
4. Hendrik, V. 2013. Verallgemeinerte Polygone. Birkhäuser.
5. IGER. Mathematik Erstes Semester Tacaná. IGER.
6. Jr. Geometrie. 2014. Polygone. Lulu Press, Inc..
7. Miller, Heeren & Hornsby. 2006. Mathematik: Argumentation und Anwendungen. 10 .. Auflage. Pearson Ausbildung.
8. Patiño, M. 2006. Mathematik 5. Editorial Progreso.
9. Wikipedia. Trapez. Wiederhergestellt von: es.wikipedia.com