
Formelarbeit, Einheiten, Beispiele, Übungen

Das Job In der Physik ist es die Übertragung von Energie, die von einer Kraft ausgeführt wird, wenn sich das Objekt, auf das sie einwirkt, bewegt. Mathematisch nimmt es die Form des Skalarprodukts zwischen den Kraftvektoren an F. und Verschiebung s.
Und da das Skalarprodukt zwischen zwei senkrechten Vektoren Null ist, kommt es vor, dass die Kräfte, die sich mit der Verschiebung um 90 ° bilden, gemäß der Definition nicht funktionieren, da:
W = F. ● s = F⋅ s⋅ cos θ
Wo W Arbeit bedeutet, aus dem englischen Wort Arbeit.
Der Vorteil der Definition der Arbeit besteht darin, dass es sich um einen Skalar handelt, dh keine Richtung oder keinen Sinn hat, sondern nur ein Modul und die jeweilige Einheit. Dies erleichtert die Durchführung von Berechnungen mit Energieänderungen, die durch die Einwirkung von Kräften verursacht werden..
Schwerkraft und kinetische Reibung sind Beispiele für Kräfte, die häufig auf sich bewegende Objekte wirken. Eine andere übliche Kraft ist die normale Kraft, die von einer Oberfläche ausgeübt wird, aber im Gegensatz zu diesen wirkt sie niemals auf Objekte, da sie senkrecht zur Verschiebung ist..
Wenn ein Körper frei fällt, wirkt sich die Schwerkraft positiv auf das Handy aus, wodurch es seine Geschwindigkeit beim Fallen erhöht. Andererseits hat kinetische Reibung einen völlig entgegengesetzten Effekt, da sie, da sie sich immer der Bewegung widersetzt, negative Arbeit leistet, die sie nicht begünstigt..
Artikelverzeichnis
- 1 Formeln und Sonderfälle
- 1.1 Arbeit mit variablen Kräften
- 2 Arbeitseinheiten
- 2.1 Einheiten im britischen System
- 2.2 Andere Arbeitseinheiten
- 3 Arbeitsbeispiele
- 3.1 Auf- und Abstieg von Objekten
- 3.2 Punktladungen in elektrischen Feldern
- 3.3 Reibung zwischen Oberflächen
- 3.4 Drücken und ziehen
- 3.5 Kraft in eine Riemenscheibe
- 3.6 Normalkräfte oder Stützen
- 3.7 Magnetkraft
- 3.8 Gegenstände, die an ein Seil gebunden sind
- 3.9 Satelliten im Orbit
- 3.10 Masse-Feder-System
- 4 Übung gelöst
- 5 Referenzen
Formeln und Sonderfälle
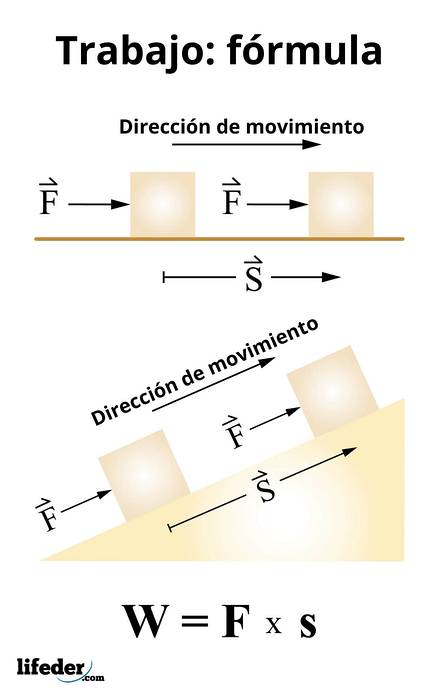
Die Arbeit wird berechnet durch:
W = F. ● s
Dieser Ausdruck gilt für konstante Kräfte und entspricht gemäß der Definition eines Skalarprodukts:
W = F. s. cos θ
Wobei θ der Winkel zwischen der Kraft und der Verschiebung ist. Daraus folgt, dass nur diejenigen Kräfte, die eine Komponente in Verschiebungsrichtung haben, auf einen Körper wirken können.
Und es wird auch klar, dass es auch keine Arbeit gibt, wenn es keine Bewegung gibt.
Was das Vorzeichen betrifft, kann die Arbeit positiv, negativ oder null sein. Wenn die Kraft eine Komponente parallel zur Bewegung hat, hängt das Vorzeichen der Arbeit vom Wert von cos θ ab.
Es gibt einige besondere Fälle, die eine Überlegung wert sind:
- Wenn die Kraft parallel zur Verschiebung ist, ist der Winkel zwischen F. Y. s ist 0º, daher ist die von der Kraft geleistete Arbeit positiv und ihr Wert ist maximal:
W = F⋅s cos 0º = F⋅s
- Wenn die Kraft der Verschiebung entgegenwirkt, dann der Winkel zwischen F. Y. s ist 180º, die von F geleistete Arbeit ist negativ und minimal:
W = F⋅s cos 180º = -F⋅s
- Schließlich gibt es den zuvor erwähnten Fall: wenn der Winkel gebildet durch F. Y. s ist 90º, da cos 90º = 0 ist, ist die Arbeit null:
W = F⋅s cos 90º = 0
Arbeit mit variablen Kräften
Manchmal ist die aufgebrachte Kraft nicht konstant; In diesem Fall müssen Sie auf die Berechnung zurückgreifen, um die geleistete Arbeit zu finden. Zunächst wird ein Arbeitsdifferential dW bestimmt, das an einer infinitesimalen Verschiebung d durchgeführt wirds::
dW = F⋅ds
Um den Wert der Gesamtarbeit zu ermitteln, die diese Kraft leistet, wenn das Objekt von Punkt A nach Punkt B wechselt, müssen beide Seiten wie folgt integriert werden:
Arbeitseinheiten
Die Einheit für die Arbeit im internationalen System ist das Joule, abgekürzt J. Die Einheit hat ihren Namen vom englischen Physiker James Prescott Joule, einem Pionier in der Erforschung der Thermodynamik..
Aus der Arbeitsgleichung wird das Joule als 1 Newton pro Meter definiert:
1 J = 1 Nm
Einheiten im britischen System
Arbeit entspricht als Einheit Pfundkraft x Fuß, manchmal anrufen Pfund-Kraft Fuß. Es ist auch eine Einheit für Energie, aber es muss daran erinnert werden, dass die Arbeit an einem Körper seinen Energiezustand ändert und dass daher Arbeit und Energie gleichwertig sind. Kein Wunder, dass sie die gleichen Laufwerke haben.
Die Äquivalenz zwischen dem Pfundkraftfuß und dem Joule ist wie folgt:
1 Fuß-Pfund-Kraft = 1,35582 J.
Eine bekannte Einheit für Arbeit und Energie, insbesondere für den Bereich Kühlung und Klimatisierung, ist die BTU oder British Thermal Unit.
1 BTU entspricht 1055 J und 778.169 Fuß-Pfund-Kraft.
Andere Einheiten für die Arbeit
Es gibt andere Arbeitseinheiten, die in bestimmten Bereichen der Physik und Technik eingesetzt werden. Unter ihnen haben wir:
Erg
Bezeichnet als Erg, ist die Arbeitseinheit im Cegesimalsystem und entspricht 1 dyna⋅cm oder 1 x 10-7 J..
Elektronenvolt
Das abgekürzte eV wird üblicherweise in der Teilchenphysik verwendet und ist definiert als die Energie, die ein Elektron erhält, wenn es sich durch eine Potentialdifferenz von 1 V bewegt.
Kilowattstunde (kWh)
Es erscheint häufig auf Stromrechnungen. Dies ist die Arbeit, die während einer Stunde von einer Quelle ausgeführt wird, deren Leistung 1 kW beträgt, was 3,6 x 10 entspricht6 J..
Kalorie
Es hängt normalerweise mit der Energie von Lebensmitteln zusammen, obwohl in diesem Zusammenhang tatsächlich auf a Bezug genommen wird Kilokalorie, das sind 1000 Kalorien. Tatsächlich gibt es mehrere Einheiten, die diesen Namen erhalten, daher muss der Kontext sehr gut angegeben werden.
Die Äquivalenz zwischen dem Joule und 1 thermochemische Kalorien es ist:
1 Kalorie = 4,1840 J.
Arbeitsbeispiele
Auf- und Abstieg von Objekten
Wenn Körper entweder vertikal oder eine Rampe hinunter absteigen, wirkt sich das Gewicht positiv aus und begünstigt die Bewegung. Wenn ein Objekt aufsteigt, wirkt die Schwerkraft negativ.
Punktladungen in elektrischen Feldern
Ein gleichmäßiges elektrisches Feld wirkt auf eine Punktladung, die sich in ihm bewegt. Je nach Feld und Vorzeichen der Ladung kann diese Arbeit negativ oder positiv sein.
Reibung zwischen Oberflächen
Kinetische Reibung zwischen Oberflächen wirkt sich immer negativ auf das sich bewegende Objekt aus.
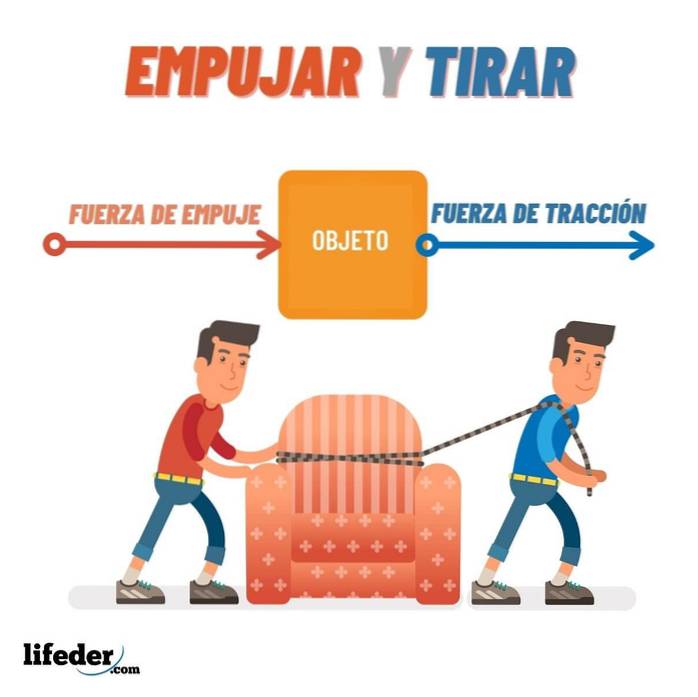
Drücken und Ziehen

Schieben ist eine Kraft, die ein Objekt von etwas wegzieht. Ziehen ist eine Kraft, die ein Objekt dazu bringt, sich näher zu bringen.
Kraft in eine Riemenscheibe
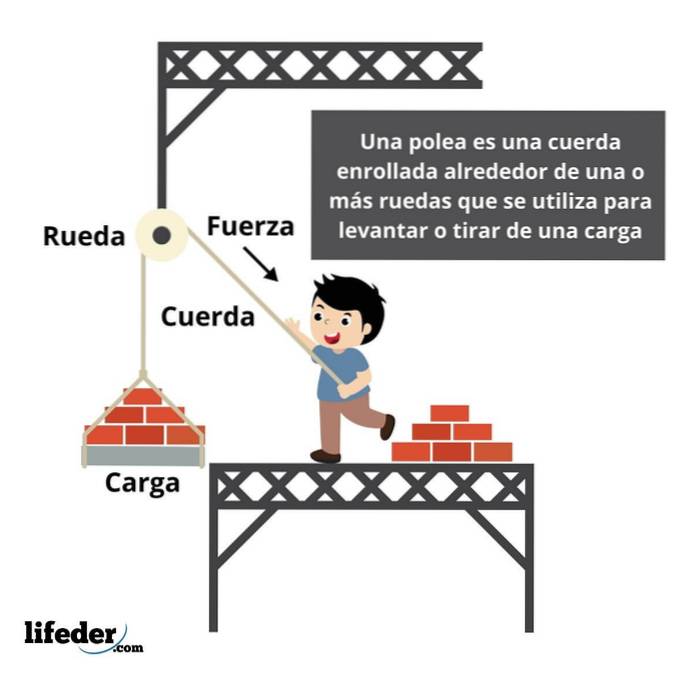
Eine Riemenscheibe ist ein System, mit dem eine Kraft von einem ihrer Enden übertragen wird. In einer einfachen Riemenscheibe muss zum Anheben der Last eine Kraft ausgeübt werden, die dem vom Objekt ausgeübten Widerstand entspricht.
Normalkräfte oder Stützen
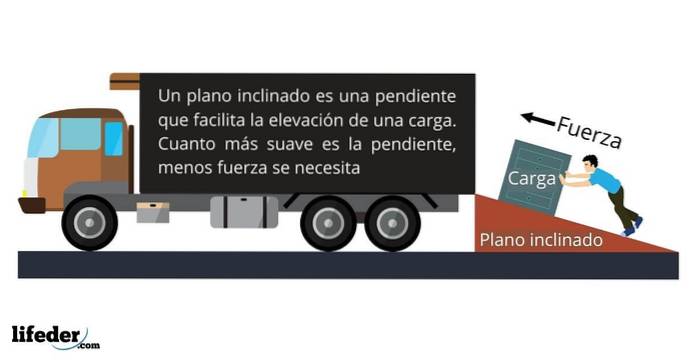
Wie oben erwähnt, funktioniert die Normale Null, wenn sich ein auf einer Oberfläche ruhendes Objekt darauf bewegt, selbst wenn die Oberfläche nicht flach oder geneigt ist..
Magnetkraft
Eine andere Kraft, die keine Arbeit leistet, ist die Magnetkraft, die ein gleichmäßiges Feld auf das geladene Teilchen ausübt, das senkrecht dazu steht. Die Bewegung des Partikels stellt sich als gleichmäßige Kreisbewegung mit der Kraft in radialer Richtung heraus. Da die Verschiebung senkrecht zur Kraft ist, wirkt sie nicht auf die Last..
Gegenstände an einem Seil gebunden
Ein Seil arbeitet auch nicht an einem hängenden Pendel, da die Spannung darin immer senkrecht zur Verschiebung der Masse ist..
Satelliten im Orbit
Die Schwerkraft funktioniert aus dem gleichen Grund wie in den vorherigen Fällen auch nicht auf einem Satelliten in kreisförmiger Umlaufbahn: Sie ist senkrecht zur Verschiebung..
Masse-Feder-System
In einem Masse-Feder-System ist die Kraft F. dass die Feder auf die Masse wirkt, hat Größe F = kx, wo k ist die Federkonstante und x seine Kompression oder Dehnung. Es ist eine variable Kraft, daher hängt die Arbeit davon ab, wie stark sich die Feder dehnt oder schrumpft.
Übung gelöst
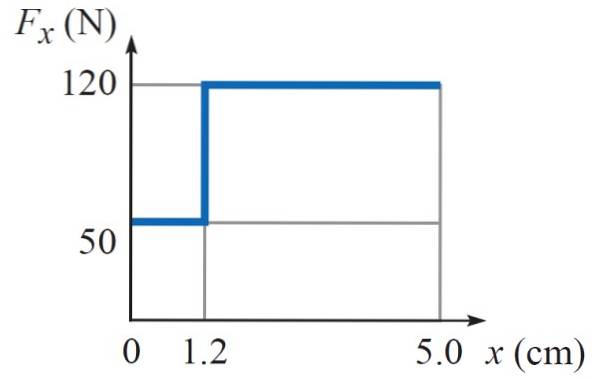
Die folgende Grafik zeigt die Arbeit einer variablen Kraft F.x das hängt von der Position ab x. Dies ist die Kraft, die ein Hammer auf einen Nagel ausübt. Der erste Teil ist die Kraft, die verwendet wird, um den weicheren Abschnitt der Wand festzunageln, und der zweite Teil, um das Eintreiben des Nagels zu beenden.
Wie viel Arbeit muss der Hammer leisten, damit der Nagel insgesamt 5 cm in die Wand sinkt?
Lösung
Die vom Hammer ausgeübte Kraft ist variabel, da weniger Intensität (50 N) erforderlich ist, um den Nagel 1,2 cm in den weichen Teil der Wand zu treiben, während im härteren Teil 120 N erforderlich sind, um den Nagel auf 5 abzusinken cm tief, wie in der Tabelle gezeigt.
In diesem Fall ist die Arbeit das Integral:

Wobei A = 0 cm und B = 5 cm. Da das Integral die Fläche unter dem Graphen Fx vs x ist, reicht es aus, diese Fläche zu finden, die zwei Rechtecken entspricht, das erste mit einer Höhe von 50 N und einer Breite von 1,2 cm und das zweite mit einer Höhe von 120 N und einer Breite (5 cm) - 1,2 cm) = 3,8 cm.
Beide werden berechnet und addiert, um die Gesamtarbeit zu erhalten:
B = 50 N × 1,2 cm + 120 N × 3,8 cm = 516 N cm = 516 N × 0,01 m = 5,16 J..
Verweise
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 2. Dynamik. Herausgegeben von Douglas Figueroa (USB).
- Giambattista, A. 2010. Physik. 2 .. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1. Pearson.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.
- Zapata, F. Mechanische Arbeit. Wiederhergestellt von: francesphysics.blogspot.com.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.