Grundsatz des arithmetischen Beweises, Anwendungen, Übungen

Das Der Grundsatz der Arithmetik gibt an, dass jede natürliche Zahl größer als 1 als Produkt von Primzahlen zerlegt werden kann - einige können wiederholt werden - und diese Form ist für diese Zahl eindeutig, obwohl die Reihenfolge der Faktoren unterschiedlich sein kann.

Denken Sie daran, dass eine Primzahl p Es ist diejenige, die sich nur selbst und 1 als positive Teiler zulässt. Die folgenden Zahlen sind Primzahlen: 2, 3, 5, 7, 11, 13 usw., da es Unendlichkeiten gibt. Die Zahl 1 wird nicht als Primzahl betrachtet, da sie einen einzelnen Teiler hat.

Die Nummern, die nicht den oben genannten Anforderungen entsprechen, werden aufgerufen zusammengesetzte Zahlen, als 4, 6, 8, 9, 10, 12, 14 ... Nehmen wir zum Beispiel die Zahl 10 und sehen sofort, dass sie als Produkt von 2 und 5 zerlegt werden kann:

10 = 2 × 5

Sowohl 2 als auch 5 sind effektiv Primzahlen. Der Satz besagt, dass dies für jede Zahl n möglich ist:

Wo p₁, p_zwei, p₃... p_r sind Primzahlen und k₁, k_zwei, k₃,... k_r Sie sind natürliche Zahlen. Die Primzahlen wirken also wie die Bausteine, aus denen durch Multiplikation die natürlichen Zahlen aufgebaut werden.

Artikelverzeichnis

• 1 Beweis des Fundamentalsatzes der Arithmetik
  • 1.1 Eindeutigkeit der Primfaktorisierung
• 2 Anwendungen
  • 2.1 Primzahlen in der Natur
  • 2.2 Primzahlen und Online-Shopping
• 3 Gelöste Übungen
  • 3.1 - Übung 1
  • 3.2 - Übung 2
• 4 Referenzen

Beweis des Fundamentalsatzes der Arithmetik

Wir beginnen damit zu zeigen, dass jede Zahl in Primfaktoren zerlegt werden kann. Sei eine natürliche Zahl n> 1, Primzahl oder zusammengesetzt.

Wenn beispielsweise n = 2 ist, kann dies ausgedrückt werden als: 2 = 1 × 2, was eine Primzahl ist. Fahren Sie auf die gleiche Weise mit den folgenden Zahlen fort:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Wir fahren so fort und zerlegen alle natürlichen Zahlen, bis wir die Zahl n -1 erreichen. Mal sehen, ob wir es mit der folgenden Nummer schaffen: n.

Wenn n eine Primzahl ist, können wir es als n = 1 × n zerlegen, aber nehmen wir an, dass n zusammengesetzt ist und einen Divisor d hat, logischerweise kleiner als n:

1< d < n.

Wenn n / d = p₁, mit P₁ eine Primzahl, dann wird n geschrieben als:

n = p₁.d

Wenn d eine Primzahl ist, gibt es nichts mehr zu tun, aber wenn dies nicht der Fall ist, gibt es eine Zahl n_zwei Das ist ein Teiler von d und weniger als dieser: n_zwei < d, por lo que d podrá escribirse como el producto de n_zwei durch eine andere Primzahl p_zwei::

d = p_zwei n_zwei

Das beim Einsetzen in die ursprüngliche Zahl n würde ergeben:

n = p₁ .p_zwei .n_zwei

Nehmen wir nun an, dass n_zwei entweder ist eine Primzahl und wir schreiben sie als Produkt einer Primzahl p₃, von einem Teiler von dir n₃, so dass n₃ < n_zwei < n₁ < n:

n_zwei = p₃.n₃ → n = p₁ p_zwei p₃.n₃

 Wir wiederholen diesen Vorgang eine endliche Anzahl von Malen, bis wir erhalten:

n = p₁.p_zwei.p₃ ... p_r

Dies bedeutet, dass es möglich ist, sich zu zersetzen jeder ganze Zahlen von 2 bis n als Produkt von Primzahlen.

Einzigartigkeit der Primfaktorisierung

Lassen Sie uns nun überprüfen, ob diese Zerlegung bis auf die Reihenfolge der Faktoren eindeutig ist. Angenommen, n kann auf zwei Arten geschrieben werden:

n = p₁.p_zwei.p₃ ... p_r = q_1.Was_zwei.Was₃... was_s  (mit r ≤ s)

Natürlich das₁, Was_zwei, Was₃... sind auch Primzahlen. Wie p₁ dividiere a (q_1.Was_zwei.Was₃... was_s) Dann p₁ ist gleich einem der "q", es spielt keine Rolle zu dem, so können wir sagen, dass p₁ = q₁. Wir teilen n durch p₁ und wir bekommen:

p_zwei.p₃ ... p_r =_.Was_zwei.Was₃... was_s

Wir wiederholen den Vorgang, bis wir alles durch p teilen_r, dann bekommen wir:

1 = q_{r + 1}... was_s

Aber es ist nicht möglich, an was zu kommen_{r + 1}... was_s = 1 wenn r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Anwendungen

Wie wir bereits gesagt haben, repräsentieren die Primzahlen, wenn Sie so wollen, die Atome der Zahlen, ihre Grundkomponenten. Der Grundsatz der Arithmetik hat also zahlreiche Anwendungen, die offensichtlichste: Wir können leichter mit großen Zahlen arbeiten, wenn wir sie als Produkt kleinerer Zahlen ausdrücken..

Auf die gleiche Weise können wir das größte gemeinsame Vielfache (LCM) und den größten gemeinsamen Teiler (GCF) finden, ein Verfahren, das uns hilft, Bruchensummen leichter zu bilden, Wurzeln großer Zahlen zu finden oder mit Radikalen zu operieren, zu rationalisieren und Anwendungsprobleme unterschiedlichster Art lösen.

Darüber hinaus sind Primzahlen äußerst rätselhaft. Ein Muster ist in ihnen noch nicht erkannt und es ist nicht möglich zu wissen, welches das nächste sein wird. Der bisher größte wurde von Computern gefunden und hat 24.862.048 Ziffern, obwohl die neuen Primzahlen jedes Mal weniger häufig erscheinen.

Primzahlen in der Natur

Die Zikaden, Zikaden oder Zikaden, die im Nordosten der Vereinigten Staaten leben, entstehen in Zyklen von 13 oder 17 Jahren. Sie sind beide Primzahlen.

Auf diese Weise vermeiden die Zikaden, dass sie mit Raubtieren oder Konkurrenten zusammenfallen, die andere Geburtsperioden haben, und die verschiedenen Zikadensorten konkurrieren auch nicht miteinander, da sie nicht im selben Jahr zusammenfallen..

Primzahlen und Online-Shopping

In der Kryptographie werden Primzahlen verwendet, um Kreditkartendaten beim Einkauf über das Internet geheim zu halten. Auf diese Weise gelangen die Daten, die der Käufer genau im Geschäft ankommt, ohne verloren zu gehen oder in die Hände skrupelloser Personen zu fallen..

Wie? Die Daten auf den Karten sind in einer Zahl N codiert, die als Produkt von Primzahlen ausgedrückt werden kann. Diese Primzahlen sind der Schlüssel, den die Daten enthüllen, aber sie sind der Öffentlichkeit unbekannt. Sie können nur in dem Web dekodiert werden, an das sie gerichtet sind.

Das Zerlegen einer Zahl in Faktoren ist eine einfache Aufgabe, wenn die Zahlen klein sind (siehe die gelösten Übungen). In diesem Fall werden jedoch Primzahlen mit 100 Ziffern als Schlüssel verwendet, die beim Multiplizieren viel größere Zahlen ergeben, deren detaillierte Zerlegung a beinhaltet große Aufgabe.

Gelöste Übungen

- Übung 1

Zerlegen Sie 1029 in Primfaktoren.

Lösung

1029 ist durch 3 teilbar. Es ist bekannt, dass beim Addieren seiner Ziffern die Summe ein Vielfaches von 3: 1 + 0 + 2 + 9 = 12 ist. Da die Reihenfolge der Faktoren das Produkt nicht verändert, können wir dort beginnen:

1029 3

343

1029 = 3 × 343

Andererseits ist 343 = 7³, dann:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

Und da sowohl 3 als auch 7 Primzahlen sind, ist dies die Zerlegung von 1029.

- Übung 2

Faktor das Trinom x^zwei + 42x + 432.

Lösung

Das Trinom wird in der Form (x + a) umgeschrieben. (x + b) und wir müssen die Werte von a und b finden, so dass:

a + b = 42; a.b = 432

Die Zahl 432 wird in Primfaktoren zerlegt und von dort wird die geeignete Kombination durch Versuch und Irrtum ausgewählt, so dass die hinzugefügten Faktoren 42 ergeben.

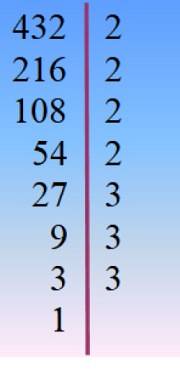
432 = 2⁴ × 3³ = 2 × 3³× 2³ = 2⁴× 3^zwei × 3 =…

Von hier aus gibt es mehrere Möglichkeiten, 432 zu schreiben:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

Und alle können durch Kombinieren von Produkten zwischen den Primfaktoren gefunden werden. Um die vorgeschlagene Übung zu lösen, ist die einzig geeignete Kombination: 432 = 24 × 18, da 24 + 18 = 42, dann:

x^zwei + 42x + 432 = (x + 24). (x +18)

Verweise

1. Baldor, A. 1986. Theoretische praktische Arithmetik. Compañía Cultural Editora de Textos Americanos S.A..
2. BBC World. Der verborgene Code der Natur. Wiederhergestellt von: bbc.com.
3. De Leon, Manuel Primzahlen: die Hüter des Internets. Wiederhergestellt von: blogs.20minutos.es.
4. UNAM. Zahlentheorie I: Fundamentalsatz der Arithmetik. Wiederhergestellt von: teoriadenumeros.wikidot.com.
5. Wikipedia. Der Grundsatz der Arithmetik. Wiederhergestellt von: es.wikipedia.org.