
Varignons Satz

Was ist der Satz von Varignon??
Der Satz von Varignon in der Mechanik besagt, dass die Summe der Momente, die von einem System gleichzeitiger Kräfte in Bezug auf einen bestimmten Punkt erzeugt werden, gleich dem Moment der resultierenden Kraft in Bezug auf denselben Punkt ist.
Aus diesem Grund wird dieser Satz auch als bezeichnet der Beginn von Momenten.
Obwohl der Holländer Simon Stevin (1548-1620), der Schöpfer des hydrostatischen Paradoxons, der erste war, der es aussprach, war der französische Mathematiker Pierre Varignon (1654-1722) derjenige, der ihm später seine endgültige Form gab.
Ein Beispiel für die Funktionsweise von Varignons Theorem in der Mechanik ist das folgende: Angenommen, ein einfaches System aus zwei koplanaren und gleichzeitigen Kräften wirkt auf einen Punkt F.1 Y. F.zwei, (wegen ihres Vektorzeichens fett gedruckt). Diese Kräfte erzeugen eine Netto- oder resultierende Kraft, die genannt wird F.R..
Jede Kraft übt ein Drehmoment oder Moment um einen Punkt O aus, der durch das Vektorprodukt zwischen dem Positionsvektor berechnet wird rOP und die Stärke F., wo rOP ist von O bis zum Punkt der Parallelität P gerichtet:
M.O1 = rOP × F.1
M.O2 = rOP × F.zwei
Angenommen F.R. = F.1 + F.zwei, dann:
M.ODER = rOP × F.1 + rOP × F.zwei = M.O1 + M.O2
Aber wie rOP ist daher ein gemeinsamer Faktor beim Anwenden von Verteilungseigenschaften auf das Kreuzprodukt:
M.ODER = rOP × ((F.1 + F.zwei) = rOP × F.R.
Daher entspricht die Summe der Momente oder Drehmomente jeder Kraft in Bezug auf Punkt O dem Moment der resultierenden Kraft in Bezug auf denselben Punkt.
Aussage und Beweis
Sei ein System von N gleichzeitigen Kräften, gebildet durch F.1, F.zwei, F.3... F.N., deren Wirkungslinien schneiden sich am Punkt P (siehe Abbildung 1), dem Moment dieses Kraftsystems M.ODER, in Bezug auf einen Punkt O ist gegeben durch:
M.ODER = rOP × F.1 + rOP × F.zwei + rOP × F.3 +... rOP × F.N. = rOP × ((F.1 + F.zwei + F.3 +... F.N.)
Demonstration
Um den Satz zu beweisen, wird die Verteilungseigenschaft des Vektorprodukts zwischen Vektoren verwendet.
Seid die Kräfte F.1, F.zwei, F.3... F.N. angewendet auf Punkte A.1, ZUzwei, ZU3… ZUN. und gleichzeitig am Punkt P. Das resultierende Moment dieses Systems in Bezug auf einen Punkt O, genannt M.ODER, ist die Summe der Momente jeder Kraft in Bezug auf diesen Punkt:
M.ODER = ∑ rOAi × F.ich
Wobei die Summe von i = 1 nach i = N geht, da es N Kräfte gibt. Da es sich um gleichzeitige Kräfte handelt und das Vektorprodukt zwischen parallelen Vektoren Null ist, geschieht Folgendes:
rPAi × F.ich = 0
Mit dem Nullvektor bezeichnet als 0.
Das Moment einer der Kräfte in Bezug auf O, zum Beispiel das der Kraft F.ich angewendet in A.ich, es ist so geschrieben:
M.Ich hörte = rOAi × F.ich
Der Positionsvektor rOAi kann als die Summe von zwei Positionsvektoren ausgedrückt werden:
rOAi = rOP + rPAi
Auf diese Weise wird der Moment um O der Kraft F.ich es ist:
M.Ich hörte = (rOP + rPAi) × F.ich = (rOP × F.ich) + (rPAi × F.ich)
Aber der letzte Term ist null, wie oben erklärt, weil rPAi ist auf der Linie der Aktion von F.ich, So:
M.Ich hörte = rOP × F.ich
Zu wissen, dass das Moment des Systems in Bezug auf Punkt O die Summe aller einzelnen Momente jeder Kraft in Bezug auf diesen Punkt ist, dann:
M.ODER = ∑ M.Ich hörte = ∑ rOP × F.ich
Was rOP ist konstant kommt aus der Summe:
M.ODER = rOP × (∑ F.ich)
Aber ∑ F.ich ist einfach die Nettokraft oder die resultierende Kraft F.R., Daher wird sofort der Schluss gezogen, dass:
M.ODER = rOP × F.R.
Beispiel
Der Satz von Varignon erleichtert die Berechnung des Kraftmoments F. In Bezug auf Punkt O in der in der Figur gezeigten Struktur wird berechnet, wenn die Kraft in ihre rechteckigen Komponenten zerlegt wird und das Moment von jedem von ihnen berechnet wird:
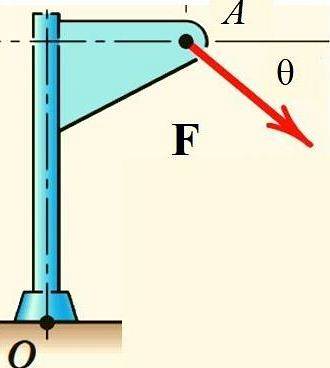
Anwendungen des Varignonschen Theorems
Wenn die resultierende Kraft eines Systems bekannt ist, kann der Satz von Varignon angewendet werden, um die Summe jedes der Momente zu ersetzen, die durch die Kräfte erzeugt werden, aus denen es besteht, bis zum Moment des Ergebnisses.
Wenn das System aus Kräften auf derselben Ebene besteht und der Punkt, für den das Moment berechnet werden soll, zu dieser Ebene gehört, ist das resultierende Moment senkrecht.
Wenn zum Beispiel alle Kräfte in der xy-Ebene liegen, ist das Moment in die z-Achse gerichtet und es bleibt nur, um seine Größe und seinen Sinn zu finden, wie dies im oben beschriebenen Beispiel der Fall ist.
In diesem Fall erlaubt uns der Satz von Varignon, das resultierende Moment des Systems durch die Summation zu berechnen. Dies ist sehr nützlich bei einem dreidimensionalen Kraftsystem, für das die Richtung des resultierenden Moments a priori nicht bekannt ist.
Um diese Übungen zu lösen, ist es zweckmäßig, Kräfte und Positionsvektoren in ihre rechteckigen Komponenten zu zerlegen und aus der Summe der Momente die Komponenten des Nettomoments zu bestimmen.
Übung gelöst
Berechnen Sie unter Verwendung des Varignonschen Theorems das Moment der Kraft F um den in der Abbildung gezeigten Punkt O, wenn die Größe von F 725 N beträgt.
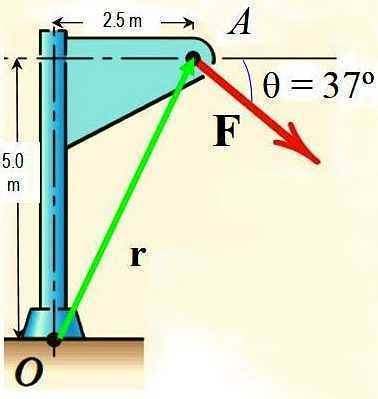
Lösung
Zerlegen Sie die Kraft, um den Satz von Varignon anzuwenden F. in zwei Komponenten, deren jeweilige Momente um O berechnet und addiert werden, um das resultierende Moment zu erhalten.
F.x = 725 N ∙ cos 37 º = 579,0 N.
F.Y. = - 725 N N ∙ sin 37 º = –436,3 N.
Ebenso der Positionsvektor r gerichtet von O nach A hat die Komponenten:
rx = 2,5 m
rY. = 5,0 m
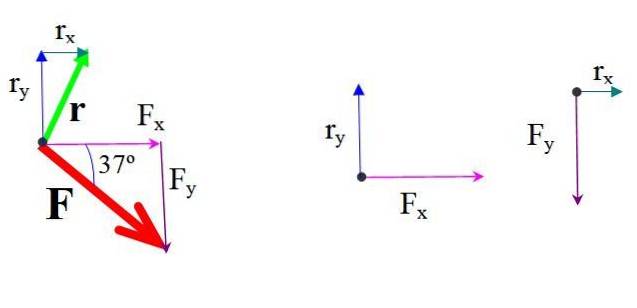
Das Moment jeder Komponente der Kraft um O wird durch Multiplizieren der Kraft und des senkrechten Abstands ermittelt.
Beide Kräfte neigen dazu, die Struktur in die gleiche Richtung zu drehen, in diesem Fall im Uhrzeigersinn, der willkürlich ein positives Vorzeichen zugewiesen wird:
M.Ochse = F.x∙ rY. ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m
M.Oy = F.Y.∙ rx ∙ sin (–90 °) = –436,3 N ∙ 2,5 m ∙ (–1) = 1090,8 N ∙ m
Der resultierende Moment über O ist:
M.ODER = M.Ochse + M.Oy = 3985,8 Nm senkrecht zur Ebene und im Uhrzeigersinn.
Verweise
- Bedford, 2000. A. Technische Mechanik: Statik. Addison Wesley.
- Beer, F. 2010. Statisch. McGraw Hill. 9 .. Auflage.
- Hibbeler, R. 1992. Mechanik für Ingenieure. 6 .. Auflage. CECSA.
- HK Engineering. Varignons Satz. Wiederhergestellt von: youtube.com.
- Wikipedia. Varignons Theorem (Mechanik). Wiederhergestellt von: en.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.