
Torricellis Theorem, woraus es besteht, Formeln und Übungen
Das Torricellis Theorem Das Torricelli-Prinzip besagt, dass die Geschwindigkeit der Flüssigkeit, die durch das Loch in der Wand eines Tanks oder Behälters austritt, mit der eines Objekts identisch ist, das aus einer Höhe frei fallen darf, die der der freien Oberfläche der Flüssigkeit entspricht bis zum Loch.
Der Satz ist in der folgenden Abbildung dargestellt:
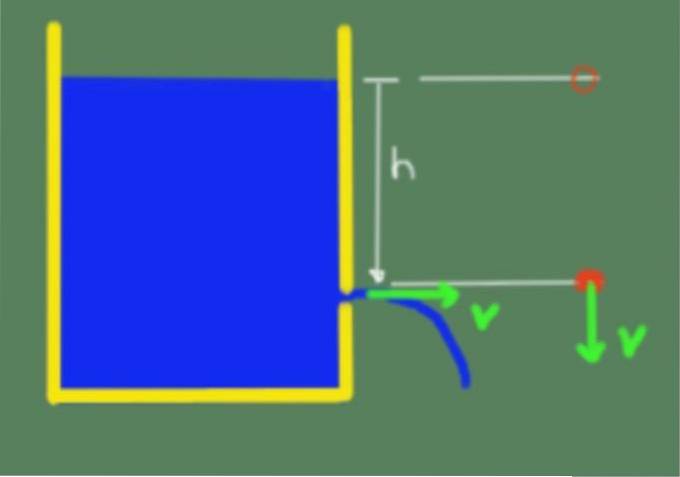
Aufgrund des Satzes von Torricelli können wir dann bestätigen, dass die Austrittsgeschwindigkeit der Flüssigkeit durch eine Öffnung, die sich in der Höhe h unter der freien Oberfläche der Flüssigkeit befindet, durch die folgende Formel gegeben ist:
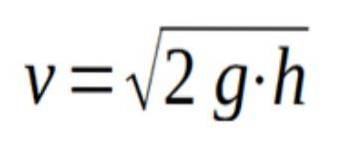
Dabei ist g die Erdbeschleunigung und h die Höhe vom Loch zur freien Oberfläche der Flüssigkeit.
Evangelista Torricelli war ein Physiker und Mathematiker, der 1608 in der italienischen Stadt Faenza geboren wurde. Torricelli wird die Erfindung des Quecksilberbarometers zugeschrieben, und als Anerkennung gibt es eine Druckeinheit namens „Torr“, die einem Millimeter Quecksilber (mm) entspricht Hg).
Artikelverzeichnis
- 1 Beweis des Satzes
- 1.1 Fallendes Objekt
- 1.2 Flüssigkeit tritt aus dem Loch aus
- 2 Gelöste Übungen
- 2.1 Übung 1
- 3 I) Das kleine Auslassrohr eines Wassertanks befindet sich 3 m unter der Wasseroberfläche. Berechnen Sie die Austrittsgeschwindigkeit des Wassers.
- 3.1 Übung 2
- 3.2 Übung 3
- 4 Referenzen
Beweis des Satzes
In Torricellis Theorem und in der Formel, die die Geschwindigkeit angibt, wird angenommen, dass die Viskositätsverluste vernachlässigbar sind, ebenso wie im freien Fall angenommen wird, dass die Reibung aufgrund der das fallende Objekt umgebenden Luft vernachlässigbar ist..
Die obige Annahme ist in den meisten Fällen vernünftig und beinhaltet auch die Erhaltung der mechanischen Energie.
Um den Satz zu beweisen, finden wir zunächst die Formel für die Geschwindigkeit eines Objekts, das mit einer Anfangsgeschwindigkeit von Null aus derselben Höhe wie die Flüssigkeitsoberfläche im Tank freigegeben wird..
Das Prinzip der Energieeinsparung wird angewendet, um die Geschwindigkeit des fallenden Objekts zu ermitteln, sobald es eine Höhe abgesunken ist h gleich dem vom Loch zur freien Oberfläche.
Da es keine Reibungsverluste gibt, gilt das Prinzip der Erhaltung der mechanischen Energie. Angenommen, das fallende Objekt hat die Masse m und die Höhe h wird vom Austrittsniveau der Flüssigkeit gemessen.
Fallendes Objekt
Wenn das Objekt aus einer Höhe freigesetzt wird, die der der freien Oberfläche der Flüssigkeit entspricht, ist seine Energie nur das Gravitationspotential, da seine Geschwindigkeit Null und daher seine kinetische Energie Null ist. Die potentielle Energie Ep ist gegeben durch:
Ep = m g h
Wenn es vor dem Loch vorbeigeht, ist seine Höhe Null, dann ist die potentielle Energie Null, so dass es nur kinetische Energie Ec hat, die gegeben ist durch:
Ec = ½ m vzwei
Da die Energie erhalten bleibt, ist Ep = Ec aus dem, was erhalten wird:
½ m vzwei = m g h
Nach Geschwindigkeit suchen v Die Torricelli-Formel wird dann erhalten:
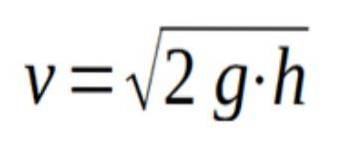
Flüssigkeit kommt aus dem Loch
Als nächstes finden wir die Austrittsgeschwindigkeit der Flüssigkeit durch das Loch, um zu zeigen, dass sie mit der übereinstimmt, die gerade für ein frei fallendes Objekt berechnet wurde.
Dafür stützen wir uns auf das Bernoulli-Prinzip, das nichts anderes ist als die Erhaltung der Energie, die auf Flüssigkeiten angewendet wird.
Bernoullis Prinzip lautet wie folgt:
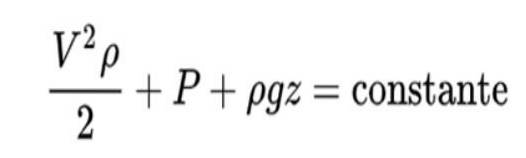
Die Interpretation dieser Formel lautet wie folgt:
- Der erste Term repräsentiert die kinetische Energie des Fluids pro Volumeneinheit
- Die zweite repräsentiert die Arbeit, die durch den Druck pro Einheitsquerschnittsfläche geleistet wird.
- Die dritte repräsentiert die potentielle Energie der Gravitation pro Volumeneinheit der Flüssigkeit..
Wenn wir von der Annahme ausgehen, dass es sich um ein ideales Fluid unter nicht turbulenten Bedingungen mit relativ geringen Geschwindigkeiten handelt, ist es wichtig zu bestätigen, dass die mechanische Energie pro Volumeneinheit in dem Fluid in allen Regionen oder Querschnitten des Fluids konstant ist gleich..
In dieser Formel V. ist die Geschwindigkeit der Flüssigkeit, ρ die Dichte der Flüssigkeit, P. Druck und z vertikale Position.
Die folgende Abbildung zeigt die Torricelli-Formel ausgehend vom Bernoulli-Prinzip.
Wir wenden die Bernoulli-Formel auf die freie Oberfläche der mit (1) bezeichneten Flüssigkeit und auf das mit (2) bezeichnete Austrittsloch an. Die Nullkopfhöhe wurde bündig mit dem Auslassloch gewählt.
Unter der Voraussetzung, dass der Querschnitt in (1) viel größer als in (2) ist, können wir dann annehmen, dass die Sinkgeschwindigkeit der Flüssigkeit in (1) praktisch vernachlässigbar ist.
Deshalb ist V.1= 0, der Druck, dem die Flüssigkeit in (1) ausgesetzt ist, ist Atmosphärendruck und die von der Öffnung gemessene Höhe ist h.
Für den Auslassabschnitt (2) nehmen wir an, dass die Auslassgeschwindigkeit v ist, der Druck, dem die Flüssigkeit am Auslass ausgesetzt ist, ebenfalls Atmosphärendruck ist und die Auslasshöhe Null ist.
Die den Abschnitten (1) und (2) entsprechenden Werte werden in der Bernoulli-Formel eingesetzt und gleich gesetzt. Die Gleichheit gilt, weil wir davon ausgehen, dass die Flüssigkeit ideal ist und keine viskosen Reibungsverluste auftreten. Sobald alle Begriffe vereinfacht wurden, wird die Geschwindigkeit am Austrittsloch erhalten.
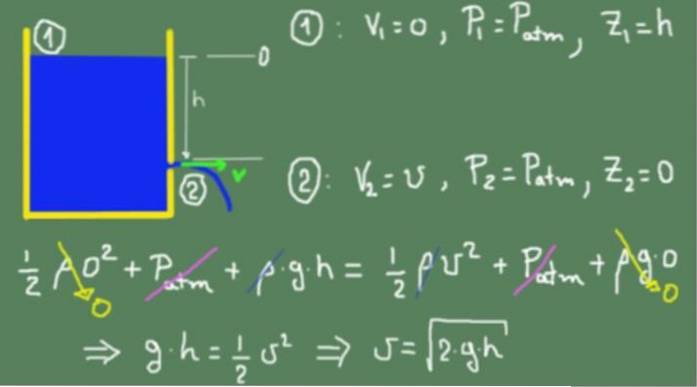
Das obige Feld zeigt, dass das erhaltene Ergebnis das gleiche ist wie das eines frei fallenden Objekts,
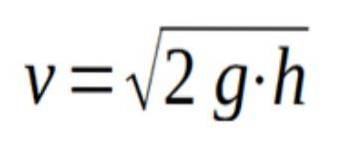
Gelöste Übungen
Übung 1
ich) Das kleine Auslassrohr eines Wassertanks befindet sich 3 m unter der Wasseroberfläche. Berechnen Sie die Austrittsgeschwindigkeit des Wassers.
Lösung:
Die folgende Abbildung zeigt, wie die Torricelli-Formel auf diesen Fall angewendet wird.
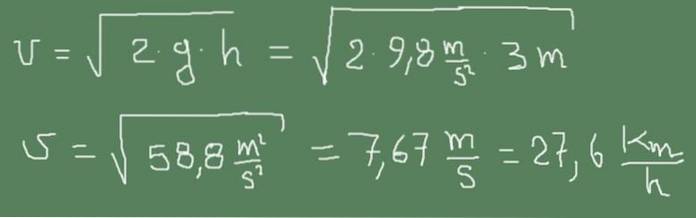
Übung 2
II) Berechnen Sie unter der Annahme, dass das Auslassrohr des Tanks aus der vorherigen Übung einen Durchmesser von 1 cm hat, den Wasserauslassfluss.
Lösung:
Die Durchflussrate ist das pro Zeiteinheit austretende Flüssigkeitsvolumen und wird einfach durch Multiplizieren der Fläche der Austrittsöffnung mit der Austrittsgeschwindigkeit berechnet.
Die folgende Abbildung zeigt die Details der Berechnung.

Übung 3
III) Bestimmen Sie, wie hoch die freie Wasseroberfläche in einem Behälter ist, wenn Sie wissen
dass in einem Loch im Boden des Behälters das Wasser mit 10 m / s austritt.
Lösung:
Selbst wenn sich das Loch am Boden des Behälters befindet, kann die Torricelli-Formel angewendet werden.
Die folgende Abbildung zeigt die Details der Berechnungen.

Verweise
- Wikipedia. Torricellis Theorem.
- Hewitt, P.. Konzeptionelle Physik. Fünfte Ausgabe.119.
- Jung, Hugh. 2016. Sears-Zemanskys Universitätsphysik mit moderner Physik. 14. Aufl. Pearson. 384.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.