
Thévenins Theorem, woraus es besteht, Anwendungen und Beispiele
Das Thévenins Satz gibt an, dass eine Schaltung mit den Klemmen A und B durch eine äquivalente ersetzt werden kann, die aus einer Quelle und einem Serienwiderstand besteht, deren Werte die gleiche Potentialdifferenz zwischen A und B und die gleiche Impedanz wie die ursprüngliche Schaltung ergeben.
Dieses Theorem wurde 1883 vom französischen Ingenieur Léon Charles Thévenin bekannt gemacht, aber es wird behauptet, dass es dreißig Jahre zuvor vom deutschen Physiker Hermann von Helmholtz ausgesprochen wurde.

Seine Nützlichkeit liegt in der Tatsache, dass sich das einfache Thévenin-Ersatzschaltbild selbst dann, wenn die ursprüngliche Schaltung komplex oder unbekannt ist, für die Zwecke einer Last oder Impedanz, die zwischen den Klemmen A und B angeordnet ist, genauso verhält wie die ursprüngliche.
Artikelverzeichnis
- 1 Wie berechnet man Schritt für Schritt die äquivalente Spannung??
- 1.1 - Experimentell
- 1.2 - Lösen der Schaltung
- 2 Anwendungen des Théveninschen Theorems (Teil I)
- 2.1 Beispiel 1a (schrittweise Berechnung der Ersatzspannung)
- 2.2 Beispiel 1b (Strom in der Last unter Verwendung des Thévenin-Äquivalents)
- 3 Beweis des Satzes von Thévenin
- 4 Anwendung des Théveninschen Theorems (Teil II)
- 4.1 Beispiel 2a (Thévenin-Äquivalentwiderstand)
- 4.2 Beispiel 2b
- 4.3 Beispiel 2c
- 5 Anwendung des Théveninschen Theorems (Teil III)
- 5.1 Beispiel 3
- 6 Referenzen
Wie berechnet man Schritt für Schritt die Ersatzspannung??
Die Spannungs- oder Potentialdifferenz des Ersatzschaltbilds kann auf folgende Weise erhalten werden:
- Experimentell
Erhalten der äquivalenten Thévenin-Spannung
Wenn sich ein Gerät oder eine Ausrüstung in einer „Black Box“ befindet, wird die Potentialdifferenz zwischen den Klemmen A und B mit einem Voltmeter oder einem Oszilloskop gemessen. Es ist sehr wichtig, dass keine Last oder Impedanz zwischen den Klemmen A und B liegt.
Ein Voltmeter oder ein Oszilloskop stellen keine Belastung für die Klemmen dar, da beide Geräte eine sehr große Impedanz haben (idealerweise unendlich) und es so wäre, als wären die Klemmen A und B ohne Last. Die auf diese Weise erhaltene Spannung oder Spannung ist die äquivalente Thévenin-Spannung.
Erhalten der äquivalenten Thévenin-Impedanz
Um die äquivalente Impedanz aus einer experimentellen Messung zu erhalten, wird ein bekannter Widerstand zwischen die Klemmen A und B gelegt und der Spannungsabfall oder das Spannungssignal mit einem Oszilloskop gemessen..
Aus dem Spannungsabfall des bekannten Widerstands zwischen den Klemmen kann der durch sie fließende Strom erhalten werden.
Das Produkt aus dem mit dem Ersatzwiderstand erhaltenen Strom plus dem im bekannten Widerstand gemessenen Spannungsabfall ist gleich der zuvor erhaltenen äquivalenten Thévenin-Spannung. Aus dieser Gleichheit wird die äquivalente Thévenin-Impedanz gelöscht.
- Schaltung lösen
Berechnung der Thévenin-Ersatzspannung
Zunächst wird jede Last oder Impedanz von den Klemmen A und B getrennt.
Wie die Schaltung bekannt ist, werden die Maschentheorie oder die Kirchhoffschen Gesetze angewendet, um die Spannung an den Klemmen zu ermitteln. Diese Spannung entspricht Thévenin.
Berechnung der Thévenin-Äquivalentimpedanz
Um die äquivalente Impedanz zu erhalten, fahren wir fort mit:
- Ersetzen Sie die Spannungsquellen des ursprünglichen Stromkreises durch Kurzschlüsse "Nullimpedanz" und die Stromquellen des ursprünglichen Stromkreises durch offene "unendliche Impedanz"..
- Dann wird die äquivalente Impedanz nach den Regeln der Serienimpedanzen und Parallelimpedanzen berechnet.
Anwendungen des Théveninschen Theorems (Teil I)
Wir werden den Satz von Thévenin anwenden, um einige Schaltkreise zu lösen. In diesem ersten Teil betrachten wir eine Schaltung, die nur Spannungsquellen und Widerstände aufweist.
Beispiel 1a (Berechnung der äquivalenten Spannung Schritt für Schritt)
Fig. 2 zeigt die Schaltung, die sich in einer Himmelsbox befindet, die zwei elektromotorische Kraftbatterien V1 bzw. V2 und Widerstände R1 und R2 aufweist. Die Schaltung hat Klemmen A und B, an die eine Last angeschlossen werden kann.
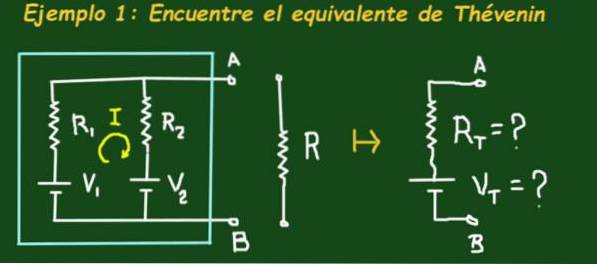
Das Ziel besteht darin, das Thévenin-Ersatzschaltbild zu finden, dh die Vt- und Rt-Werte des Ersatzschaltbilds zu bestimmen. Wenden Sie die folgenden Werte an: V1 = 4 V, V2 = 1 V, R1 = 3 Ω, R2 = 6 Ω und R = 1 Ω.
Schritt-für-Schritt Lösung
Schritt 1
Wir werden die Spannung an den Klemmen A und B bestimmen, wenn sie nicht belastet werden.
Schritt 2
Die zu lösende Schaltung besteht aus einem einzelnen Netz, durch das ein Strom I fließt, den wir im Uhrzeigersinn positiv aufgenommen haben.
Schritt 3
Wir gehen durch das Netz, beginnend mit der unteren linken Ecke. Der Pfad führt zu folgender Gleichung:
V1 - I * R1 - I * R2 - V2 = 0
Schritt 4
Wir lösen für den Maschenstrom I und erhalten:
I = (V1 - V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A.
Schritt 5
Mit dem Maschenstrom können wir die Spannungsdifferenz zwischen A und B bestimmen, die ist:
Vab = V1 - I * R1 = 4 V - ⅓ A * 3Ω = 3V
Das heißt, die Thevenin-Ersatzspannung beträgt: Vt = 3V.
Schritt 6 (Thévenin-Äquivalentwiderstand)
Wir berechnen nun den Thévenin-Ersatzwiderstand, für den und wie bereits erwähnt die Spannungsquellen durch ein Kabel ersetzt werden.
In diesem Fall haben wir nur zwei Widerstände parallel, daher ist der äquivalente Thévenin-Widerstand:
Rt = (R1 · R2) / (R1 + R2) = (3Ω · 6Ω) / (3Ω + 6Ω) = 2Ω
Beispiel 1b (Strom in der Last unter Verwendung des Thévenin-Äquivalents)
Schließen Sie als Last an die Klemmen A und B einen Widerstand R = 1 Ω an das Ersatzschaltbild an und ermitteln Sie den Strom, der durch die Last fließt.
Lösung
Wenn der Widerstand R mit dem Thevenin-Ersatzschaltbild verbunden ist, haben wir eine einfache Schaltung, die aus einer Quelle Vt und einem Widerstand Rt in Reihe mit dem Widerstand R besteht.
Wir werden Ic den Strom nennen, der durch die Last R fließt, so dass die Maschengleichung wie folgt aussieht:
Vt - Ic * Rt - Ic * R = 0
woraus folgt, dass Ic gegeben ist durch:
Ic = Vt / (Rt + R) = 3 V / (2Ω + 1Ω) = 1 A.
Beweis des Satzes von Thévenin
Um zu überprüfen, ob der Satz von Thévenin gilt, verbinden Sie R mit der ursprünglichen Schaltung und ermitteln Sie den durch R fließenden Strom, indem Sie das Maschengesetz auf die resultierende Schaltung anwenden.
Die resultierende Schaltung bleibt erhalten und ihre Maschengleichungen bleiben wie in der folgenden Abbildung gezeigt:
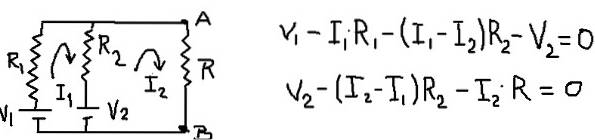
Durch Hinzufügen der Maschengleichungen ist es möglich, den Maschenstrom I1 als Funktion des Stroms I2 zu finden. Dann wird es in die zweite Maschengleichung eingesetzt und eine Gleichung mit I2 als einzigem Unbekannten belassen. Die folgende Tabelle zeigt die Operationen.
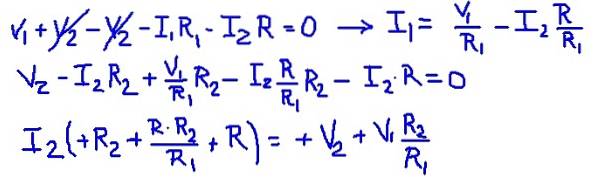
Dann werden die Werte des Widerstands und der Spannungen der Quellen ersetzt, wobei der numerische Wert des Maschenstroms I2 erhalten wird.

Der Maschenstrom I2 ist der Strom, der durch den Lastwiderstand R fließt, und der gefundene Wert von 1 A stimmt vollständig mit dem zuvor mit dem äquivalenten Thévenin-Schaltkreis gefundenen überein..
Anwendung des Théveninschen Theorems (Teil II)
In diesem zweiten Teil wird das Thévenin-Theorem in einer Schaltung angewendet, die Spannungsquellen, Stromquellen und Widerstände aufweist.
Beispiel 2a (Thévenin-Äquivalentwiderstand)
Das Ziel besteht darin, das Thévenin-Ersatzschaltbild zu bestimmen, das der Schaltung in der folgenden Abbildung entspricht. Wenn die Klemmen keinen Widerstand von 1 Ohm haben, wird der Widerstand platziert und der durch sie zirkulierende Strom bestimmt.
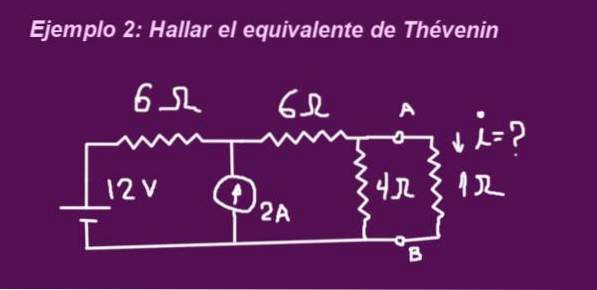
Lösung
Entfernen Sie den Lastwiderstand (in diesem Fall 1 Ohm), um den äquivalenten Widerstand zu ermitteln. Außerdem werden Spannungsquellen durch einen Kurzschluss und Stromquellen durch einen offenen Stromkreis ersetzt..
Auf diese Weise ist die Schaltung, für die der Ersatzwiderstand berechnet wird, die folgende:
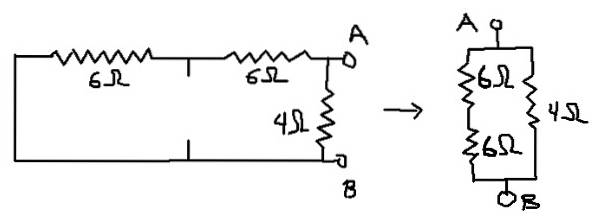
Rab = (12 Ω * 4 Ω) / (12 Ω + 4 Ω) = 3 Ω, was dem Thevenin-Äquivalentwiderstand (Rth) entspricht..
Beispiel 2b
Berechnen Sie die äquivalente Thévenin-Spannung.
Lösung
Um die Thévenin-Ersatzspannung zu berechnen, betrachten wir die folgende Schaltung, in der wir die Ströme in I1 und I2 in den in der folgenden Abbildung angegebenen Zweigen platzieren:
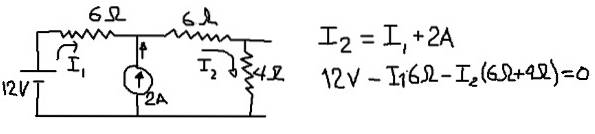
Die vorherige Abbildung zeigt die Gleichung der Stromknoten und die Spannungsgleichung beim Durchlaufen des externen Netzes. Aus der zweiten der Gleichungen wird der Strom I1 gelöscht:
I1 = 2 - I2 * (5/3)
Diese Gleichung wird in die Gleichung der Knoten eingesetzt:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A.
Dies bedeutet, dass der Spannungsabfall am 4-Ohm-Widerstand 6 Volt beträgt..
Kurz gesagt beträgt die Thévenin-Spannung Vth = 6 V..
Beispiel 2c
Finden der Thevenin-Ersatzschaltung und des Stroms im Lastwiderstand.
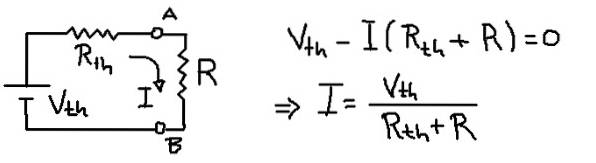
Lösung
Die vorige Abbildung zeigt das Thévenin-Ersatzschaltbild mit dem Lastwiderstand R. Aus der Spannungsgleichung im Netz wird der Strom I abgeleitet, der durch den Lastwiderstand R fließt.
I = Vth / (Rth + R) = 6 V / (3Ω + 1Ω) = 1,5 A.
Anwendung des Théveninschen Theorems (Teil III)
In diesem dritten Teil der Anwendung des Théveninschen Theorems wird ein Wechselstromkreis betrachtet, der eine Wechselspannungsquelle, einen Kondensator, eine Induktivität und einen Widerstand enthält..
Beispiel 3
Ziel ist es, den Thévenin Circuit zu finden, der dem folgenden Circuit entspricht:
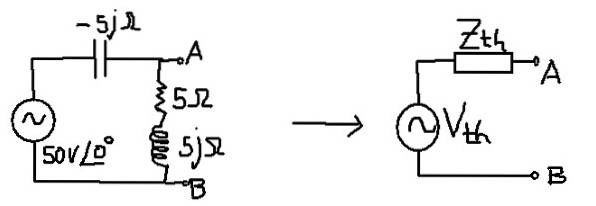
Lösung
Die äquivalente Impedanz entspricht der des Kondensators parallel zur Reihenschaltung von Widerstand und Induktivität.
Die Umkehrung der äquivalenten Impedanz ist gegeben durch:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
Und die äquivalente Impedanz ist dann:
Zeq = (1 - 3 j) Ohm
Der komplexe Strom I kann aus der Netzgleichung abgeleitet werden:
50 V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Nun wird der Spannungsabfall im Widerstand plus die Induktivität berechnet, dh die Spannung Vab, die der äquivalenten Thévenin-Spannung entspricht:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Mit anderen Worten, die äquivalente Spannung hat den gleichen Spitzenwert wie die ursprüngliche Quelle, ist jedoch um 45 Grad phasenverschoben: Vth = 50 V ~ 45 °
Verweise
- Elektronik-Tutorials, Thevenins Theorem. Wiederhergestellt von: electronic-tutorials.ws
- Fragen und Antworten zur Netzwerktheorie. Thevenins Theorem. Wiederhergestellt von: sanfoundry.com
- Thevenins Theorem. Schritt für Schritt. Wiederhergestellt von: electrictechnology.org
- Thevenins Theorem. Beispiel Schritt für Schritt gelöst. Wiederhergestellt von: electricicalsimple.blogspot.com
- Workshop zu Thevenins und Nortons Theoremen. Wiederhergestellt von: web.iit.edu
- Wikipedia. Thévenins Satz. Wiederhergestellt von: wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.