Euklids Theorem Beweis, Anwendung und Übungen

Das Satz von Euklid demonstriert die Eigenschaften eines rechtwinkligen Dreiecks, indem eine Linie gezeichnet wird, die es in zwei neue rechtwinklige Dreiecke unterteilt, die einander ähnlich sind und wiederum dem ursprünglichen Dreieck ähnlich sind; dann gibt es ein Verhältnis der Verhältnismäßigkeit.

Euklid war einer der größten Mathematiker und Geometriker der Antike, der mehrere Beweise für wichtige Theoreme lieferte. Einer der wichtigsten ist derjenige, der seinen Namen trägt und eine breite Anwendung gefunden hat.

Dies war der Fall, weil durch diesen Satz auf einfache Weise die geometrischen Beziehungen erklärt werden, die im rechtwinkligen Dreieck existieren, wobei die Beine davon mit ihren Projektionen in der Hypotenuse zusammenhängen..

Artikelverzeichnis

• 1 Formeln und Beweis
  • 1.1 Höhensatz
  • 1.2 Beinsatz
• 2 Beziehung zwischen Euklids Theoremen
• 3 Gelöste Übungen
  • 3.1 Beispiel 1
  • 3.2 Beispiel 2
• 4 Referenzen

Formeln und Demonstration

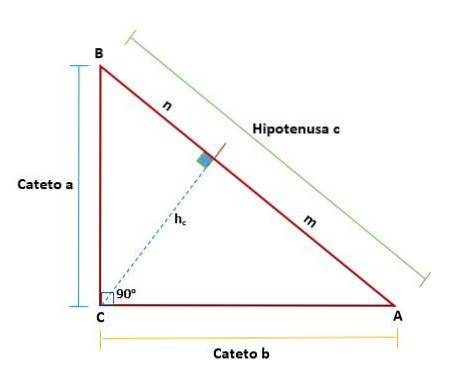
Der Satz von Euklid schlägt vor, dass in jedem rechtwinkligen Dreieck beim Zeichnen einer Linie - die die Höhe darstellt, die dem Scheitelpunkt des rechten Winkels in Bezug auf die Hypotenuse entspricht - zwei rechtwinklige Dreiecke aus dem Original gebildet werden.

Diese Dreiecke sind einander ähnlich und ähneln auch dem ursprünglichen Dreieck, was bedeutet, dass ihre ähnlichen Seiten proportional zueinander sind:

Die Winkel der drei Dreiecke sind kongruent; Das heißt, wenn sie um 180 Grad um ihren Scheitelpunkt gedreht werden, fällt ein Winkel mit dem anderen zusammen. Dies impliziert, dass sie alle gleich sein werden.

Auf diese Weise kann die Ähnlichkeit, die zwischen den drei Dreiecken besteht, auch durch die Gleichheit ihrer Winkel überprüft werden. Aus der Ähnlichkeit von Dreiecken bestimmt Euklid die Proportionen dieser aus zwei Theoremen:

- Höhensatz.

- Beinsatz.

Dieser Satz hat eine breite Anwendung. In der Antike wurde es zur Berechnung von Höhen oder Entfernungen verwendet, was einen großen Fortschritt für die Trigonometrie darstellt.

Es wird derzeit in verschiedenen Bereichen angewendet, die auf Mathematik basieren, wie Ingenieurwesen, Physik, Chemie und Astronomie, unter vielen anderen Bereichen..

Höhensatz

In diesem Satz wird festgestellt, dass in jedem rechtwinkligen Dreieck die Höhe, die aus dem rechten Winkel in Bezug auf die Hypotenuse gezogen wird, das geometrische proportionale Mittel (das Quadrat der Höhe) zwischen den Projektionen der Beine ist, das es auf der Hypotenuse bestimmt.

Das heißt, das Quadrat der Höhe entspricht der Multiplikation der projizierten Beine, die die Hypotenuse bilden:

h_c^zwei = m _{* *} n

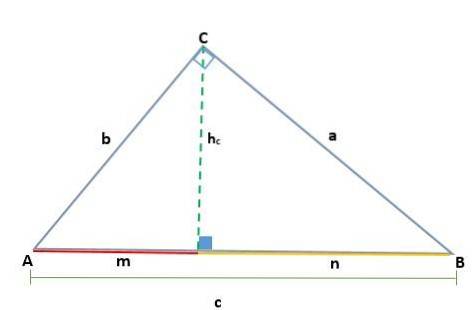
Demonstration

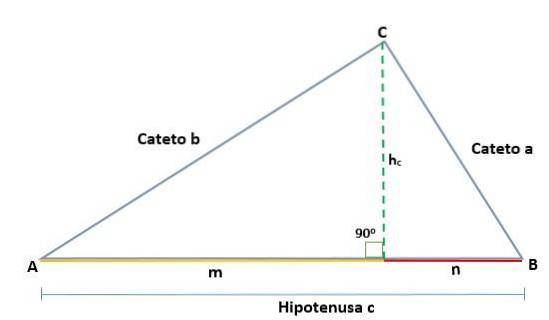
Wenn ein Dreieck ABC gegeben ist, das genau am Scheitelpunkt C liegt, erzeugt das Zeichnen der Höhe zwei ähnliche rechtwinklige Dreiecke, ADC und BCD; Daher sind ihre entsprechenden Seiten proportional:

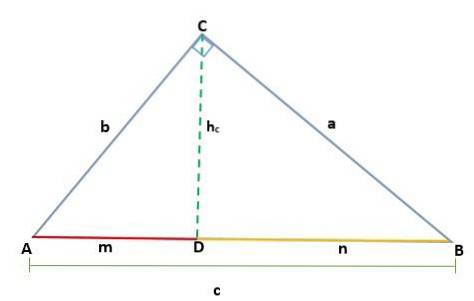
So, dass die Höhe h_c was dem Segment CD entspricht, entspricht der Hypotenuse AB = c, also haben wir:

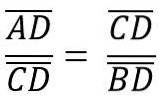
Dies entspricht wiederum:

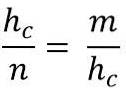
Auflösen nach der Hypotenuse (h_c), um die beiden Mitglieder der Gleichheit zu multiplizieren, müssen wir:

h_{c *} h_{c =} m _{* *} n

h_c^zwei = m _{* *} n

Somit ist der Wert der Hypotenuse gegeben durch:

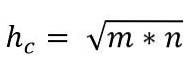
Beinsatz

In diesem Theorem wird festgelegt, dass in jedem rechtwinkligen Dreieck das Maß jedes Beins das geometrische proportionale Mittel (das Quadrat jedes Beins) zwischen dem Maß der Hypotenuse (vollständig) und der Projektion jedes einzelnen darauf ist:

b^zwei = c _{* *} m

zu^zwei = c_{* *} n

Demonstration

Wenn ein Dreieck ABC gegeben ist, das genau am Scheitelpunkt C liegt, so dass seine Hypotenuse c ist, werden beim Auftragen der Höhe (h) die Projektionen der Beine a und b bestimmt, die die Segmente m bzw. n sind. und die auf Hypotenuse liegen.

Wir haben also, dass die auf dem rechtwinkligen Dreieck ABC gezeichnete Höhe zwei ähnliche rechtwinklige Dreiecke erzeugt, ADC und BCD, so dass die entsprechenden Seiten wie folgt proportional sind:

DB = n, das ist die Projektion des Bein-CB auf die Hypotenuse.

AD = m, das ist die Projektion des Bein-AC auf die Hypotenuse.

Dann wird die Hypotenuse c durch die Summe der Beine ihrer Projektionen bestimmt:

c = m + n

Aufgrund der Ähnlichkeit der Dreiecke ADC und BCD haben wir:

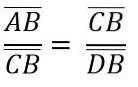
Das Obige ist dasselbe wie:

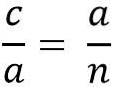
Wenn wir nach Bein „a“ suchen, um die beiden Mitglieder der Gleichheit zu multiplizieren, haben wir:

zu _{* *} a = c _{* *} n

zu^zwei = c _{* *} n

Somit ist der Wert von Bein "a" gegeben durch:

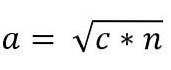
Auf die gleiche Weise haben wir aufgrund der Ähnlichkeit der Dreiecke ACB und ADC:

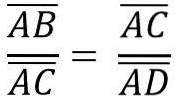
Das Obige ist gleich:

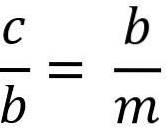
Wenn wir nach Bein "b" suchen, um die beiden Mitglieder der Gleichheit zu multiplizieren, haben wir:

b _{* *} b = c _{* *} m

b^zwei = c _{* *} m

Somit ist der Wert von Bein "b" gegeben durch:

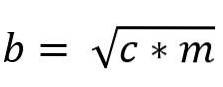
Beziehung zwischen Euklids Theoremen

Die Sätze in Bezug auf die Höhe und die Beine sind miteinander verbunden, da das Maß für beide in Bezug auf die Hypotenuse des rechtwinkligen Dreiecks gemacht wird.

Durch die Beziehung der Sätze von Euklid kann auch der Wert der Höhe gefunden werden; Dies ist möglich, indem die Werte von m und n aus dem Beinsatz gelöst werden und sie im Höhensatz ersetzt werden. Auf diese Weise ist es zufriedenstellend, dass die Höhe gleich der Multiplikation der Beine ist, geteilt durch die Hypotenuse:

b^zwei = c _{* *} m

m = b^zwei ÷ c

zu^zwei = c _{* *} n

n = a^zwei ÷ c

Im Höhensatz ersetzen wir m und n:

h_c^zwei = m _{* *} n

h_c^zwei = (b^zwei ÷ c) _{* *} (zu^zwei ÷ c)

h_c = (b^zwei _{* *} zu^zwei) ÷ c

Gelöste Übungen

Beispiel 1

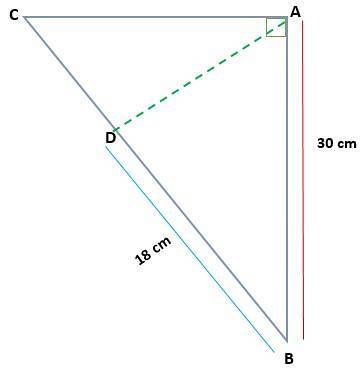
Bestimmen Sie anhand des Dreiecks ABC direkt bei A das Maß für AC und AD, wenn AB = 30 cm und BD = 18 cm

Lösung

In diesem Fall haben wir die Maße eines der projizierten Beine (BD) und eines der Beine des ursprünglichen Dreiecks (AB). Auf diese Weise kann der Beinsatz angewendet werden, um den Wert von Bein BC zu ermitteln.

AB^zwei = BD _{* *} BC

(30)^zwei = 18 _{* *} BC

900 = 18 _{* *} BC

BC = 900 ÷ 18

BC = 50 cm

Der Wert der Bein-CD kann mit dem Wissen ermittelt werden, dass BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Jetzt ist es möglich, den Wert von Bein AC zu bestimmen, indem der Beinsatz erneut angewendet wird:

AC^zwei = CD _{* *} BD

AC^zwei = 32 _{* *} fünfzig

AC^zwei = 160

AC = √1600 = 40 cm

Um den Wert der Höhe (AD) zu bestimmen, wird der Höhensatz angewendet, da die Werte der projizierten Beine CD und BD bekannt sind:

ANZEIGE^zwei = 32 _{* *} 18

ANZEIGE^zwei = 576

AD = √576

AD = 24 cm

Beispiel 2

Bestimmen Sie den Wert der Höhe (h) eines Dreiecks MNL direkt in N und kennen Sie die Maße der Segmente:

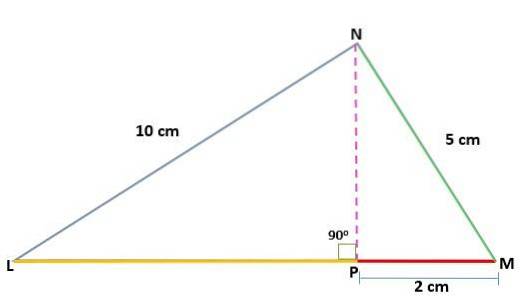
NL = 10 cm

MN = 5 cm

PM = 2 cm

Lösung

Wir haben das Maß eines der auf die Hypotenuse (PM) projizierten Beine sowie das Maß der Beine des ursprünglichen Dreiecks. Auf diese Weise kann der Beinsatz angewendet werden, um den Wert des anderen projizierten Beines (LN) zu ermitteln:

NL^zwei = PM _{* *} LM

(10)^zwei = 5 _{* *} LM

100 = 5 _{* *} LM

PL = 100 ÷ 5 = 20

Da der Wert der Beine und der Hypotenuse bereits bekannt ist, kann durch die Beziehung der Sätze der Höhe und der Beine der Wert der Höhe bestimmt werden:

NL = 10

MN = 5

LM = 20

h = (b^zwei _{* *} zu^zwei) ÷ c.

h = (10^zwei _{* *} 5^zwei)  ÷ (zwanzig)

h = (100 _{* *} 25) ÷ (zwanzig)

h = 2500 ÷ zwanzig

h = 125 cm.

Verweise

1. Braun, E. (2011). Chaos, Fraktale und seltsame Dinge. Fonds für Wirtschaftskultur.
2. Cabrera, V. M. (1974). Moderne Mathematik, Band 3.
3. Daniel Hernandez, D. P. (2014). 3. Jahr Mathe. Caracas: Santillana.
4. Encyclopaedia Britannica, ich. (1995). Hispanic Encyclopedia: Macropedia. Encyclopedia Britannica Publishers.
5. Euclid, R. P. (1886). Euklids Elemente der Geometrie.
6. Guardeño, A. J. (2000). Das Erbe der Mathematik: von Euklid bis Newton, die Genies durch ihre Bücher. Sevilla Universität.