
Erklärung des zweiten Gleichgewichtszustands, Beispiele, Übungen
Das zweite Gleichgewichtsbedingung legt fest, dass die Summe der Drehmomente oder Momente, die von allen auf einen Körper einwirkenden Kräften erzeugt werden, unabhängig davon, welcher Punkt berechnet wird, aufgehoben werden muss, damit sich der Körper im statischen oder dynamischen Gleichgewicht befindet.
Bezeichnet das Drehmoment oder den Moment der Kraft durch den griechischen Buchstaben τ, mathematisch wird es so ausgedrückt:
∑ τ = 0

Der fette Buchstabe gibt die Vektornatur des Moments an, die in Bezug auf jeden als Drehpunkt gewählten Punkt aufgehoben werden muss. Auf diese Weise wird durch Aufheben des Nettodrehmoments sichergestellt, dass sich das Objekt nicht zu drehen beginnt oder umkippt..
Wenn sich das Objekt jedoch bereits zuvor gedreht hat und das Nettodrehmoment plötzlich verschwindet, wird die Drehung fortgesetzt, jedoch mit konstanter Winkelgeschwindigkeit.
Die zweite Gleichgewichtsbedingung wird in Verbindung mit der ersten Bedingung verwendet, die besagt, dass die Summe der auf einen Körper einwirkenden Kräfte Null sein muss, damit er sich nicht übersetzt, oder wenn dies der Fall ist, mit gleichmäßiger geradliniger Bewegung:
∑ F. = 0
Beide Bedingungen gelten für ausgedehnte Körper, deren Abmessungen messbar sind. Wenn angenommen wird, dass ein Objekt ein Teilchen ist, macht es keinen Sinn, von Rotationen zu sprechen, und die erste Bedingung reicht aus, um ein Gleichgewicht zu gewährleisten.
Beispiele
Die zweite Gleichgewichtsbedingung zeigt sich in unzähligen Situationen:
Wie du die Leiter hochkletterst
Wenn wir eine Leiter auf dem Boden und an der Wand abstützen, benötigen wir insbesondere auf dem Boden genügend Reibung, um sicherzustellen, dass die Leiter nicht verrutscht. Wenn wir versuchen, auf eine Leiter zu klettern, die auf einem öligen, nassen oder rutschigen Boden steht, ist es nicht schwer zu erwarten, dass wir fallen werden.
Um die Leiter sicher benutzen zu können, muss sie beim Klettern und auf der gewünschten Sprosse im statischen Gleichgewicht sein.
Einen Schrank bewegen
Wenn Sie ein hohes Möbelstück wie einen Schrank oder ein Möbelstück bewegen möchten, dessen Höhe größer als seine Breite ist, ist es praktisch, auf einen niedrigen Punkt zu drücken, um ein Umkippen zu vermeiden. Auf diese Weise ist es wahrscheinlicher, dass das Möbel rutschen statt sich zu drehen und legen sich hin.
Unter solchen Umständen sind die Möbel nicht unbedingt im Gleichgewicht, da sie sich schnell bewegen könnten, aber zumindest nicht umkippen würden.
Balkone
Die Balkone, die aus den Gebäuden herausragen, sollten so gebaut werden, dass sie auch bei vielen Personen nicht umkippen und einstürzen.
Dielektrika in externen elektrischen Feldern
Durch Platzieren eines dielektrischen Materials in einem externen elektrischen Feld bewegen sich die Moleküle und drehen sich, bis sie eine Gleichgewichtsposition einnehmen, wodurch ein elektrisches Feld innerhalb des Materials erzeugt wird..
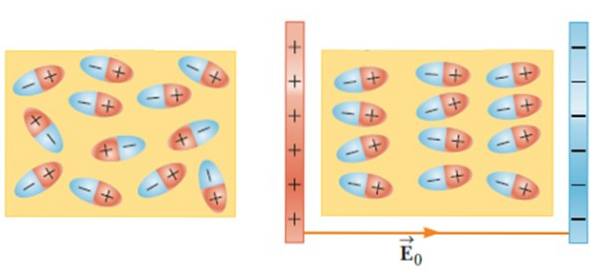
Dieser Effekt erhöht die Kapazität eines Kondensators, wenn ein Material wie Glas, Gummi, Papier oder Öl zwischen seine Rahmen eingefügt wird..
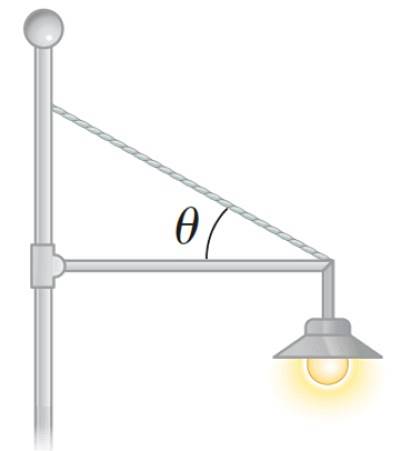
Schilder und Lampen
Es ist üblich, dass viele Einheimische Hinweise an die Wand des Gebäudes hängen, damit sie für Passanten sichtbar sind.
Das Poster wird von einer Stange und einem Kabel gehalten, die beide mit Klammern an der Wand befestigt sind. Die verschiedenen Kräfte, die wirken, müssen sicherstellen, dass das Plakat nicht fällt, wofür die beiden Gleichgewichtsbedingungen ins Spiel kommen.
Ein Reflektor kann auf diese Weise auch in einem Park platziert werden, wie in der folgenden Abbildung dargestellt:
Wie berechnet man das Nettodrehmoment oder das Nettomoment einer Kraft??
Das Drehmoment oder Moment einer Kraft, bezeichnet mit τ oder M. In einigen Texten wird es immer in Bezug auf einen Punkt berechnet, an dem die Rotationsachse verläuft.
Es ist definiert als das Vektorprodukt zwischen dem Positionsvektor r, das ist von dieser Achse zum Angriffspunkt der Kraft und der Kraft gerichtet F.::
τ = r × F.
Als Vektor ist es notwendig, das Drehmoment durch Angabe seiner Größe, Richtung und seines Sinns auszudrücken. Die Größe ist gegeben durch:
τ = rF.sen θ
Rechte Regel für Vektorprodukt
Wenn das Problem in der Ebene liegt, ist die Richtung des Drehmoments senkrecht zum Papier oder Bildschirm, und die Richtung wird durch die Rechtsregel bestimmt, in die der Zeigefinger zeigt r, Mittelfinger in Richtung F. und der Daumen zeigt in oder aus dem Papier.
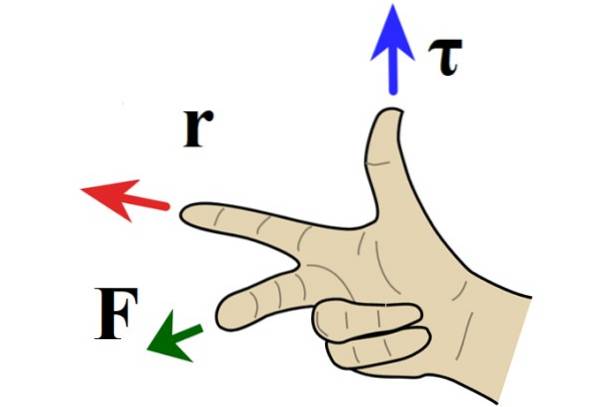
Wenn das Drehmoment aus dem Papier heraus zeigt, ist die Drehung gegen den Uhrzeigersinn und wird gemäß Konvention mit einem positiven Vorzeichen versehen. Wenn stattdessen das Drehmoment auf die Innenseite der Klinge gerichtet ist, ist die Drehung im Uhrzeigersinn und negativ..
Um das Nettodrehmoment zu ermitteln, wird ein geeigneter Punkt für die Berechnung ausgewählt, an dem möglicherweise die meisten Kräfte wirken. In diesem Fall ist das Moment dieser Kräfte Null, da es einen Positionsvektor hat r der Größe 0.
Sie können einen beliebigen Punkt auswählen, der genügend Informationen bietet, um das Unbekannte zu lösen, bei dem das Problem gelöst werden soll. Lassen Sie es uns unten genauer sehen.
Übung gelöst
Der Reflektor in der folgenden Abbildung hat eine Masse von 20 kg und wird von einer dünnen horizontalen Stange mit vernachlässigbarer Masse und Länge L getragen, die an einer Stange angelenkt ist. Das ebenfalls leichte Kabel, das zur Unterstützung des Reflektors beiträgt, bildet mit der Stange einen Winkel θ = 30º. Berechnung:
a) Die Spannung im Kabel
b) Die Größe der Kraft F, die der Pfosten durch das Scharnier auf die Stange ausübt.
Lösung
Wir werden die erste Gleichgewichtsbedingung ∑ anwenden F. = 0 zu den im Diagramm gezeigten Kräften:
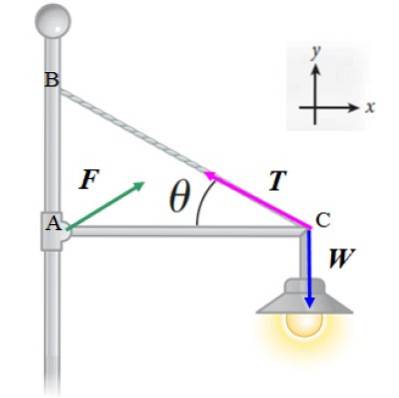
F. + T. + W = 0
Beachten Sie, dass die Größe und Richtung von F. sind noch zu bestimmen, aber wir nehmen an, dass es zwei Komponenten hat: F.x und F.Y.. Auf diese Weise erhalten wir zwei Gleichungen:
F.x -T. cos θ = 0
F.Y. - W + T⋅ sin θ = 0
Wenden wir nun die zweite Gleichgewichtsbedingung an und wählen Punkt A, da wir die Größe von nicht kennen F. noch das von T.. Durch Auswahl dieses Punktes wird der Vektor rZU ist null, daher der Moment von F. ist null und die Größe von F. erscheint nicht in der Gleichung:
-W⋅L + T⋅sen θ⋅L = 0
Deshalb:
T.sen θ.L = W.L.
T = W / sin & thgr; = (20 kg × 9,8 m / szwei) / Sin 30º = 392 N.
Wenn wir die Größe von T kennen, können wir nach der Komponente F lösenx::
F.x = T⋅ cos θ = 392 cos 30º N = 339. 5 N.
Und dann Komponente F.Y.::
F.Y. = W - T⋅ sin θ = (20 kg × 9,8 m / szwei) - 392⋅sin 30º = 0
Dann können wir ausdrücken F. So:
F = 339,5 N. x
Es ist daher eine horizontale Kraft. Dies liegt daran, dass wir davon ausgegangen sind, dass die Stange ein vernachlässigbares Gewicht hat.
Wenn Punkt C gewählt worden wäre, um das resultierende Moment zu berechnen, die Vektoren rT. Y. rW. sind daher null:
M = F.undL = 0
Es wird gefolgert, dass F.Y. = 0. Auf diese Weise:
- W + T⋅ sin θ = 0
T = W / sin & thgr;
Dies ist das gleiche Ergebnis, das anfänglich erzielt wurde, wenn Punkt A als Ort ausgewählt wurde, an dem die Rotationsachse verläuft.
Themen von Interesse
Gleichgewichtsbedingungen.
Erster Gleichgewichtszustand.
Verweise
- Bedford, 2000. A. Technische Mechanik: Statik. Addison Wesley.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 4. Partikelsysteme. Herausgegeben von Douglas Figueroa (USB).
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.