Das mathematische Beziehung ist die Verbindung, die zwischen den Elementen einer Teilmenge in Bezug auf das Produkt zweier Mengen besteht. EIN Funktion beinhaltet die mathematische Operation, um den Wert einer abhängigen Variablen basierend auf dem Wert einer unabhängigen Variablen zu bestimmen. Jede Funktion ist eine Beziehung, aber nicht jede Beziehung ist eine Funktion.
| Beziehung | Funktion | |
|---|---|---|
| Definition | Teilmenge geordneter Paare, die dem kartesischen Produkt zweier Mengen entsprechen. | Mathematische Operation, die mit der Variablen ausgeführt werden soll x um die Variable zu erhalten Y.. |
| Notation | x R. Y.;; x es ist verwandt mit Y.. | Y.= ƒ (x); Y. ist eine Funktion von x. |
| Eigenschaften |
|
|
| Beispiele |
|
|
Es wird die binäre Beziehung einer Menge A in einer Menge B oder die Beziehung zwischen Elementen von A und B zu jeder Teilmenge C des kartesischen Produkts A x B genannt.
Das heißt, wenn die Menge A aus den Elementen 1, 2 und 3 besteht und die Menge B aus den Elementen 4 und 5 besteht, ist das kartesische Produkt von A x B die geordneten Paare:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Die Teilmenge C = (2,4), (3,5) ist eine Beziehung von A und B, da sie sich aus den geordneten Paaren (2,4) und (3, 5) zusammensetzt, dem Ergebnis des Kartesischen Produkt von A x B..
"Sei A und B zwei beliebige nicht leere Mengen, sei A x B die Produktmenge von beiden, dh: A x B wird durch die geordneten Paare (x, y) so gebildet, dass x ist das Element von A und Y. es ist für B. Wenn eine Teilmenge C in A x B definiert ist, wird eine binäre Beziehung in A und B automatisch wie folgt bestimmt:
x R. Y. genau dann, wenn (x, y) ∈ C.
(die Notation x R. Y. Meint "x es ist verwandt mit Y.").
Wir werden Set A nennen Startsatz und wir werden Set B nennen Ankunft eingestellt.
Das Beziehungsdomäne sind die Elemente, aus denen der Startsatz besteht, während die Verhältnisbereich sind die Elemente des Ankunftssatzes.
einstellen ZU von x Elemente von Männern in einer Bevölkerung und B ist die Menge von Y. Elemente von Frauen aus der gleichen Bevölkerung. Eine Beziehung wird hergestellt, wenn "x ist verheiratet mit Y."".
Wenn wir über eine mathematische Funktion einer Menge A in einer Menge B sprechen, beziehen wir uns auf eine Regel oder einen Mechanismus, der die Elemente der Menge A mit einem Element der Menge B in Beziehung setzt.
"Sean x Y. Y. zwei reelle Variablen, heißt es dann y ist eine Funktion von x Ja zu jedem Wert, den ich nehme x entspricht einem Wert von Y..""
Die unabhängige Variable ist x während Y. ist die abhängige Variable oder Funktion:
y = ƒ (x)
Das Set, in dem die x es wird genannt Domäne der Funktion (Original) und die Variation von Y. Funktionsbereich (Bild).
Die Menge der Paare (x, Y.) so dass Y.= ƒ (x) wird genannt Funktionsgraph;; Wenn sie in kartesischen Achsen dargestellt werden, wird eine Familie von Punkten erhalten, die als bezeichnet wird Funktionsgraph.
In der Mathematik erhalten wir viele Beispiele für Funktionen. Hier sind Beispiele für Flaggschifffunktionen.
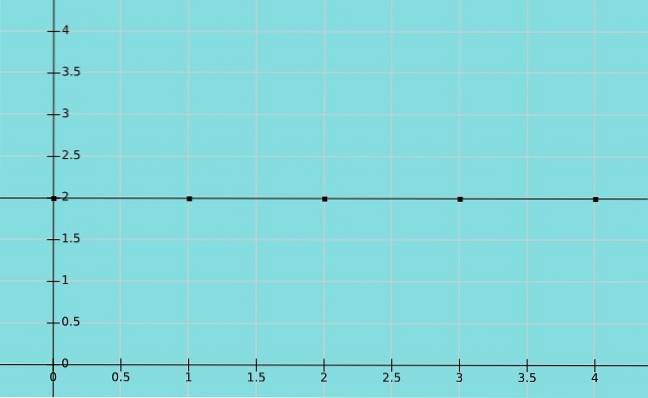
Eine Funktion heißt konstant, wenn das Element der Menge B, das der Menge A entspricht, dasselbe ist. In diesem Fall entsprechen alle Werte von x dem gleichen Wert von y. Somit ist die Domäne die reellen Zahlen, während der Bereich ein konstanter Wert ist.
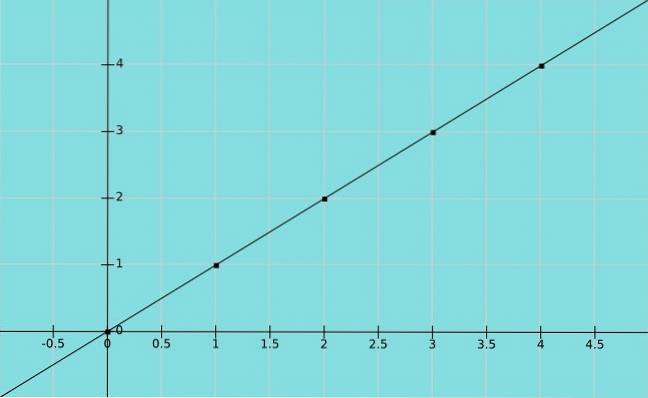
Nehmen wir an x ist eine Variable und das Y. nimmt den gleichen Wert an wie x. Wir haben dann eine Identitätsfunktion y = x, wo die Paarex, y) in der Grafik sind (1,1), (2,2), (3,3) und so weiter.
Eine Polynomfunktion erfüllt die Form y = anxn+zun-1+xn-1+… + A.zweixzwei+zu1x + a0. Die obige Grafik zeigt die Funktion ƒ (x) = xzwei+x-2.
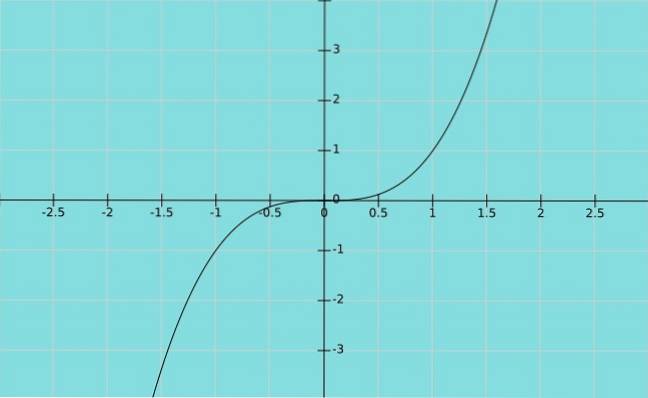
Nehmen wir nun an, dass die abhängige Variable Y. entspricht der unabhängigen Variablen x zum Würfel erhoben. Wir haben die Funktion y = x3, deren Grafik ist unten gezeigt:
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.