EIN empirische Regel Es ist das Ergebnis praktischer Erfahrung und realer Beobachtung. Zum Beispiel ist es möglich zu wissen, welche Vogelarten zu bestimmten Jahreszeiten an bestimmten Orten beobachtet werden können, und aus dieser Beobachtung kann eine "Regel" festgelegt werden, die die Lebenszyklen dieser Vögel beschreibt.
In der Statistik bezieht sich die empirische Regel auf die Art und Weise, in der Beobachtungen um einen zentralen Wert, den Mittelwert oder Durchschnitt, in Einheiten der Standardabweichung gruppiert werden..
Angenommen, Sie haben eine Gruppe von Personen mit einer durchschnittlichen Körpergröße von 1,62 Metern und einer Standardabweichung von 0,25 Metern. Mit der empirischen Regel können Sie beispielsweise definieren, wie viele Personen sich in einem Intervall des Mittelwerts plus oder minus eins befinden würden Standardabweichung?
Gemäß der Regel sind 68% der Daten mehr oder weniger eine Standardabweichung vom Mittelwert, dh 68% der Personen in der Gruppe haben eine Körpergröße zwischen 1,37 (1,62-0,25) und 1,87 (1,62 + 0,25). Meter.
Artikelverzeichnis
Die empirische Regel ist eine Verallgemeinerung des Tchebyshev-Theorems und der Normalverteilung.
Der Satz von Tchebyshev besagt: Für einen Wert von k> 1 ist die Wahrscheinlichkeit, dass eine Zufallsvariable zwischen dem Mittelwert minus k mal der Standardabweichung und dem Mittelwert plus k mal liegt, größer oder gleich (1 - 1) / kzwei).
Der Vorteil dieses Theorems besteht darin, dass es für diskrete oder kontinuierliche Zufallsvariablen mit beliebiger Wahrscheinlichkeitsverteilung gilt, die daraus definierte Regel jedoch nicht immer sehr genau ist, da sie von der Symmetrie der Verteilung abhängt. Je verzerrter die Verteilung der Zufallsvariablen ist, desto weniger ist ihr Verhalten an die Regel angepasst.
Die aus diesem Satz definierte empirische Regel lautet:
Wenn k = √2 ist, wird gesagt, dass 50% der Daten im Intervall liegen: [µ - √2 s, µ + √2 s]
Wenn k = 2 ist, wird gesagt, dass 75% der Daten im Intervall liegen: [µ - 2 s, µ + 2 s]
Wenn k = 3 ist, wird gesagt, dass 89% der Daten im Intervall liegen: [µ - 3 s, µ + 3 s]
Die Normalverteilung oder Gaußsche Glocke ermöglicht es, die empirische Regel oder Regel 68 - 95 - 99.7 festzulegen.
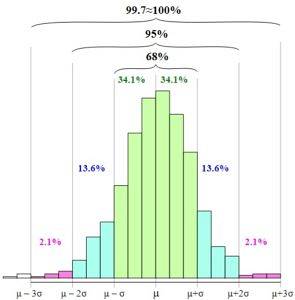
Die Regel basiert auf den Wahrscheinlichkeiten des Auftretens einer Zufallsvariablen in Intervallen zwischen dem Mittelwert minus einer, zwei oder drei Standardabweichungen und dem Mittelwert plus einer, zwei oder drei Standardabweichungen..
Die empirische Regel definiert folgende Intervalle:
68,27% der Daten liegen im Intervall: [µ - s, µ + s]
95,45% der Daten liegen im Intervall: [µ - 2s, µ + 2s]
99,73% der Daten liegen im Intervall: [µ - 3s, µ + 3s]
In der Abbildung sehen Sie, wie diese Intervalle dargestellt werden und in welcher Beziehung sie zueinander stehen, wenn Sie die Breite der Basis des Diagramms erhöhen.
Daher definiert die Anwendung der empirischen Regel im Maßstab einer Standardnormalvariablen z die folgenden Intervalle:
68,27% der Daten liegen im Intervall: [-1, 1]
95,45% der Daten liegen im Intervall: [-2, 2]
99,73% der Daten liegen im Intervall: [-3, 3]
Die empirische Regel erlaubt abgekürzte Berechnungen bei der Arbeit mit einer Normalverteilung.
Angenommen, eine Gruppe von 100 Studenten hat ein Durchschnittsalter von 23 Jahren mit einer Standardabweichung von 2 Jahren. Welche Informationen erlaubt die empirische Regel??
Das Anwenden der empirischen Regel umfasst die folgenden Schritte:
Da der Mittelwert 23 und die Standardabweichung 2 ist, sind die Intervalle:
[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]
[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]
[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]
(100) * 68,27% = ungefähr 68 Studenten
(100) * 95,45% = ungefähr 95 Studenten
(100) * 99,73% = ungefähr 100 Studenten
Mindestens 68 Schüler sind zwischen 21 und 25 Jahre alt.
Mindestens 95 Schüler sind zwischen 19 und 27 Jahre alt.
Fast 100 Schüler sind zwischen 17 und 29 Jahre alt.
Die empirische Regel ist eine schnelle und praktische Methode zur Analyse statistischer Daten, die mit zunehmender Symmetrie der Verteilung immer zuverlässiger wird.
Ihre Nützlichkeit hängt von dem Bereich ab, in dem sie verwendet wird, und von den Fragen, die gestellt werden. Es ist sehr nützlich zu wissen, dass das Auftreten von Werten mit drei Standardabweichungen unter oder über dem Mittelwert fast unwahrscheinlich ist, selbst bei nicht normalen Verteilungsvariablen liegen mindestens 88,8% der Fälle im Intervall von drei Sigma.
In den Sozialwissenschaften ist ein allgemein schlüssiges Ergebnis das Intervall des Mittelwerts plus oder minus zwei Sigma (95%), während in der Teilchenphysik ein neuer Effekt ein Fünf-Sigma-Intervall (99,99994%) erfordert, um als Entdeckung betrachtet zu werden..
In einem Wildreservat gibt es schätzungsweise 16.000 Kaninchen mit einer Standardabweichung von 500 Kaninchen. Wenn die Verteilung der Variablen "Anzahl der Kaninchen in der Reserve" unbekannt ist, kann die Wahrscheinlichkeit geschätzt werden, dass die Kaninchenpopulation zwischen 15.000 und 17.000 Kaninchen liegt?
Das Intervall kann folgendermaßen dargestellt werden:
15000 = 16000 - 1000 = 16000 - 2 (500) = u - 2 s
17000 = 16000 + 1000 = 16000 + 2 (500) = u + 2 s
Deshalb: [15000, 17000] = [µ - 2 s, µ + 2 s]
Unter Anwendung des Satzes von Tchebyshev besteht eine Wahrscheinlichkeit von mindestens 0,75, dass die Kaninchenpopulation im Wildreservat zwischen 15.000 und 17.000 Kaninchen liegt..
Das Durchschnittsgewicht von einjährigen Kindern in einem Land wird normalerweise mit einem Mittelwert von 10 Kilogramm und einer Standardabweichung von ungefähr 1 Kilogramm verteilt.
a) Schätzen Sie den Prozentsatz der einjährigen Kinder im Land, die ein Durchschnittsgewicht zwischen 8 und 12 Kilogramm haben.
8 = 10 - 2 = 10 - 2 (1) = u - 2 s
12 = 10 + 2 = 10 + 2 (1) = u + 2 s
Deshalb: [8, 12] = [µ - 2s, µ + 2s]
Nach der empirischen Regel kann festgestellt werden, dass 68,27% der einjährigen Kinder im Land zwischen 8 und 12 Kilogramm Gewicht haben.
b) Wie hoch ist die Wahrscheinlichkeit, ein einjähriges Kind mit einem Gewicht von 7 kg oder weniger zu finden??
7 = 10 - 3 = 10 - 3 (1) = u - 3 s
Es ist bekannt, dass 7 Kilogramm Gewicht den Wert µ - 3s darstellen, und es ist bekannt, dass 99,73% der Kinder zwischen 7 und 13 Kilogramm Gewicht haben. Damit bleiben nur 0,27% der gesamten Kinder für die Extreme. Die Hälfte von ihnen, 0,135%, sind 7 Kilogramm oder weniger und die andere Hälfte, 0,135%, sind 11 Kilogramm oder mehr.
Daraus kann geschlossen werden, dass es eine Wahrscheinlichkeit von 0,00135 gibt, dass ein Kind 7 Kilogramm oder weniger wiegt.
c) Wenn die Bevölkerung des Landes 50 Millionen Einwohner erreicht und 1-jährige Kinder 1% der Bevölkerung des Landes ausmachen, wie viele einjährige Kinder werden zwischen 9 und 11 Kilogramm wiegen?
9 = 10 - 1 = u - s
11 = 10 + 1 = u + s
Deshalb: [9, 11] = [µ - s, µ + s]
Nach der empirischen Regel befinden sich 68,27% der Einjährigen im Land im Intervall [µ - s, µ + s]
Es gibt 500.000 Einjährige im Land (1% von 50 Millionen), so dass 341.350 Kinder (68,27% von 500.000) zwischen 9 und 11 Kilogramm wiegen.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.