
Was ist akustische Impedanz? Anwendungen und Übungen
Das akustische Impedanz oder eine spezifische akustische Impedanz ist der Widerstand des materiellen Mediums gegen den Durchgang von Schallwellen. Sie ist für ein bestimmtes Medium konstant, das von einer felsigen Schicht im Erdinneren zum biologischen Gewebe gelangt.
Wenn wir die akustische Impedanz als Z bezeichnen, haben wir in mathematischer Form:
Z = ρ.v
Wobei ρ die Dichte und v die Schallgeschwindigkeit des Mediums ist. Dieser Ausdruck gilt für eine ebene Welle, die sich in einer Flüssigkeit bewegt.
In Einheiten des SI International System wird die Dichte in kg / m angegeben3 und die Geschwindigkeit in m / s. Daher betragen die Einheiten der akustischen Impedanz kg / mzwei.s.
Ebenso ist die akustische Impedanz definiert als der Quotient zwischen dem Druck p und der Geschwindigkeit:
Z = p / v
Auf diese Weise ausgedrückt ist Z analog zum elektrischen Widerstand R = V / I, wobei der Druck die Rolle der Spannung und die Geschwindigkeit des Stroms spielt. Andere SI-Einheiten von Z wären Pa.s / m oder N.s / m3, völlig gleichwertig mit den zuvor angegebenen.
Artikelverzeichnis
- 1 Übertragung und Reflexion der Schallwelle
- 1.1 Transmissions- und Reflexionskoeffizienten
- 2 Anwendungen und Übungen
- 2.1 - Aufgabe gelöst 1
- 2.2 - Übung gelöst 2
- 3 Referenzen
Schallwellenübertragung und -reflexion
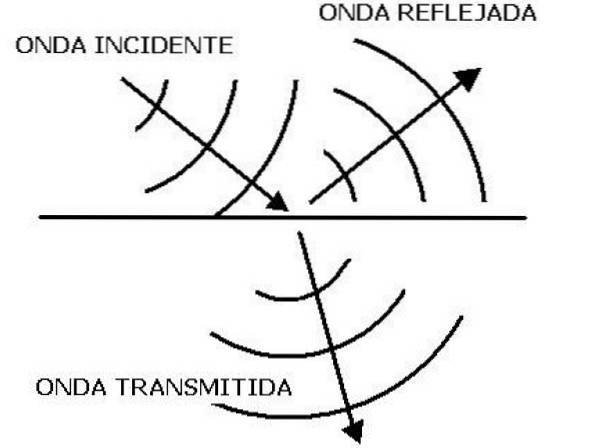
Wenn Sie zwei Mittel mit unterschiedlichen Impedanzen haben Z.1 und Z.zwei, Ein Teil einer Schallwelle, die auf die Schnittstelle von beiden trifft, kann übertragen und ein anderer Teil reflektiert werden. Diese reflektierte Welle oder dieses Echo enthält wichtige Informationen über das zweite Medium..
Die Art und Weise, wie die von der Welle transportierte Energie verteilt wird, hängt von den Reflexionskoeffizienten R und dem Transmissionskoeffizienten T ab, zwei sehr nützliche Größen zur Untersuchung der Ausbreitung der Schallwelle. Für den Reflexionskoeffizienten ist es der Quotient:
R = I.r / ICHoder
Wo ichoder ist die Intensität der einfallenden Welle und ichr ist die Intensität der reflektierten Welle. Ebenso haben wir den Transmissionskoeffizienten:
T = I.t / ICHoder
Nun kann gezeigt werden, dass die Intensität einer ebenen Welle proportional zu ihrer Amplitude A ist:
I = (1/2) Z.ωzwei .ZUzwei
Dabei ist Z die akustische Impedanz des Mediums und ω die Frequenz der Welle. Andererseits ist der Quotient zwischen der übertragenen Amplitude und der einfallenden Amplitude:
ZUt/ZUoder = 2Z1/ (Z.1 +Z.zwei)
Welches erlaubt den Quotienten I.t / ICHoder wird ausgedrückt als Amplitude der einfallenden und übertragenen Wellen als:
icht / ICHoder = Z.zweiZUtzwei / Z.1ZUoderzwei
Mit diesen Ausdrücken werden R und T in Bezug auf die akustische Impedanz Z erhalten.
Transmissions- und Reflexionskoeffizienten
Der obige Quotient ist genau der Transmissionskoeffizient:
T = (Z.zwei/ Z.1) [2.Z.1/ (Z.1 +Z.zwei)]zwei = 4Z1Z.zwei / (Z.1 +Z.zwei)zwei
Da keine Verluste in Betracht gezogen werden, ist die einfallende Intensität zwar die Summe der übertragenen Intensität und der reflektierten Intensität:
ichoder = Ichr + icht → (I.r / ICHoder) + (I.t / ICHoder) = 1
Dies ermöglicht es uns, einen Ausdruck für den Reflexionskoeffizienten in Bezug auf die Impedanzen der beiden Medien zu finden:
R + T = 1 → R = 1 - T.
Wenn Sie eine kleine Algebra ausführen, um die Terme neu zu ordnen, beträgt der Reflexionskoeffizient:
R = 1 - 4Z1Z.zwei / (Z.1 +Z.zwei)zwei = (Z.1 - Z.zwei)zwei/ (Z.1 +Z.zwei)zwei
Und da die Informationen, die sich auf das zweite Medium beziehen, im reflektierten Impuls gefunden werden, ist der Reflexionskoeffizient von großem Interesse..
Wenn also die beiden Medien einen großen Impedanzunterschied aufweisen, wird der Zähler des vorherigen Ausdrucks größer. Dann ist die Intensität der reflektierten Welle hoch und enthält gute Informationen über das Medium..
Der Teil der Welle, der auf dieses zweite Medium übertragen wird, verblasst allmählich und die Energie wird als Wärme abgegeben..
Anwendungen und Übungen
Transmissions- und Reflexionsphänomene führen zu mehreren sehr wichtigen Anwendungen, beispielsweise Sonar, das während des Zweiten Weltkriegs entwickelt und zur Erkennung von Objekten verwendet wurde. Übrigens haben einige Säugetiere wie Fledermäuse und Delfine ein eingebautes Sonarsystem.
Diese Eigenschaften werden auch häufig verwendet, um das Erdinnere bei seismischen Prospektionsmethoden, bei der medizinischen Ultraschallbildgebung, bei der Messung der Knochendichte und bei der Abbildung verschiedener Strukturen auf Fehler und Defekte zu untersuchen..
Die akustische Impedanz ist auch ein wichtiger Parameter bei der Bewertung des Klangverhaltens eines Musikinstruments..
- Gelöste Übung 1
Die Ultraschalltechnik zur Abbildung von biologischem Gewebe verwendet hochfrequente Schallimpulse. Die Echos enthalten Informationen über die Organe und Gewebe, die sie durchlaufen und die von einer Software für die Übersetzung in ein Bild verantwortlich sind.
Ein Ultraschallimpuls, der auf die Fett-Muskel-Grenzfläche gerichtet ist, wird eingeschnitten. Mit den bereitgestellten Daten finden Sie:
a) Die akustische Impedanz jedes Gewebes.
b) Der Prozentsatz des Ultraschalls, der an der Grenzfläche zwischen Fett und Muskel reflektiert wird.
Fett
- Dichte: 952 kg / m3
- Schallgeschwindigkeit: 1450 m / s
Muskel
- Dichte: 1075 kg / m3
- Schallgeschwindigkeit: 1590 m / s
Lösung für
Die akustische Impedanz jedes Gewebes wird durch Ersetzen in der Formel ermittelt:
Z = ρ.v
Auf diese Weise:
Z.Fett = 952 kg / m3 x 1450 m / s = 1,38 x 106 kg / mzwei.s
Z.Muskel = 1075 kg / m3 x 1590 m / s = 1,71 x 106 kg / mzwei.s
Lösung b
Um den Prozentsatz der Intensität zu ermitteln, der an der Grenzfläche der beiden Gewebe reflektiert wird, wird der Reflexionskoeffizient verwendet, der gegeben ist durch:
R = (Z.1 - Z.zwei)zwei/ (Z.1 +Z.zwei)zwei
Hier Z.Fett = Z.1 und Z.Muskel = Z.zwei. Der Reflexionskoeffizient ist eine positive Größe, die durch die Quadrate in der Gleichung garantiert wird.
Ersetzen und bewerten:
R = (1,38 · 10)6 - 1,71 x 106 )zwei / (1,38 x 106 + 1,71 x 106 )zwei = 0,0114.
Wenn wir mit 100 multiplizieren, wird der Prozentsatz reflektiert: 1,14% der Einfallsintensität.
- Übung gelöst 2
Eine Schallwelle hat eine Intensität von 100 Dezibel und fällt normalerweise auf die Wasseroberfläche. Bestimmen Sie den Intensitätspegel der übertragenen Welle und den der reflektierten Welle.
Daten:
Wasser
- Dichte: 1000 kg / m3
- Schallgeschwindigkeit: 1430 m / s
Luft
- Dichte: 1,3 kg / m3
- Schallgeschwindigkeit: 330 m / s
Lösung
Der Intensitätspegel in Dezibel einer Schallwelle wird als L bezeichnet, ist dimensionslos und wird durch die folgende Formel angegeben:
L = 10 log (I / 10-12)
Auf beiden Seiten auf 10 erhöhen:
10 L / 10 = I / 10-12
Da L = 100 ist, ergibt sich:
I / 10-12 = 1010
Intensitätseinheiten werden als Leistung pro Flächeneinheit angegeben. Im internationalen System sind sie Watt / mzwei. Daher ist die Intensität der einfallenden Welle:
ichoder = 1010 . 10-12 = 0,01 W / mzwei.
Um die Intensität der übertragenen Welle zu ermitteln, wird der Übertragungskoeffizient berechnet und dann mit der einfallenden Intensität multipliziert.
Die jeweiligen Impedanzen sind:
Z.Wasser = 1000 kg / m3 x 1430 m / s = 1,43 x 106 kg / mzwei.s
Z.Luft = 1,3 kg / m3 x 330 m / s = 429 kg / mzwei.s
Ersetzen und bewerten in:
T = 4Z1Z.zwei / (Z.1 +Z.zwei)zwei = 4 × 1,43 × 106 x 429 / (1,43 x 106 + 429)zwei = 1,12 x 10-3
Die Intensität der übertragenen Welle ist also:
icht = 1,12 x 10-3 x 0,01 W / mzwei = 1,12 x 10-5 W / mzwei
Sein Intensitätsniveau in Dezibel wird berechnet durch:
L.t = 10 log (I.t / 10-12) = 10 log (1,12 x 10)-5 / 10-12) = 70,3 dB
Der Reflexionskoeffizient beträgt seinerseits:
R = 1 - T = 0,99888
Damit ist die Intensität der reflektierten Welle:
ichr = 0,99888 × 0,01 W / mzwei = 9,99 x 10-3 W / mzwei
Und seine Intensität ist:
L.t = 10 log (I.r / 10-12) = 10 log (9,99 x 10)-3 / 10-12) = 100 dB
Verweise
- Andriessen, M. 2003. HSC-Physikkurs. Palisander.
- Baranek, L. 1969. Akustik. Zweite Ausgabe. Editorial Hispano Americana.
- Kinsler, L. 2000. Grundlagen der Akustik. Wiley und Söhne.
- Lowrie, W. 2007. Grundlagen der Geophysik. 2 .. Auflage. Cambridge University Press.
- Wikipedia. Akustische Impedanz. Wiederhergestellt von: en.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.