Was ist die Vektormenge? (Mit Beispielen)

Es definiert die Anzahl der Vektoren, oder Vektor, wie derjenige, für den es notwendig ist, sowohl seine Größe oder sein Modul (mit den jeweiligen Einheiten) als auch seine Richtung anzugeben.

Im Gegensatz zur Vektorgröße hat eine skalare Größe nur die Größe (und Einheiten), aber keine Richtung. Einige Beispiele für skalare Größen sind unter anderem Temperatur, Volumen eines Objekts, Länge, Masse und Zeit..

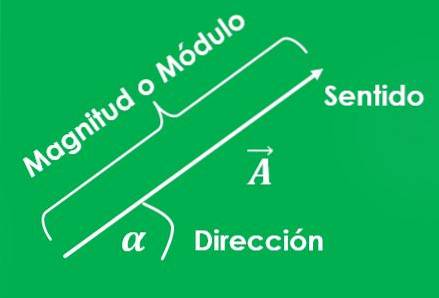
Unterschied zwischen Vektorgröße und Skalar

Im folgenden Beispiel können Sie lernen, eine skalare Größe von einer Vektorgröße zu unterscheiden:

Eine Geschwindigkeit von 10 km / h ist eine skalare Größe, während eine Geschwindigkeit von 10 km / h nach Norden eine Vektorgröße ist. Der Unterschied besteht darin, dass im zweiten Fall zusätzlich zur Größe eine Richtung angegeben wird.

Vektorgrößen haben eine unendliche Anzahl von Anwendungen, insbesondere in der Welt der Physik.

Diagramme und Bezeichnungen einer Vektormenge

Die Bezeichnung einer Vektorgröße erfolgt durch Platzieren eines Pfeils (→) auf dem zu verwendenden Buchstaben oder durch Fettdruck des Buchstabens (→).zu).

Um eine Vektorgröße grafisch darzustellen, benötigen Sie ein Referenzsystem. In diesem Fall wird die kartesische Ebene als Referenzsystem verwendet.

Der Graph eines Vektors ist eine Linie, deren Länge die Größe darstellt; und der Winkel zwischen der Linie und der X-Achse, gemessen gegen den Uhrzeigersinn, repräsentiert seine Richtung.

Sie müssen angeben, welcher der Startpunkt des Vektors und welcher der Ankunftspunkt ist. Am Ende der Linie befindet sich außerdem ein Pfeil, der auf den Ankunftspunkt zeigt und die Richtung des Vektors angibt.

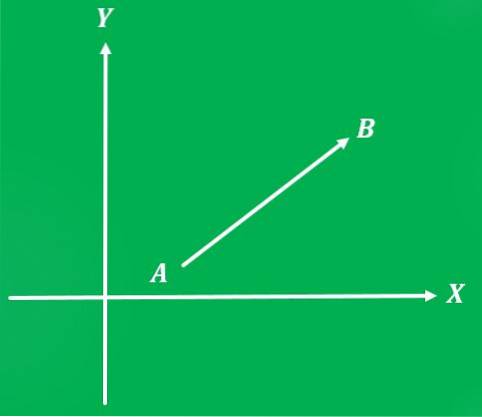
Sobald ein Referenzsystem festgelegt wurde, kann der Vektor als geordnetes Paar geschrieben werden: Die erste Koordinate repräsentiert seine Größe und die zweite Koordinate seine Richtung..

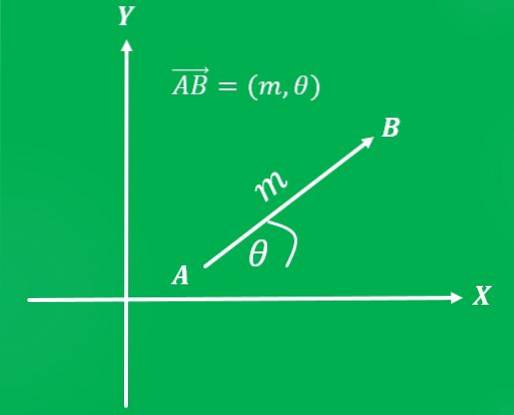
Beispiele

1- Schwerkraft, die auf ein Objekt wirkt

Wenn sich ein Objekt in einer Höhe von 2 Metern über dem Boden befindet und freigegeben wird, wirkt die Schwerkraft mit einer Größe von 9,8 m / s² und einer Richtung senkrecht zum Boden nach unten auf ihn.

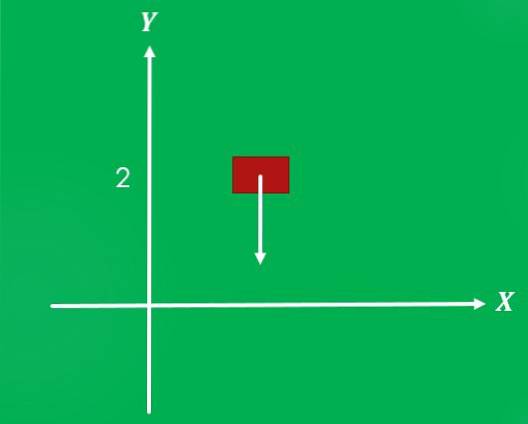
2- Bewegung eines Flugzeugs

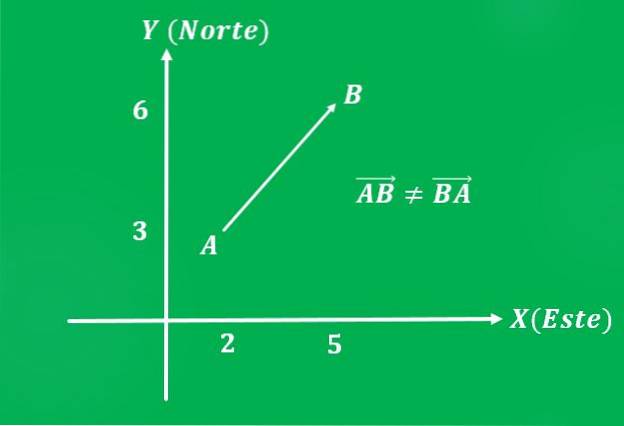
Ein Flugzeug, das mit einer Geschwindigkeit von 650 km / h (Größe) von Punkt A = (2,3) nach Punkt B = (5,6) des kartesischen Flugzeugs flog. Die Richtung der Flugbahn ist 45º nordöstlich (Richtung).

Es sollte beachtet werden, dass, wenn die Reihenfolge der Punkte umgekehrt wird, der Vektor die gleiche Größe und die gleiche Richtung hat, aber einen anderen Sinn, der südwestlich sein wird.

3- Auf ein Objekt ausgeübte Kraft

Juan beschließt, einen Stuhl mit einer Kraft von 10 Pfund in eine Richtung parallel zum Boden zu schieben. Die möglichen Richtungen der ausgeübten Kraft sind: links oder rechts (im Fall der kartesischen Ebene).

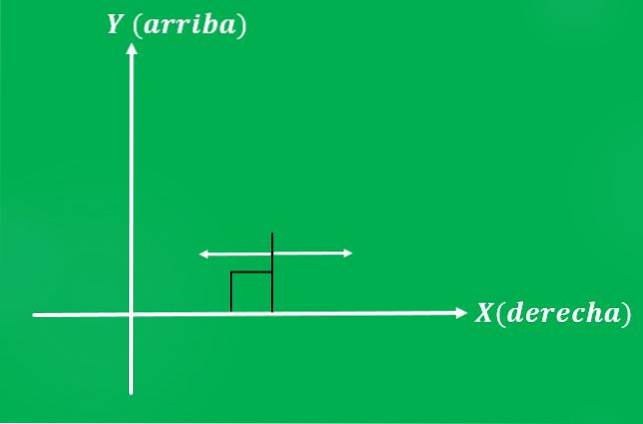
Wie im vorherigen Beispiel führt das Gefühl, dass Juan beschließt, die Kraft zu geben, zu einem anderen Ergebnis.

Dies sagt uns, dass zwei Vektoren die gleiche Größe und Richtung haben können, aber unterschiedlich sind (sie führen zu unterschiedlichen Ergebnissen)..

Es können zwei oder mehr Vektoren addiert und subtrahiert werden, für die es sehr nützliche Ergebnisse gibt, wie beispielsweise das Gesetz des Parallelogramms. Sie können einen Vektor auch mit einem Skalar multiplizieren.

Verweise

1. A. Barragan, G. Cerpa, M. Rodríguez & H. Núñez (2006). Physik für die High School Cinematics. Pearson Ausbildung.
2. Ford, K. W. (2016). Grundphysik: Lösungen zu den Übungen. World Scientific Publishing Company.
3. Giancoli, D. C. (2006). Physik: Prinzipien mit Anwendungen. Pearson Ausbildung.
4. A. L. Gómez & H. N. Trejo (2006). Physik l, Ein konstruktivistischer Ansatz. Pearson Ausbildung.
5. Serway, R. A. & Faughn, J. S. (2001). Körperlich. Pearson Ausbildung.
6. Stroud, K. A. & Booth, D. J. (2005). Vektoranalyse (Illustrierte Ausgabe). Industrial Press Inc..
7. Wilson, J. D. & Buffa, A. J. (2003). Körperlich. Pearson Ausbildung.