Das Rang, Entfernung oder Amplitude ist in der Statistik die Differenz (Subtraktion) zwischen dem Maximalwert und dem Minimalwert eines Datensatzes aus einer Stichprobe oder einer Population. Wenn der Bereich durch den Buchstaben R und die Daten durch dargestellt wird x, Die Formel für den Bereich lautet einfach:
R = xmax - xMindest
Wo xmax ist der Maximalwert der Daten und xMindest ist das Minimum.
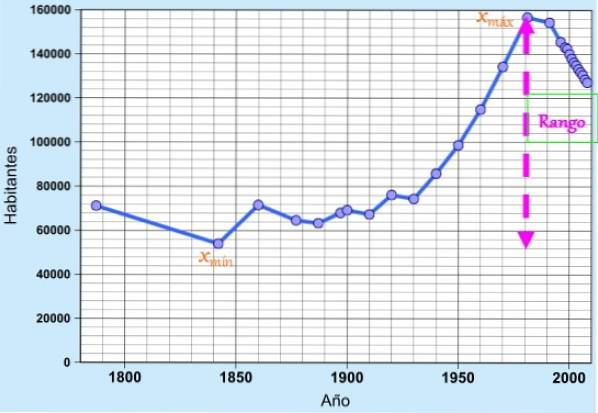
Das Konzept ist als einfaches Maß für die Streuung sehr nützlich, um die Variabilität der Daten schnell zu erkennen, da es die Ausdehnung oder Länge des Intervalls angibt, in dem diese gefunden werden..
Angenommen, die Größe einer Gruppe von 25 männlichen Ingenieurstudenten im ersten Studienjahr an einer Universität wird gemessen. Der größte Schüler in der Gruppe ist 1,93 m und der kürzeste 1,67 m. Dies sind die Extremwerte der Probendaten, daher lautet ihr Pfad:
R = 1,93 - 1,67 m = 0,26 m oder 26 cm.
Die Größe der Schüler in dieser Gruppe verteilt sich auf diesen Bereich.
Artikelverzeichnis
Die Reichweite ist, wie bereits erwähnt, ein Maß für die Verteilung der Daten. Ein kleiner Bereich zeigt an, dass die Daten mehr oder weniger nahe beieinander liegen und nur eine geringe Streuung vorliegt. Andererseits zeigt ein größerer Bereich an, dass die Daten stärker verteilt sind..
Die Vorteile der Berechnung des Bereichs liegen auf der Hand: Es ist sehr einfach und schnell zu finden, da es sich um einen einfachen Unterschied handelt.
Es hat auch die gleichen Einheiten wie die Daten, mit denen es arbeitet, und das Konzept ist für jeden Beobachter sehr einfach zu interpretieren..
Im Beispiel der Größe von Ingenieurstudenten würden wir bei einer Reichweite von 5 cm sagen, dass die Studenten alle ungefähr gleich groß sind. Bei einer Reichweite von 26 cm gehen wir jedoch sofort davon aus, dass sich in der Stichprobe Schüler aller mittleren Höhen befinden. Ist diese Annahme immer richtig??
Wenn wir genau hinschauen, kann es sein, dass in unserer Stichprobe von 25 Ingenieurstudenten nur einer von ihnen 1,93 misst und die restlichen 24 Höhen nahe 1,67 m haben.
Und doch bleibt die Reichweite gleich, obwohl das Gegenteil durchaus möglich ist: Die Höhe der Mehrheit liegt bei 1,90 m und nur eine bei 1,67 m.
In beiden Fällen ist die Verteilung der Daten sehr unterschiedlich.
Die Nachteile des Bereichs als Maß für die Dispersion liegen darin, dass nur Extremwerte verwendet werden und alle anderen ignoriert werden. Da die meisten Informationen verloren gehen, wissen Sie nicht, wie die Beispieldaten verteilt werden.
Ein weiteres wichtiges Merkmal ist, dass der Bereich der Probe niemals abnimmt. Wenn wir mehr Informationen hinzufügen, dh mehr Daten berücksichtigen, erhöht sich der Bereich oder bleibt gleich.
In jedem Fall ist es nur nützlich, wenn mit kleinen Proben gearbeitet wird. Die alleinige Verwendung als Maß für die Dispersion in großen Proben wird nicht empfohlen..
Was Sie tun müssen, ist die Berechnung anderer Dispersionsmaße, die die Informationen berücksichtigen, die durch die Gesamtdaten bereitgestellt werden: Route Interquartil, Varianz, Standardabweichung und Variationskoeffizient.
Wir haben erkannt, dass die Schwäche des Bereichs als Maß für die Streuung darin besteht, dass nur die Extremwerte der Datenverteilung verwendet werden und die anderen weggelassen werden..
Um diese Unannehmlichkeiten zu vermeiden, muss die Quartile: drei Werte bekannt als Positionsmessungen.
Sie verteilen die nicht gruppierten Daten in vier Teile (andere weit verbreitete Positionsmaße sind Dezile und der Perzentile). Dies sind seine Eigenschaften:
-Das erste Quartil Q.1 ist der Wert der Daten, so dass 25% von allen kleiner als Q sind1.
-Das zweite Quartil Q.zwei ist der Median der Verteilung, was bedeutet, dass die Hälfte (50%) der Daten kleiner als dieser Wert ist.
-Schließlich das dritte Quartil Q.3 weist darauf hin, dass 75% der Daten kleiner als Q sind3.
Dann wird der Interquartilbereich oder Interquartilbereich als die Differenz zwischen dem dritten Quartil Q definiert3 und das erste Quartil Q.1 der Daten:
Interquartilbereich = R.Q. = Q.3 - Q.1
Auf diese Weise wird der Wert des Bereichs R.Q. es ist nicht so stark von Extremwerten betroffen. Aus diesem Grund ist es ratsam, es zu verwenden, wenn es sich um verzerrte Verteilungen handelt, wie z. B. die oben beschriebenen sehr großen oder sehr kleinen Schüler..
Es gibt verschiedene Möglichkeiten, sie zu berechnen. Hier werden wir eine vorschlagen, aber in jedem Fall ist es notwendig, die zu kennen Anzahl der Bestellungen "N.oder”, Welches ist der Platz, den das jeweilige Quartil in der Verteilung einnimmt.
Das heißt, wenn zum Beispiel der Term, der Q entspricht1 ist die zweite, dritte oder vierte usw. der Verteilung.
N.oder (Q.1) = (N + 1) / 4
N.oder (Q.zwei) = (N + 1) / 2
N.oder (Q.3) = 3 (N + 1) / 4
Wobei N die Anzahl der Daten ist.
Der Median ist der Wert, der genau in der Mitte der Verteilung liegt. Wenn die Anzahl der Daten ungerade ist, ist es kein Problem, sie zu finden. Wenn sie jedoch gerade sind, werden die beiden zentralen Werte gemittelt, um eins zu werden.
Sobald die Bestellnummer berechnet wurde, wird eine dieser drei Regeln befolgt:
-Wenn keine Dezimalstellen vorhanden sind, werden die in der Verteilung angegebenen Daten durchsucht, und dies ist das gesuchte Quartil.
-Wenn die Bestellnummer auf halbem Weg zwischen zwei liegt, werden die durch den ganzzahligen Teil angegebenen Daten mit den folgenden Daten gemittelt, und das Ergebnis ist das entsprechende Quartil.
-In jedem anderen Fall wird es auf die nächste ganze Zahl gerundet, und das ist die Position des Quartils.
Auf einer Skala von 0 bis 20 erhielt eine Gruppe von 16 Mathematik-I-Schülern bei einer Zwischenprüfung die folgenden Punkte (Punkte):
16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14
Finden:
a) Der Bereich oder die Reichweite der Daten.
b) Die Werte der Quartile Q.1 und Q.3
c) Der Interquartilbereich.
Um den Pfad zu finden, müssen Sie zunächst die Daten in aufsteigender oder absteigender Reihenfolge anordnen. Zum Beispiel in aufsteigender Reihenfolge haben Sie:
1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20
Verwenden Sie die am Anfang angegebene Formel: R = xmax - xMindest
R = 20 - 1 Punkte = 19 Punkte.
Entsprechend dem Ergebnis weisen diese Qualifikationen eine große Streuung auf.
N = 16
N.oder (Q.1) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4,25
Es ist eine Zahl mit Dezimalstellen, deren ganzzahliger Teil 4 ist. Dann gehen wir zur Verteilung, suchen nach den Daten, die den vierten Platz einnehmen, und ihr Wert wird mit dem der fünften Position gemittelt. Da beide 9 sind, beträgt der Durchschnitt auch 9 und so:
Q.1 = 9
Jetzt wiederholen wir den Vorgang, um Q zu finden3::
N.oder (Q.3) = 3 (N + 1) / 4 = 3 (16 + 1) / 4 = 12,75
Wieder ist es eine Dezimalstelle, aber da es nicht die Hälfte ist, wird es auf 13 gerundet. Das Quartil, das wir suchen, nimmt die dreizehnte Position ein und ist:
Q.3 = 16
R.Q. = Q.3 - Q.1 = 16 - 9 = 7 Punkte.
Was, wie wir sehen, viel kleiner ist als der in Abschnitt a) berechnete Datenbereich, da die Mindestpunktzahl 1 Punkt betrug, ein Wert, der viel weiter vom Rest entfernt ist..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.