
Erklärung der zusammengesetzten Proportionalität, zusammengesetzte Dreierregel, Übungen
Das zusammengesetzte oder mehrfache Proportionalität Es ist die Beziehung zwischen mehr als zwei Größen, bei der eine direkte und inverse Proportionalität zwischen den Daten und dem Unbekannten beobachtet werden kann. Dies ist eine fortgeschrittenere Version der einfachen Proportionalität, obwohl die in beiden Verfahren verwendeten Techniken ähnlich sind..
Wenn zum Beispiel 7 Personen benötigt werden, um 10 Tonnen Waren in 3 Stunden zu entladen, kann die zusammengesetzte Proportionalität verwendet werden, um zu berechnen, wie viele Personen benötigt werden, um 15 Tonnen in 4 Stunden zu entladen..
Um diese Frage zu beantworten, ist es zweckmäßig, eine Wertetabelle zu erstellen, um die Größen und Unbekannten zu untersuchen und in Beziehung zu setzen.
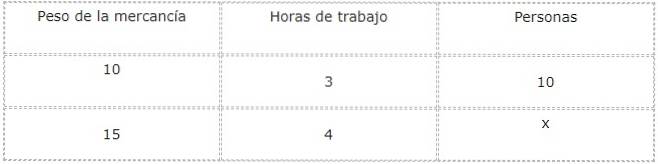
Wir analysieren nun die Arten von Beziehungen zwischen jeder Größe und dem gegenwärtigen Unbekannten, was in diesem Fall der Anzahl der Personen entspricht, die arbeiten werden.
Mit zunehmendem Gewicht der Ware steigt auch die Anzahl der Personen, die zum Entladen erforderlich sind. Aus diesem Grund ist die Beziehung zwischen Gewicht und Arbeitern direkt.
Andererseits nimmt die Arbeitszeit mit zunehmender Anzahl von Arbeitnehmern ab. Aus diesem Grund ist das Verhältnis zwischen Menschen und Arbeitsstunden umgekehrt.
Artikelverzeichnis
- 1 Berechnung der zusammengesetzten Proportionalitäten
- 2 Erläuterung
- 3 Direkte Dreierregel
- 4 Umgekehrte Dreierregel
- 5 Zustand
- 6 Überprüfung der Ergebnisse
- 7 Freigabe
- 8 Geschichte
- 9 Gelöste Übungen
- 9.1 Übung 1
- 9.2 Übung 2
- 10 Vorgeschlagene Übungen
- 11 Referenzen
Wie man zusammengesetzte Proportionalitäten berechnet
Um Beispiele wie das obige zu lösen, wird meistens die zusammengesetzte Regel der Drei-Methode verwendet. Dies besteht darin, die Arten von Beziehungen zwischen Größen und Unbekannten zu ermitteln und dann ein Produkt zwischen Brüchen darzustellen.
In Bezug auf das ursprüngliche Beispiel sind die der Wertetabelle entsprechenden Brüche wie folgt organisiert:
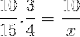
Vor dem Lösen und Lösen des Unbekannten müssen jedoch die der umgekehrten Beziehung entsprechenden Brüche invertiert werden. Welche für diesen Fall der variablen Zeit entsprechen. Auf diese Weise ist die zu lösende Operation:
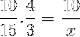
Wessen einziger Unterschied ist die Inversion des Bruchteils, der der Zeitvariablen 4/3 entspricht. Wir fahren fort zu arbeiten und löschen den Wert von x.
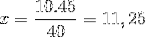
Daher werden mehr als elf Personen benötigt, um 15 Tonnen Waren in 4 Stunden oder weniger entladen zu können.
Erläuterung
Die Proportionalität ist die konstante Beziehung zwischen sich ändernden Größen, die für jede der beteiligten Größen symmetrisch ist. Es gibt direkt und umgekehrt proportionale Beziehungen, wodurch die Parameter der einfachen oder zusammengesetzten Proportionalität definiert werden.
Direkte Dreierregel
Es besteht aus einer Proportionsbeziehung zwischen Variablen, die beim Ändern dasselbe Verhalten zeigen. Es ist sehr häufig bei der Berechnung von Prozentsätzen, die sich auf andere Größen als einhundert beziehen, wobei seine Grundstruktur geschätzt wird.
Beispielsweise können 15% von 63 berechnet werden. Auf den ersten Blick kann dieser Prozentsatz nicht leicht eingeschätzt werden. Bei Anwendung der Dreierregel kann jedoch die folgende Beziehung hergestellt werden: Wenn 100% 63 ist, dann 15%, wie viel wird es sein?
100% - 63
15% -X
Und die entsprechende Operation ist:
(15%, 63) / 100% = 9,45
Wenn die Prozentzeichen vereinfacht werden und die Zahl 9.45 erhalten wird, entspricht dies 15% von 63.
Umgekehrte Dreierregel
Wie der Name schon sagt, ist in diesem Fall die Beziehung zwischen den Variablen umgekehrt. Die umgekehrte Beziehung muss hergestellt werden, bevor mit der Berechnung fortgefahren werden kann. Sein Verfahren ist homolog zu dem der direkten Dreierregel, mit Ausnahme der Investition in die zu berechnende Fraktion..
Zum Beispiel benötigen 3 Maler 5 Stunden, um eine Wand fertig zu stellen. In wie vielen Stunden würden 4 Maler es beenden?
In diesem Fall ist die Beziehung umgekehrt, da mit zunehmender Anzahl von Malern die Arbeitszeit abnehmen sollte. Die Beziehung wird hergestellt;
3 Maler - 5 Stunden
4 Maler - X Stunden
Wenn die Beziehung umgekehrt wird, wird die Reihenfolge der Operation umgekehrt. Dies ist der richtige Weg;
(3 Maler). (5 Stunden) / 4 Maler = 3,75 Stunden
Der Begriff Maler wird vereinfacht und das Ergebnis ist 3,75 Stunden.
Bedingung
Um in Gegenwart einer Verbindung oder einer Mehrfachproportionalität zu sein, müssen beide Arten von Beziehungen zwischen den Größen und Variablen gefunden werden.
- Direkt: Die Variable hat das gleiche Verhalten wie die unbekannte. Das heißt, wenn einer zunimmt oder abnimmt, ändert sich der andere gleichermaßen.
- Invers: Die Variable zeigt ein Antonyme-Verhalten gegenüber dem Unbekannten. Der Bruch, der diese Variable in der Wertetabelle definiert, muss invertiert werden, um die umgekehrt proportionale Beziehung zwischen Variable und Unbekanntem darzustellen..
Überprüfung der Ergebnisse
Es ist sehr üblich, die Reihenfolge der Größen zu verwechseln, wenn mit zusammengesetzten Proportionalitäten gearbeitet wird, im Gegensatz zu den üblichen Proportionsberechnungen, deren Natur meist direkt und durch eine einfache Dreierregel lösbar ist..
Aus diesem Grund ist es wichtig, die logische Reihenfolge der Ergebnisse zu untersuchen und die Kohärenz der nach der Dreierregel erstellten Zahlen zu überprüfen.
Im ersten Beispiel würde ein solcher Fehler zu 20 führen. Das heißt, 20 Personen entladen 15 Tonnen Waren in 4 Stunden.
Auf den ersten Blick scheint es kein verrücktes Ergebnis zu sein, aber es ist merkwürdig, dass der Personalbestand um fast 200% (von 7 auf 20 Personen) steigt, wenn der Warenzuwachs 50% beträgt, und dies sogar mit einer größeren Zeitspanne bis die Arbeit ausführen.
Auf diese Weise stellt die logische Überprüfung der Ergebnisse einen wichtigen Schritt bei der Implementierung der Regel der drei Verbindungen dar..
Spielraum
Obwohl die Freigabe in Bezug auf die mathematische Ausbildung grundlegender ist, stellt sie in Fällen der Verhältnismäßigkeit einen wichtigen Schritt dar. Eine falsche Freigabe reicht aus, um ein Ergebnis ungültig zu machen, das mit der einfachen oder zusammengesetzten Dreierregel erzielt wurde..
Geschichte
Die Dreierregel wurde im Westen durch die Araber mit Veröffentlichungen verschiedener Autoren bekannt. Unter ihnen Al-Jwarizmi und Al-Biruni.
Al-Biruni hatte dank seines multikulturellen Wissens Zugang zu umfangreichen Informationen über diese Praxis auf seinen Reisen nach Indien und war für die umfangreichste Dokumentation der Dreierregel verantwortlich.
Er argumentiert in seiner Forschung, dass Indien der erste Ort war, an dem die Anwendung der Dreierregel üblich wurde. Der Autor versichert, dass es in seinen direkten, inversen und sogar komponierten Versionen auf flüssige Weise ausgeführt wurde..
Das genaue Datum, an dem die Dreierregel Teil des mathematischen Wissens Indiens wurde, ist noch unbekannt. Das älteste Dokument, das sich mit dieser Praxis befasst, das Bakhshali-Manuskript, wurde jedoch 1881 entdeckt. Es befindet sich derzeit in Oxford.
Viele Mathematikhistoriker behaupten, dass dieses Manuskript vom Beginn der heutigen Zeit stammt..
Gelöste Übungen
Übung 1
Eine Fluggesellschaft muss 1.535 Personen befördern. Es ist bekannt, dass es mit 3 Flugzeugen 12 Tage dauern würde, bis der letzte Passagier das Ziel erreicht. 450 weitere Personen sind bei der Fluggesellschaft angekommen und 2 Flugzeuge müssen repariert werden, um bei dieser Aufgabe zu helfen. Wie viele Tage benötigt die Fluggesellschaft, um den letzten Passagier an ihr Ziel zu bringen??
Das Verhältnis zwischen der Anzahl der Personen und den Arbeitstagen ist direkt, denn je größer die Anzahl der Personen ist, desto mehr Tage werden für die Ausführung dieser Arbeit benötigt..
Andererseits ist das Verhältnis zwischen Flugzeugen und Tagen umgekehrt proportional. Mit zunehmender Anzahl von Flugzeugen verringern sich die Tage, die für den Transfer aller Passagiere benötigt werden.
Die Wertetabelle für diesen Fall wird erstellt.

Wie im ersten Beispiel ausgeführt, müssen der Zähler und der Nenner in dem Bruch invertiert werden, der der inversen Variablen in Bezug auf das Unbekannte entspricht. Die Operation ist wie folgt:
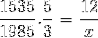
X = 71460/7675 = 9,31 Tage
Der Transfer von 1985 Personen mit 5 Flugzeugen dauert mehr als 9 Tage.
Übung 2
Eine 25-Tonnen-Maisernte wird zu den Lastwagen gebracht. Es ist bekannt, dass sie im Vorjahr 8 Stunden mit einer Lohnsumme von 150 Arbeitern gebraucht haben. Wenn in diesem Jahr die Lohnsumme um 35% gestiegen ist, wie lange wird es dauern, bis die Lastwagen mit einer Ernte von 40 Tonnen gefüllt sind??
Vor der Darstellung der Wertetabelle muss die Anzahl der Arbeitnehmer für dieses Jahr festgelegt werden. Dies stieg um 35% gegenüber der ursprünglichen Zahl von 150 Arbeitnehmern. Hierfür wird eine direkte Dreierregel verwendet.
100% - 150
35% - X.
X = (35.100) / 100 = 52,5. Dies ist die Anzahl der zusätzlichen Arbeitnehmer im Vergleich zum Vorjahr, die nach Rundung des erhaltenen Betrags eine Gesamtzahl von 203 Arbeitnehmern erhalten.
Wir definieren die entsprechende Datentabelle

In diesem Fall stellt das Gewicht eine Variable dar, die in direktem Zusammenhang mit der unbekannten Zeit steht. Andererseits hat die Arbeitervariable eine umgekehrte Beziehung zur Zeit. Je mehr Arbeitnehmer beschäftigt sind, desto kürzer ist der Arbeitstag.
Unter Berücksichtigung dieser Überlegungen und Umkehren des der Arbeitervariablen entsprechenden Bruchteils fahren wir mit der Berechnung fort.
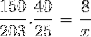
X = 40600/6000 = 6,76 Stunden
Der Tag dauert knapp 7 Stunden.
Vorgeschlagene Übungen
- Definieren Sie 73% von 2875.
- Berechnen Sie die Anzahl der Stunden, die Teresa schläft, wenn bekannt ist, dass sie nur 7% der Gesamtstunden des Tages schläft. Definieren Sie, wie viele Stunden Sie pro Woche schlafen.
- Eine Zeitung veröffentlicht alle 5 Stunden 2000 Exemplare mit nur 2 Druckmaschinen. Wie viele Exemplare wird er in 1 Stunde produzieren, wenn er 7 Maschinen benutzt? Wie lange dauert es 10.000 Kopien mit 4 Maschinen?
Verweise
- Enzyklopädie Alvarez-Initiation. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Vollständige Bedienungsanleitung für Grundschulen und höhere Grundschulen: für angehende Lehrer und insbesondere für Schüler der normalen Schulen der Provinz, Band 1. Joaquín Avendaño. Druck von D. Dionisio Hidalgo, 1844.
- Rationale Approximation realer Funktionen. P.P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. März. 2011.
- Grundrechenarten für den Unterricht an Schulen und Hochschulen in Mittelamerika. Darío González. Trinkgeld. Arenales, 1926.
- Das Studium der Mathematik: Über das Studium und die Schwierigkeiten der Mathematik. Augustus De Morgan. Baldwin und Cradock, 1830.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.