Das Eigenschaften der Gleichheit beziehen sich auf die Beziehung zwischen zwei mathematischen Objekten, unabhängig davon, ob es sich um Zahlen oder Variablen handelt. Es wird durch das Symbol "=" gekennzeichnet, das sich immer in der Mitte dieser beiden Objekte befindet. Dieser Ausdruck wird verwendet, um festzustellen, dass zwei mathematische Objekte dasselbe Objekt darstellen. mit anderen Worten, dass zwei Objekte dasselbe sind.
Es gibt Fälle, in denen es trivial ist, Gleichheit zu verwenden. Zum Beispiel ist klar, dass 2 = 2 ist. Wenn es jedoch um Variablen geht, ist dies nicht mehr trivial und hat spezifische Verwendungszwecke. Wenn wir zum Beispiel y = x und andererseits x = 7 haben, können wir auch daraus schließen, dass y = 7 ist.
Das obige Beispiel basiert auf einer der Eigenschaften der Gleichheit, wie Sie in Kürze sehen werden. Diese Eigenschaften sind wichtig, um Gleichungen (Gleichungen mit Variablen) zu lösen, die einen sehr wichtigen Teil der Mathematik bilden..
Artikelverzeichnis
Die reflexive Eigenschaft besagt im Fall der Gleichheit, dass jede Zahl gleich sich selbst ist und für jede reelle Zahl b als b = b ausgedrückt wird.
Im besonderen Fall der Gleichheit scheint diese Eigenschaft offensichtlich zu sein, in anderen Arten von Beziehungen zwischen Zahlen jedoch nicht. Mit anderen Worten, nicht jede reelle Zahlenbeziehung erfüllt diese Eigenschaft. Zum Beispiel ein solcher Fall der Beziehung "kleiner als" (<); ningún número es menor que sí mismo.
Die symmetrische Eigenschaft für Gleichheit besagt, dass wenn a = b, dann b = a. Die in den Variablen verwendete Reihenfolge spielt keine Rolle, sie wird durch die Gleichheitsrelation beibehalten.
Eine gewisse Analogie dieser Eigenschaft mit der kommutativen Eigenschaft kann im Falle der Addition beobachtet werden. Aufgrund dieser Eigenschaft ist es beispielsweise äquivalent, y = 4 oder 4 = y zu schreiben.
Die transitive Eigenschaft der Gleichheit besagt, dass wenn a = b und b = c, dann a = c. Zum Beispiel 2 + 7 = 9 und 9 = 6 + 3; daher haben wir durch die transitive Eigenschaft, dass 2 + 7 = 6 + 3.
Eine einfache Anwendung lautet wie folgt: Angenommen, Julian ist 14 Jahre alt und Mario ist genauso alt wie Rosa. Wenn Rosa genauso alt ist wie Julian, wie alt ist Mario??
Hinter diesem Szenario wird die transitive Eigenschaft zweimal verwendet. Mathematisch wird es so interpretiert: Sei "a" das Alter von Mario, "b" das Alter von Rosa und "c" das Alter von Julian. Es ist bekannt, dass b = c und c = 14 ist.
Durch die transitive Eigenschaft haben wir, dass b = 14; Das heißt, Rosa ist 14 Jahre alt. Da a = b und b = 14, haben wir bei erneuter Verwendung der transitiven Eigenschaft a = 14; Das heißt, Marios Alter ist ebenfalls 14 Jahre alt.
Die einheitliche Eigenschaft ist, dass die Gleichheit erhalten bleibt, wenn beide Seiten einer Gleichheit mit demselben Betrag addiert oder multipliziert werden. Wenn zum Beispiel 2 = 2 ist, dann ist 2 + 3 = 2 + 3, was klar ist, da 5 = 5. Diese Eigenschaft ist am nützlichsten, wenn Sie versuchen, eine Gleichung zu lösen.
Angenommen, Sie werden aufgefordert, die Gleichung x-2 = 1 zu lösen. Es ist zweckmäßig, sich daran zu erinnern, dass das Lösen einer Gleichung darin besteht, die betreffende Variable (oder Variablen) anhand einer bestimmten Zahl oder einer zuvor angegebenen Variablen explizit zu bestimmen..
Zurück zur Gleichung x-2 = 1 müssen Sie explizit herausfinden, wie viel x wert ist. Dazu muss die Variable gelöscht werden.
Es wurde fälschlicherweise gelehrt, dass in diesem Fall, da die Zahl 2 negativ ist, sie mit einem positiven Vorzeichen auf die andere Seite der Gleichheit übergeht. Aber es ist nicht richtig, es so zu sagen.
Grundsätzlich wenden Sie die einheitliche Eigenschaft an, wie wir weiter unten sehen werden. Die Idee ist, "x" zu löschen; das heißt, lassen Sie es auf einer Seite der Gleichung in Ruhe. Konventionell wird es normalerweise auf der linken Seite gelassen.
Zu diesem Zweck ist die zu "eliminierende" Zahl -2. Der Weg, dies zu tun, wäre das Addieren von 2, da -2 + 2 = 0 und x + 0 = 0. Um dies tun zu können, ohne die Gleichheit zu verändern, muss dieselbe Operation auf die andere Seite angewendet werden.
Dies ermöglicht es ihm, die einheitliche Eigenschaft zu realisieren: Da x-2 = 1 ist, sagt die einheitliche Eigenschaft, dass die einheitliche Eigenschaft nicht geändert wird, wenn die Zahl 2 auf beiden Seiten der Gleichheit hinzugefügt wird. Dann haben wir x-2 + 2 = 1 + 2, was gleichbedeutend ist mit x = 3. Damit wäre die Gleichung gelöst.
Wenn Sie die Gleichung (1/5) y-1 = 9 lösen möchten, können Sie die einheitliche Eigenschaft wie folgt verwenden:
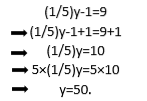
Allgemeiner können die folgenden Aussagen gemacht werden:
- Wenn a-b = c-b, dann ist a = c.
- Wenn x-b = y, dann ist x = y + b.
- Wenn (1 / a) z = b, dann ist z = a ×
- Wenn (1 / c) a = (1 / c) b, dann ist a = b.
Die Aufhebungseigenschaft ist ein besonderer Fall der einheitlichen Eigenschaft, wobei insbesondere der Fall der Subtraktion und Division berücksichtigt wird (die im Grunde auch der Addition und Multiplikation entsprechen). Diese Eigenschaft behandelt diesen Fall separat.
Wenn zum Beispiel 7 + 2 = 9 ist, dann ist 7 = 9-2. Oder wenn 2y = 6, dann ist y = 3 (auf beiden Seiten durch zwei geteilt).
Analog zum vorherigen Fall können durch die Stornierungseigenschaft die folgenden Aussagen getroffen werden:
- Wenn a + b = c + b, dann ist a = c.
- Wenn x + b = y, dann ist x = y-b.
- Wenn az = b, dann ist z = b / a.
- Wenn ca = cb, dann ist a = b.
Wenn wir den Wert eines mathematischen Objekts kennen, gibt die Substitutionseigenschaft an, dass dieser Wert in einer beliebigen Gleichung oder einem beliebigen Ausdruck eingesetzt werden kann. Wenn zum Beispiel b = 5 und a = bx ist, dann haben wir durch Ersetzen des Wertes von "b" in der zweiten Gleichheit a = 5x.
Ein anderes Beispiel ist das folgende: Wenn "m" "n" teilt und auch "n" "m" teilt, muss es m = n haben.
In der Tat bedeutet die Aussage, dass "m" "n" teilt (oder äquivalent, dass "m" ein Teiler von "n" ist), dass die Division m ÷ n genau ist; Das heißt, das Teilen von "m" durch "n" ergibt eine ganze Zahl, keine Dezimalzahl. Dies kann ausgedrückt werden, indem gesagt wird, dass es eine ganze Zahl "k" gibt, so dass m = k × n ist.
Da "n" auch "m" teilt, existiert eine ganze Zahl "p", so dass n = p × m ist. Aufgrund der Substitutionseigenschaft haben wir n = p × k × n, und dafür gibt es zwei Möglichkeiten: n = 0, in diesem Fall hätten wir die Identität 0 = 0; oder p × k = 1, daher die Identität n = n.
Angenommen, "n" ist ungleich Null. Dann ist notwendigerweise p × k = 1; daher ist p = 1 und k = 1. Wenn wir die Substitutionseigenschaft erneut verwenden, erhalten wir beim Ersetzen von k = 1 in der Gleichheit m = k × n (oder äquivalent p = 1 in n = p × m) schließlich m = n, was wir demonstrieren wollten.
Wie zuvor wurde festgestellt, dass eine Operation wie Addition, Multiplikation, Subtraktion oder Division in beiden Begriffen einer Gleichheit beibehalten wird, ebenso wie andere Operationen, die eine Gleichheit nicht ändern, angewendet werden können.
Der Schlüssel ist, es immer auf beiden Seiten der Gleichheit auszuführen und vorher sicherzustellen, dass die Operation ausgeführt werden kann. Dies ist der Fall von Empowerment; Das heißt, wenn beide Seiten einer Gleichung zur gleichen Potenz erhoben werden, haben wir immer noch eine Gleichheit.
Zum Beispiel, da 3 = 3, also 3zwei= 3zwei (9 = 9). Im Allgemeinen ist x gegeben, wenn eine ganze Zahl "n" gegeben ist, wenn x = yn= undn.
Dies ist ein besonderer Fall von Ermächtigung und wird angewendet, wenn die Potenz eine nicht ganzzahlige rationale Zahl ist, wie z. B. ½, die die Quadratwurzel darstellt. Diese Eigenschaft besagt, dass die Gleichheit erhalten bleibt, wenn dieselbe Wurzel (wann immer möglich) auf beide Seiten einer Gleichheit angewendet wird.
Im Gegensatz zum vorherigen Fall muss hier auf die Parität der anzuwendenden Wurzel geachtet werden, da bekanntlich die gerade Wurzel einer negativen Zahl nicht genau definiert ist.
Für den Fall, dass das Radikal gerade ist, gibt es kein Problem. Zum Beispiel, wenn x3= -8, obwohl es sich um eine Gleichheit handelt, können Sie beispielsweise nicht auf beide Seiten eine Quadratwurzel anwenden. Wenn Sie jedoch eine Kubikwurzel anwenden können (was noch praktischer ist, wenn Sie den Wert von x explizit kennen möchten), erhalten Sie x = -2.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.