
Lineare Programmierung, wofür es ist, Modelle, Einschränkungen, Anwendungen
Das Lineares Programmieren ist eine mathematische Methode zur Optimierung (Maximierung oder Minimierung nach Bedarf) einer Funktion, deren Variablen Einschränkungen unterliegen, solange die Funktion und die Einschränkungen linear von den Variablen abhängen.
Im Allgemeinen modelliert die zu optimierende Funktion eine praktische Situation, beispielsweise den Gewinn eines Herstellers, dessen Input, Arbeitskräfte oder Maschinen begrenzt sind.

Einer der einfachsten Fälle ist der einer zu maximierenden linearen Funktion, die nur von zwei Variablen abhängt, die aufgerufen werden Entscheidungsvariablen. Es kann von der Form sein:
Z = k1x + kzweiY.
Mit k1 und kzwei Konstante. Diese Funktion wird als bezeichnet Zielfunktion. Natürlich gibt es Situationen, die mehr als zwei Variablen für das Studium verdienen und komplexer sind:
Z = k1x1 + kzweixzwei + k3x3 +... .
Und die Einschränkungen werden auch mathematisch durch ein System von Gleichungen oder Ungleichungen modelliert, die gleichermaßen linear sind x und Y..
Die Menge der Lösungen dieses Systems wird aufgerufen machbare Lösungen oder machbare Punkte. Und unter den möglichen Punkten gibt es mindestens einen, der die Zielfunktion optimiert.
Die lineare Programmierung wurde vom amerikanischen Physiker und Mathematiker George Dantzig (1914-2005) und dem russischen Mathematiker und Ökonomen Leonid Kantorovich (1912-1986) kurz nach dem Zweiten Weltkrieg unabhängig voneinander entwickelt..
Die Fehlerbehebungsmethode, bekannt als Simplex-Methode Es ist die Idee von Dantzig, der für die US Air Force, die University of Berkeley und die Stanford University gearbeitet hat.

Artikelverzeichnis
- 1 Lineare Programmiermodelle
- 2 Modellbeispiel
- 3 Lösungsmethoden
- 3.1 - Grafische oder geometrische Methode
- 3.2 - Dantzigs Simplex-Methode
- 4 Anwendungen
- 5 Übungen gelöst
- 5.1 - Übung 1
- 5.2 - Übung 2
- 6 Referenzen
Lineare Programmiermodelle
Die Elemente, die erforderlich sind, um ein lineares Programmiermodell zu erstellen, das für eine praktische Situation geeignet ist, sind:
-Zielfunktion
-Entscheidungsvariablen
-Beschränkungen
In der Zielfunktion definieren Sie, was Sie erreichen möchten. Angenommen, Sie möchten Ihre Gewinne aus der Herstellung bestimmter Produkte maximieren. Dann wird die "Gewinn" -Funktion entsprechend dem Preis eingerichtet, zu dem die Produkte verkauft werden.
In mathematischen Begriffen kann diese Funktion mit der Summationsnotation abgekürzt ausgedrückt werden:
Z = ∑kich xich
In dieser Gleichung ist kich sind Koeffizienten und xich sind die Entscheidungsvariablen.
Die Entscheidungsvariablen sind die Elemente des Systems, deren Kontrolle vorhanden ist, und ihre Werte sind positive reelle Zahlen. In dem vorgeschlagenen Beispiel sind die Entscheidungsvariablen die Menge jedes Produkts, das hergestellt werden soll, um den maximalen Gewinn zu erzielen.
Schließlich haben wir die Einschränkungen, die lineare Gleichungen oder Ungleichungen in Bezug auf die Entscheidungsvariablen sind. Sie beschreiben die bekannten Einschränkungen des Problems und können beispielsweise die bei der Herstellung verfügbaren Rohstoffmengen sein..
Arten von Einschränkungen
Sie können M Anzahl von Einschränkungen haben, beginnend mit j = 1 bis um j = M.. Mathematisch gibt es drei Arten von Einschränkungen:
- ZUj = ∑ aij . xich
- B.j ≥ ∑ bij . xich
- C.j ≤ ∑ cij . xich
Die erste Einschränkung ist vom linearen Gleichungstyp und bedeutet, dass der Wert A.j, was bekannt ist, muss respektiert werden.
Die verbleibenden zwei Einschränkungen sind lineare Ungleichungen und dies bedeutet, dass die B-Wertej und Cj, bekannt, können sie respektiert oder überschritten werden, wenn das angezeigte Symbol ≥ (größer oder gleich) ist oder respektiert oder nicht überschritten wird, wenn das Symbol ≤ ist (kleiner oder gleich).
Modellbeispiel
Die Anwendungsbereiche sind sehr unterschiedlich und reichen von der Betriebswirtschaft bis zur Ernährung. Um die Methode zu verstehen, wird im Folgenden ein einfaches Modell einer praktischen Situation mit zwei Variablen vorgeschlagen..
Eine lokale Konditorei ist für zwei Spezialitäten bekannt: den Schwarzwälder Kuchen und den Sacripantina-Kuchen..
Bei der Zubereitung benötigen sie Eier und Zucker. Für den Schwarzwald benötigen Sie 9 Eier und 500 g Zucker, für das Sakripantin 8 Eier und 800 g Zucker. Die jeweiligen Verkaufspreise betragen 8 USD und 10 USD.
Das Problem ist: Wie viele Kuchen jeder Art muss das Gebäck machen, um seinen Gewinn zu maximieren, da es 10 Kilo Zucker und 144 Eier enthält?
Entscheidungsvariablen
Die Entscheidungsvariablen sind "x" und "y", die reale Werte annehmen:
-x: Anzahl der Schwarzwälder Kuchen
-und: die Kuchen vom Typ Sacripantina.
Beschränkungen
Die Einschränkungen ergeben sich aus der Tatsache, dass die Anzahl der Kuchen eine positive Menge ist und es nur begrenzte Mengen an Rohmaterial gibt, um sie zuzubereiten..
In mathematischer Form haben diese Einschränkungen daher die Form:
- x ≥ 0
- und ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8y ≤ 10
Die Bedingungen 1 und 2 bilden die Nicht-Negativitätsbedingung zuvor ausgesetzt, und alle Ungleichungen sind linear. In den Beschränkungen 3 und 4 sind die Werte angegeben, die nicht überschritten werden dürfen: 144 Eier und 10 kg Zucker.
Zielfunktion
Schließlich ist die Zielfunktion der Gewinn, der bei der Herstellung der Menge „x“ Schwarzwälder Kuchen plus der Menge „y“ Sakripantine erzielt wird. Es wird gebaut, indem der Preis mit der Menge der hergestellten Kuchen multipliziert und für jeden Typ addiert wird. Es ist eine lineare Funktion, die wir G (x, y) nennen werden:
G = 8x + 10y
Lösungsmethoden
Die verschiedenen Lösungsmethoden umfassen grafische Methoden, den Simplex-Algorithmus und die Innenpunktmethode, um nur einige zu nennen..
- Grafische oder geometrische Methode
Wenn Sie ein Problem mit zwei Variablen wie das im vorherigen Abschnitt haben, bestimmen die Einschränkungen einen polygonalen Bereich in der Ebene xy, Anruf machbare Region oder Region der Lebensfähigkeit.
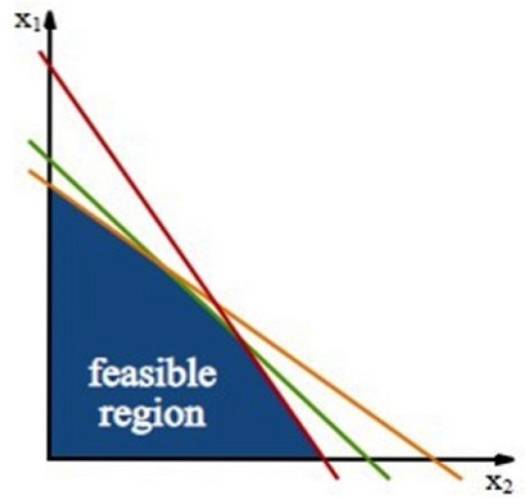
Diese Region wird mittels gebaut Restriktionslinien, Dies sind die Linien, die aus den Ungleichungen der Randbedingungen erhalten werden und nur mit dem Gleichheitszeichen arbeiten.
Bei der Bäckerei, die ihre Gewinne optimieren möchte, lauten die Beschränkungslinien:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8y = 10
Alle Punkte in der von diesen Linien eingeschlossenen Region sind mögliche Lösungen, daher gibt es unendlich viele davon. Außer in dem Fall, in dem sich herausstellt, dass der realisierbare Bereich leer ist, hat das aufgeworfene Problem keine Lösung.
Glücklicherweise ist für das Gebäckproblem die realisierbare Region nicht leer, wir haben sie unten.
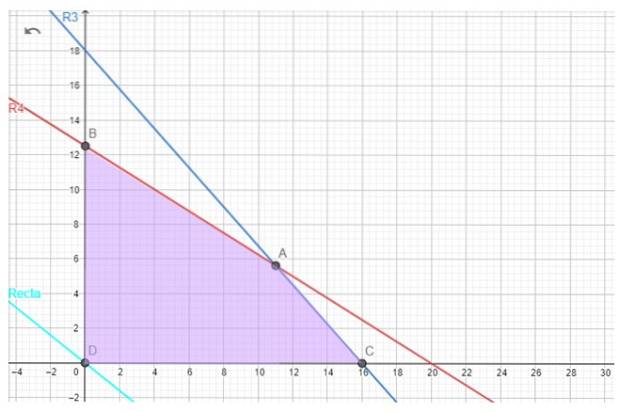
Die optimale Lösung, falls vorhanden, wird mit Hilfe der Zielfunktion gefunden. Wenn wir beispielsweise versuchen, die maximale Verstärkung G zu finden, haben wir die folgende Zeile, die aufgerufen wird Iso-Profit-Linie::
G = k1x + kzweiy → y = -k1x / kzwei + G / kzwei
Mit dieser Linie erhalten wir alle Paare (x, y), die eine gegebene Verstärkung G liefern, so dass es eine Linienfamilie gemäß dem Wert von G gibt, aber alle mit der gleichen Steigung -k1 / kzwei, Sie sind also parallele Linien.
Die optimale Lösung
Nun kann gezeigt werden, dass die optimale Lösung eines linearen Problems immer ein Extrempunkt oder Scheitelpunkt des realisierbaren Bereichs ist. Dann:
Die Lösungslinie ist die am weitesten vom Ursprung entfernte und hat mindestens einen Punkt gemeinsam mit der realisierbaren Region.
Wenn die Linie, die dem Ursprung am nächsten liegt, ein ganzes Segment mit der realisierbaren Region gemeinsam hat, wird gesagt, dass es unendlich viele Lösungen gibt. Dieser Fall tritt auf, wenn die Steigung der Iso-Profit-Linie gleich der einer der anderen Linien ist, die die Region begrenzen.
Für unser Gebäck sind die Eckpunkte A, B und C..
- Dantzigs Simplex-Methode
Die grafische oder geometrische Methode ist für zwei Variablen anwendbar. Es ist jedoch komplizierter, wenn drei Variablen vorhanden sind, und es ist unmöglich, sie für eine größere Anzahl von Variablen zu verwenden..
Bei Problemen mit mehr als zwei Variablen wird die Simplex-Methode, Das besteht aus einer Reihe von Algorithmen zur Optimierung der Zielfunktionen. Matrizen und einfache Arithmetik werden häufig verwendet, um die Berechnungen durchzuführen.
Die Simplex-Methode beginnt mit der Auswahl einer realisierbaren Lösung und der Überprüfung, ob diese optimal ist. Wenn dies der Fall ist, haben wir das Problem bereits gelöst. Wenn dies nicht der Fall ist, gehen wir weiter zu einer Lösung, die der Optimierung näher kommt. Wenn die Lösung vorhanden ist, findet der Algorithmus sie in wenigen Versuchen.
Anwendungen
Lineare und nichtlineare Programmierung werden in vielen Bereichen angewendet, um die besten Entscheidungen hinsichtlich Kostensenkung und Gewinnsteigerung zu treffen, was nicht immer monetär ist, da sie beispielsweise zeitlich gemessen werden können, wenn Sie die erforderliche Zeit minimieren möchten eine Reihe von Operationen durchzuführen.
Hier sind einige Felder:
-Im Marketing wird es verwendet, um die beste Kombination von Medien (soziale Netzwerke, Fernsehen, Presse und andere) zu finden, um für ein bestimmtes Produkt zu werben.
-Für die Zuweisung angemessener Aufgaben an das Personal eines Unternehmens oder einer Fabrik oder für Zeitpläne.
-Bei der Auswahl der nahrhaftesten Lebensmittel und zu den niedrigsten Kosten in der Vieh- und Geflügelindustrie.
Gelöste Übungen
- Übung 1
Lösen Sie das in den vorhergehenden Abschnitten erwähnte lineare Programmiermodell grafisch.
Lösung
Es ist erforderlich, den Wertesatz grafisch darzustellen, der durch das im Problem angegebene Einschränkungssystem bestimmt wird:
- x ≥ 0
- und ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8y ≤ 10
Der durch die Ungleichungen 1 und 2 gegebene Bereich entspricht dem ersten Quadranten der kartesischen Ebene. In Bezug auf die Ungleichungen 3 und 4 beginnen wir mit der Ermittlung der Restriktionslinien:
9x + 8y = 144
0,5 x + 0,8y = 10 → 5x + 8y = 100
Der realisierbare Bereich ist ein Viereck, dessen Eckpunkte die Punkte A, B, C und D sind.
Der minimale Gewinn ist 0, daher ist die Linie 8x + 10y = 0 die Untergrenze und die Iso-Profit-Linien haben eine Steigung von -8/10 = - 0,8.
Dieser Wert unterscheidet sich von den Steigungen der anderen Beschränkungslinien, und da der realisierbare Bereich begrenzt ist, existiert die eindeutige Lösung.
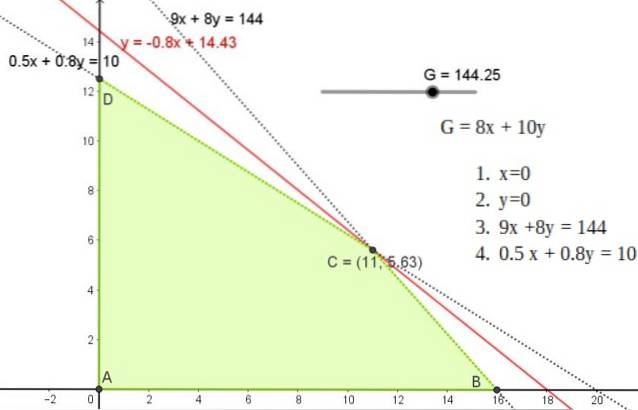
Diese Lösung entspricht einer Linie mit einer Steigung von -0,8, die durch einen der Punkte A, B oder C verläuft, deren Koordinaten sind:
A (11; 5,625)
B (0; 12,5)
C (16, 0)
Optimale Lösung
Wir berechnen den Wert von G für jeden dieser Punkte:
-(11; 5,625): G.ZU = 8 x 11 + 10 x 5,625 = 144,25
-(0; 12,5): G.B. = 8 x 0 + 10 x 12,5 = 125
-(16, 0): G.C. = 8 x 16 + 10 x 0 = 128
Der höchste Gewinn wird bei der Herstellung von 11 Schwarzwälder Kuchen und 5.625 Sakripantinkuchen erzielt. Diese Lösung entspricht der durch die Software gefundenen.
- Übung 2
Überprüfen Sie das Ergebnis der vorherigen Übung mithilfe der Solver-Funktion, die in den meisten Tabellenkalkulationen wie Excel oder LibreOffice Calc verfügbar ist und den Simplex-Algorithmus zur Optimierung in der linearen Programmierung enthält.
Lösung
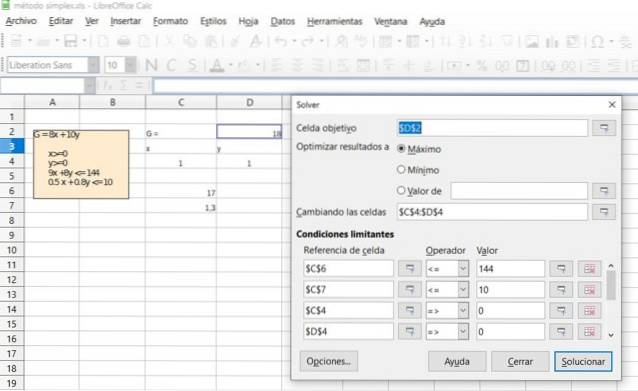
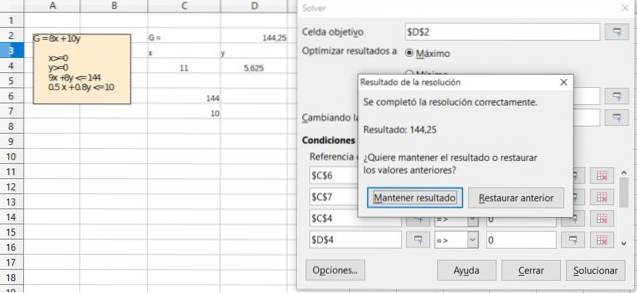
Verweise
- Brillant. Lineares Programmieren. Wiederhergestellt von: brillant.org.
- Eppen, G. 2000. Operations Research in Administrative Science. 5 .. Auflage. Prentice Halle.
- Haeussler, E. 1992. Mathematik für Management und Wirtschaft. 2 .. Auflage. Grupo Editorial Iberoamericana.
- Hiru.eus. Lineares Programmieren. Wiederhergestellt von: hiru.eus.
- Wikipedia. Lineares Programmieren. Wiederhergestellt von: es. wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.