
Produktübergreifende Eigenschaften, Anwendungen und Übungen
Das Kreuzprodukt oder Vektorprodukt Es ist eine Möglichkeit, zwei oder mehr Vektoren zu multiplizieren. Es gibt drei Möglichkeiten, Vektoren zu multiplizieren, aber keine davon ist eine Multiplikation im üblichen Sinne des Wortes. Eine dieser Formen ist als Vektorprodukt bekannt, wodurch wir einen dritten Vektor erhalten.
Das Kreuzprodukt, das auch als Kreuzprodukt oder Außenprodukt bezeichnet wird, weist unterschiedliche algebraische und geometrische Eigenschaften auf. Diese Eigenschaften sind besonders beim Studium der Physik sehr nützlich..

Artikelverzeichnis
- 1 Definition
- 2 Eigenschaften
- 2.1 Eigenschaft 1
- 2.2 Eigenschaft 2
- 2.3 Eigenschaft 3
- 2.4 Eigenschaft 4 (Dreipunktprodukt)
- 2.5 Eigenschaft 5 (Dreifachvektorprodukt)
- 2.6 Eigenschaft 6
- 2.7 Eigenschaft 7
- 2.8 Eigenschaft 8
- 3 Anwendungen
- 3.1 Berechnung des Volumens eines Parallelepipeds
- 4 Gelöste Übungen
- 4.1 Übung 1
- 4.2 Übung 2
- 5 Referenzen
Definition
Eine formale Definition des Vektorprodukts lautet wie folgt: Wenn A = (a1, a2, a3) und B = (b1, b2, b3) Vektoren sind, dann ist das Vektorprodukt von A und B, das wir als AxB bezeichnen werden, ist:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
Aufgrund der AxB-Notation wird es als "A cross B" gelesen..
Ein Beispiel für die Verwendung des äußeren Produkts ist, dass wenn A = (1, 2, 3) und B = (3, -2, 4) Vektoren sind, wir die Definition eines Vektorprodukts verwenden:
AxB = (1, 2, 3) x (3, -2, 4) = (2 · 4 - 3 · (- 2), 3 · 3 - 1 · 4, 1 · (- 2) - 2 · 3)
AxB = (8 + 6, 9 - 4, - 2 - 6) = (14, 5, - 8).
Eine andere Art, das Vektorprodukt auszudrücken, ist die Notation von Determinanten.
Die Berechnung einer Determinante zweiter Ordnung ist gegeben durch:
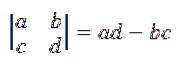
Daher kann die in der Definition angegebene Formel für das Kreuzprodukt wie folgt umgeschrieben werden:
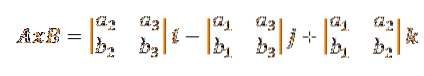
Dies wird normalerweise wie folgt zu einer Determinante dritter Ordnung vereinfacht:
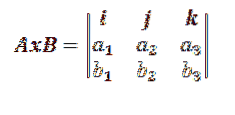
Wobei i, j, k die Vektoren darstellen, die die Basis von R bilden3.
Mit dieser Art, das Kreuzprodukt auszudrücken, kann das vorherige Beispiel wie folgt umgeschrieben werden:
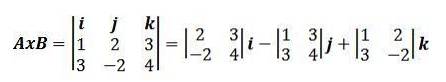
Eigenschaften
Einige Eigenschaften, die das Vektorprodukt besitzt, sind die folgenden:
Eigenschaft 1
Wenn A ein Vektor in R ist3, wir müssen:
- AxA = 0
- Ax0 = 0
- 0xA = 0
Diese Eigenschaften lassen sich nur anhand der Definition leicht überprüfen. Wenn A = (a1, a2, a3) haben wir:
AxA = (a2a3 - a3a2, a3a1 - a1a3, a1a2 - a2a1) = (0, 0, 0) = 0.
Ax0 = (a2 * 0 - a3 * 0, a3 * 0 - a1 * 0, a1 * 0 - a2 * 0) = (0, 0, 0) = 0.
Wenn i, j, k die Einheitsbasis von R darstellen3, wir können sie wie folgt schreiben:
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
Wir haben also, dass die folgenden Eigenschaften wahr sind:
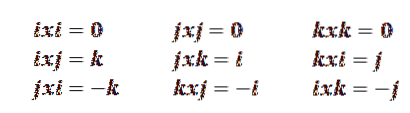
In der Regel wird häufig der folgende Kreis verwendet, um sich an diese Eigenschaften zu erinnern:
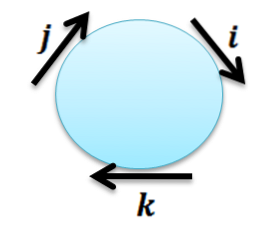
Dort müssen wir beachten, dass jeder Vektor mit sich selbst als Ergebnis den Vektor 0 ergibt und der Rest der Produkte mit der folgenden Regel erhalten werden kann:
Das Kreuzprodukt zweier aufeinanderfolgender Vektoren im Uhrzeigersinn ergibt den nächsten Vektor; und wenn gegen den Uhrzeigersinn betrachtet wird, ist das Ergebnis der folgende Vektor mit negativem Vorzeichen.
Dank dieser Eigenschaften können wir sehen, dass das Vektorprodukt nicht kommutativ ist; Beachten Sie zum Beispiel, dass i x j ≠ j x i ist. Die folgende Eigenschaft zeigt uns, wie AxB und BxA im Allgemeinen zusammenhängen.
Eigenschaft 2
Wenn A und B Vektoren von R sind3, wir müssen:
AxB = - (BxA).
Demonstration
Wenn A = (a1, a2, a3) und B = (b1, b2, b3), haben wir per Definition des externen Produkts:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
= (- 1) (a3b2 - a2b3, a1b3 - a3b1, a2b1 - a1b2)
= (- 1) (BxA).
Wir können auch sehen, dass dieses Produkt nicht mit dem folgenden Beispiel assoziiert ist:
ix (ixj) = ixk = - j, aber (ixi) xj = 0xj = 0
Daraus können wir sehen, dass:
ix (ixj) ≠ (ixi) xj
Eigenschaft 3
Wenn A, B, C Vektoren von R sind3 und r ist eine reelle Zahl, das Folgende ist wahr:
- Ax (B + C) = AxB + AxC
- r (AxB) = (rA) xB = Ax (rB)
Dank dieser Eigenschaften können wir das Vektorprodukt nach den Gesetzen der Algebra berechnen, sofern die Reihenfolge eingehalten wird. Beispielsweise:
Wenn A = (1, 2, 3) und B = (3, -2, 4), können wir sie basierend auf der kanonischen Basis von R umschreiben3.
Somit ist A = i + 2j + 3k und B = 3i - 2j + 4k. Wenden Sie dann die vorherigen Eigenschaften an:
AxB = (i + 2j + 3k) x (3i - 2j + 4k)
= 3 (ixi) - 2 (ixj) + 4 (ixk) + 6 (jxi) - 4 (jxj) + 8 (jxk) + 9 (kxi) - 6 (kxj) +12 (kxk)
= 3 (0) - 2 (k) + 4 (- j) + 6 (- k) - 4 (0) + 8 (i) + 9 (j) - 6 (- i) + 12 (0)
= - 2k - 4j - 6k + 8i + 9j + 6i = 14i + 5j - 4k
= (14, 5, - 8).
Eigenschaft 4 (Dreifachpunktprodukt)
Wie eingangs erwähnt, gibt es neben dem Vektorprodukt noch andere Möglichkeiten, Vektoren zu multiplizieren. Eine dieser Möglichkeiten ist das Skalarprodukt oder das innere Produkt, das als A ∙ B bezeichnet wird und dessen Definition lautet:
Wenn A = (a1, a2, a3) und B = (b1, b2, b3), dann ist A ∙ B = a1b1 + a2b2 + a3b3
Die Eigenschaft, die beide Produkte betrifft, ist als dreifach skalares Produkt bekannt.
Wenn A, B und C Vektoren von R sind3, dann ist A ∙ BxC = AxB ∙ C.
Als Beispiel sehen wir, dass bei A = (1, 1, - 2), B = (- 3, 4, 2) und C = (- 5, 1, - 4) diese Eigenschaft erfüllt ist.
BxC = - 3k - 12j + 20k - 16i - 10j - 2i = - 18i - 22j + 17k
A ∙ BxC = (1, 1, - 2) ∙ (- 18, - 22, 17) = (1) (- 18) + (1) (- 22) + (- 2) (17) = - 74
Andererseits:
AxB = 4k - 2j + 3k + 2i + 6j + 8i = 10i + 4j + 7k
AxB ≤ C = (10, 4, 7) ≤ (- 5, 1, - 4) = (10) (- 5) + (4) (1) + (7) (- 4) = - 74
Ein weiteres Dreifachprodukt ist Ax (BxC), das als Dreifachvektorprodukt bekannt ist..
Eigenschaft 5 (Dreifachvektorprodukt)
Wenn A, B und C Vektoren von R sind3, dann:
Ax (BxC) = (A ∙ C) B - (A ∙ B) C.
Als Beispiel sehen wir, dass bei A = (1, 1, - 2), B = (- 3, 4, 2) und C = (- 5, 1, - 4) diese Eigenschaft erfüllt ist.
Aus dem vorherigen Beispiel wissen wir, dass BxC = (- 18, - 22, 17). Berechnen wir Axe (BxC):
Axe (BxC) = - 22k - 17j + 18k + 17i + 36j - 44i = - 27i + 19j - 4k
Auf der anderen Seite müssen wir:
A ∙ C = (1, 1, - 2) ∙ (- 5, 1, - 4) = (1) (- 5) + (1) (1) + (- 2) (- 4) = - 5 + 1 + 8 = 4
A ∙ B = (1, 1, - 2) ∙ (- 3, 4, 2) = (1) (- 3) + (1) (4) + (- 2) (2) = - 3 + 4 - 4 = - 3
Wir müssen also:
(A ∙ C) B - (A ∙ B) C = 4 (- 3, 4, 2) + 3 (- 5, 1, - 4) = (- 12, 16, 8) + (- 15, 3, - 12) = (- 27,19, -4)
Eigentum 6
Dies ist eine der geometrischen Eigenschaften von Vektoren. Wenn A und B zwei Vektoren in R sind3 und ϴ ist der Winkel, der zwischen diesen gebildet wird, dann:
|| AxB || = || A |||| B || sin (ϴ), wobei || ∙ || bezeichnet den Modul oder die Größe eines Vektors.
Die geometrische Interpretation dieser Eigenschaft lautet wie folgt:
Sei A = PR und B = PQ. Dann ist der durch die Vektoren A und B gebildete Winkel der Winkel P des Dreiecks RQP, wie in der folgenden Figur gezeigt.
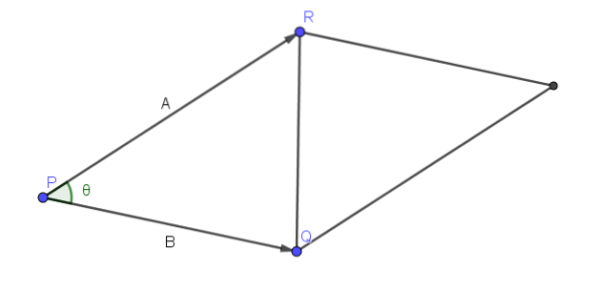
Daher ist die Fläche des Parallelogramms, die PR und PQ als benachbarte Seiten hat, || A |||| B || sin (ϴ), da wir || A || als Basis nehmen können und seine Höhe ist gegeben durch || B || sin (ϴ).
Daraus können wir schließen, dass || AxB || ist die Fläche des Parallelogramms.
Beispiel
Ausgehend von den folgenden Eckpunkten eines Vierecks P (1, -2,3) zeigen Q (4, 3, -1), R (2, 2,1) und S (5,7, -3), dass das Viereck ist ein Parallelogramm und finde seine Fläche.
Dazu bestimmen wir zunächst die Vektoren, die die Richtung der Seiten des Vierecks bestimmen. Das ist:
A = PQ = (1 - 4, 3 + 2, - 1 - 3) = (3, 5, - 4)
B = PR = (2 - 1, 2 + 2, 1 - 3) = (1, 4, - 2)
C = RS = (5 - 2, 7 - 2, - 3 - 1) = (3, 5, - 4)
D = QS = (5 - 4, 7 - 3, - 3 + 1) = (1, 4, - 2)
Wie wir sehen können, haben A und C den gleichen Direktorvektor, also haben wir, dass beide parallel sind; Das gleiche passiert mit B und D. Daher schließen wir, dass PQRS ein Parallelogramm ist.
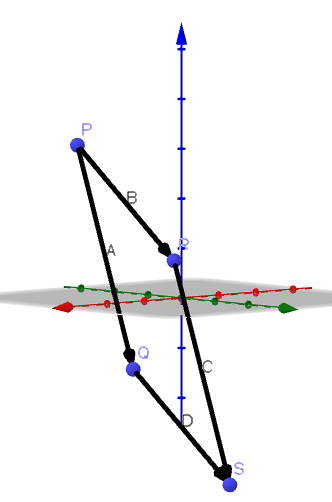
Um die Fläche dieses Parallelogramms zu erhalten, berechnen wir BxA:
BxA = (i + 4j - 2k) x (3i + 5j - 4k)
= 5k + 4j - 12k - 16i - 6j + 10i
= - 6i - 2j - 7k.
Daher ist die quadratische Fläche:
|| BxA ||zwei = (- 6)zwei + (- zwei)zwei + (- 7)zwei = 36 + 4 + 49 = 89.
Es kann geschlossen werden, dass der Parallelogrammbereich die Quadratwurzel von 89 ist.
Eigentum 7
Zwei Vektoren A und B sind in R parallel3 genau dann, wenn AxB = 0 ist
Demonstration
Es ist klar, dass wenn A oder B der Nullvektor sind, AxB = 0 ist. Da der Nullvektor parallel zu jedem anderen Vektor ist, ist die Eigenschaft gültig.
Wenn keiner der beiden Vektoren der Nullvektor ist, haben wir, dass sich ihre Größen von Null unterscheiden; das heißt, beide || A || ≠ 0 als || B || ≠ 0, also haben wir || AxB || = 0 genau dann, wenn sin (ϴ) = 0 ist, und dies geschieht genau dann, wenn ϴ = π oder ϴ = 0 ist.
Daher können wir AxB = 0 genau dann schließen, wenn ϴ = π oder ϴ = 0 ist, was nur dann geschieht, wenn beide Vektoren parallel zueinander sind.
Eigentum 8
Wenn A und B zwei Vektoren in R sind3, dann ist AxB senkrecht zu A und B..
Demonstration
Denken Sie für diesen Beweis daran, dass zwei Vektoren senkrecht sind, wenn A ∙ B gleich Null ist. Darüber hinaus wissen wir, dass:
A ∙ AxB = AxA ∙ B, aber AxA ist gleich 0. Daher haben wir:
A ∙ AxB = 0 ∙ B = 0.
Daraus können wir schließen, dass A und AxB senkrecht zueinander stehen. Ebenso müssen wir:
AxB ≤ B = A ≤ BxB.
Da BxB = 0 ist, haben wir:
AxB ≤ B = A ≤ 0 = 0.
Daher stehen AxB und B senkrecht zueinander und damit wird die Eigenschaft demonstriert. Dies ist sehr nützlich, da wir damit die Gleichung einer Ebene bestimmen können.
Beispiel 1
Erhalten Sie eine Gleichung der Ebene, die durch die Punkte P (1, 3, 2), Q (3, - 2, 2) und R (2, 1, 3) verläuft..
Es sei A = QR = (2 - 3,1 + 2, 3 - 2) und B = PR = (2 - 1,1 - 3, 3 - 2). Dann ist A = - i + 3j + k und B = i - 2j + k. Um die durch diese drei Punkte gebildete Ebene zu finden, reicht es aus, einen Vektor zu finden, der normal zur Ebene ist, nämlich AxB.
AxB = (- i + 3j + k) x (i - 2j + k) = 5i + 2j - k.
Mit diesem Vektor und unter Verwendung des Punktes P (1, 3, 2) können wir die Gleichung der Ebene wie folgt bestimmen:
(5, 2, - 1) ∙ (x - 1, y - 3, z - 2) = 5 (x - 1) + 2 (y - 3) - (z - 2) = 0
Wir haben also, dass die Gleichung der Ebene 5x + 2y - z - 9 = 0 ist.
Beispiel 2
Finden Sie die Gleichung der Ebene, die den Punkt P (4, 0, - 2) enthält und die senkrecht zu jeder der Ebenen x - y + z = 0 und 2x + y - 4z - 5 = 0 ist .
Wenn wir wissen, dass ein Normalenvektor zu einer Ebene ax + durch + cz + d = 0 (a, b, c) ist, haben wir, dass (1, -1,1) ein Normalenvektor von x - y + z = 0 y ist (2,1, - 4) ist ein Normalvektor von 2x + y - 4z - 5 = 0.
Daher muss ein Normalenvektor zur gesuchten Ebene senkrecht zu (1, -1,1) und zu (2, 1, - 4) sein. Der Vektor ist:
(1, -1,1) x (2,1, - 4) = 3i + 6j + 3k.
Dann haben wir, dass die gesuchte Ebene diejenige ist, die den Punkt P (4,0, - 2) enthält und den Vektor (3,6,3) als Normalenvektor hat.
3 (x - 4) + 6 (y - 0) + 3 (z + 2) = 0
x + 2y + z - 2 = 0.
Anwendungen
Volumenberechnung eines Parallelepipeds
Eine Anwendung mit dem dreifach skalaren Produkt besteht darin, das Volumen eines Parallelepipeds berechnen zu können, dessen Kanten durch die Vektoren A, B und C gegeben sind, wie in der Abbildung gezeigt:
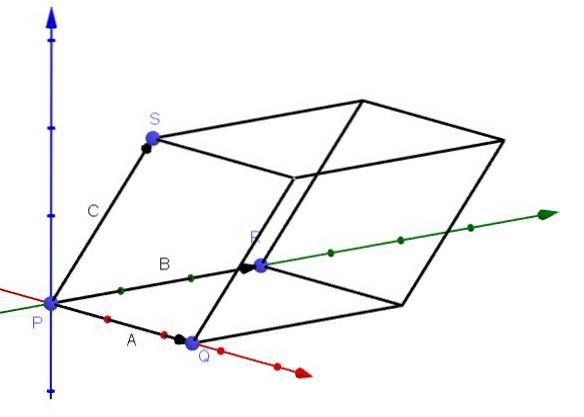
Wir können diese Anwendung folgendermaßen ableiten: Wie wir zuvor gesagt haben, ist der Vektor AxB ein Vektor, der normal zur Ebene von A und B ist. Wir haben auch, dass der Vektor - (AxB) ein anderer Vektor ist, der normal zu dieser Ebene ist.
Wir wählen den Normalenvektor, der mit dem Vektor C den kleinsten Winkel bildet; Sei AxB ohne Verlust der Allgemeinheit der Vektor, dessen Winkel mit C der kleinste ist.
Wir haben, dass sowohl AxB als auch C den gleichen Ausgangspunkt haben. Darüber hinaus wissen wir, dass der Bereich des Parallelogramms, der die Basis des Parallelepipeds bildet, || AxB || ist. Wenn also die Höhe des Parallelepipeds durch h gegeben ist, haben wir, dass sein Volumen sein wird:
V = || AxB || h.
Betrachten wir andererseits das Skalarprodukt zwischen AxB und C, das wie folgt beschrieben werden kann:
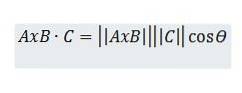
Durch trigonometrische Eigenschaften haben wir jedoch h = || C || cos (ϴ), also haben wir:
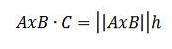
Auf diese Weise haben wir das:
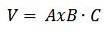
Im Allgemeinen haben wir, dass das Volumen eines Parallelepipeds durch den Absolutwert des dreifach skalaren Produkts AxB ∙ C gegeben ist.
Gelöste Übungen
Übung 1
Bei den Punkten P = (5, 4, 5), Q = (4, 10, 6), R = (1, 8, 7) und S = (2, 6, 9) bilden diese Punkte ein Parallelepiped, dessen Kanten Sie sind PQ, PR und PS. Bestimmen Sie das Volumen des Parallelepipeds.
Lösung
Wenn wir nehmen:
- A = PQ = (-1, 6, 1)
- B = PR = (-4, 4, 2)
- C = PS = (-3, 2, 2)
Unter Verwendung der Eigenschaft des dreifach skalaren Produkts haben wir:
AxB = (-1, 6, 1) x (-4, 4, 2) = (8, -2, 20).
AxB ≤ C = (8, -2, 20) ≤ (-3, 2, 2) = -24 -4 +80 = 52.
Daher haben wir, dass das Volumen des Parallelepipeds 52 beträgt.
Übung 2
Bestimmen Sie das Volumen eines Parallelepipeds, dessen Kanten durch A = PQ, B = PR und C = PS gegeben sind, wobei die Punkte P, Q, R und S (1, 3, 4), (3, 5, 3) sind. (2, 1, 6) bzw. (2, 2, 5).
Lösung
Zuerst haben wir A = (2, 2, -1), B = (1, -2, 2), C = (1, -1, 1).
Wir berechnen AxB = (2, 2, -1) x (1, -2, 2) = (2, -5, -6).
Dann berechnen wir AxB ∙ C:
AxB ≤ C = (2, -5, -6) ≤ (1, -1, 1) = 2 + 5 - 6 = 1.
Wir schließen daraus, dass das Volumen des Parallelepipeds 1 Kubikeinheit beträgt.
Verweise
- Leithold, L. (1992). Die Berechnung mit analytischer Geometrie. HARLA, S.A..
- Resnick, R., Halliday, D. & Krane, K. (2001). Physics Vol. 1. Mexiko: Kontinental.
- Saenz, J. (s.f.). Vektorrechnung 1ed. Hypotenuse.
- Spiegel, M. R. (2011). Vektoranalyse 2ed. Mc Graw Hill.
- Zill, D. G. & Wright, W. (2011). Berechnung mehrerer Variablen 4ed. Mc Graw Hill.

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.