
Polytrope Prozesseigenschaften, Anwendungen und Beispiele
EIN polytropischer Prozess ist ein thermodynamischer Prozess, der auftritt, wenn die Beziehung zwischen dem Druck P. und die Lautstärke V. gegeben durch P.V.n es bleibt konstant. Der Exponent n ist eine reelle Zahl, im Allgemeinen zwischen Null und Unendlich, kann aber in einigen Fällen negativ sein.
Der Wert von n erhält den Namen von Polytropie-Index und es ist wichtig hervorzuheben, dass während eines polytropischen thermodynamischen Prozesses der Index einen festen Wert beibehalten muss, sonst wird der Prozess nicht als polytrop angesehen.

Artikelverzeichnis
- 1 Eigenschaften polytropischer Prozesse
- 2 Anwendungen
- 2.1 Arbeiten an polytropischen Prozessen für verschiedene Werte von n
- 3 Beispiele für polytrope Prozesse
- 3.1 - Beispiel 1
- 3.2 - Beispiel 2
- 4 Referenzen
Eigenschaften polytropischer Prozesse
Einige charakteristische Fälle von polytropischen Prozessen sind:
- Der isotherme Prozess (bei konstanter Temperatur T), bei dem der Exponent n = 1 ist.
- Ein isobarer Prozess (bei konstantem Druck P), in diesem Fall n = 0.
- Der isochore Prozess (bei konstantem Volumen V), für den n = + ∞ ist.
- Adiabatische Prozesse (bei konstanter S-Entropie), bei denen der Exponent n = γ ist, wobei γ die adiabatische Konstante ist. Diese Konstante ist der Quotient zwischen der Wärmekapazität bei konstantem Druck Cp geteilt durch die Wärmekapazität bei konstantem Volumen Cv:
γ = Cp / Cv
- Jeder andere thermodynamische Prozess, der nicht zu den vorherigen Fällen gehört. aber das stimmt P.V.n = ctte mit realem und konstantem Polytropenindex n Es wird auch ein polytropischer Prozess sein.
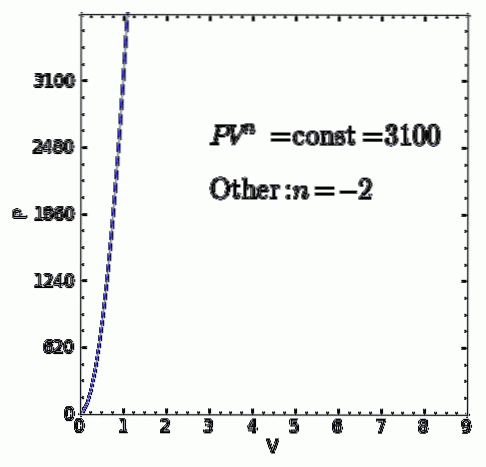
Anwendungen
Eine der Hauptanwendungen der polytropischen Gleichung besteht darin, die Arbeit eines geschlossenen thermodynamischen Systems zu berechnen, wenn es quasistatisch, dh nach einer Abfolge von Gleichgewichtszuständen, von einem Anfangszustand in einen Endzustand übergeht.
Arbeiten Sie an polytropischen Prozessen für verschiedene Werte von n
Für n ≠ 1
Die mechanische Arbeit W, die von einem geschlossenen thermodynamischen System ausgeführt wird, wird durch den Ausdruck berechnet:
W = ∫P.dV
Wobei P der Druck und V das Volumen ist.
Wie bei einem polytropischen Prozess ist die Beziehung zwischen Druck und Volumen:
P.V. n = konstant = C.
Auflösen nach P aus dem vorherigen Ausdruck, um es im Arbeitsausdruck zu ersetzen:
P = C /V. n
Wir haben die mechanische Arbeit während eines polytropischen Prozesses ausgeführt, der in einem Anfangszustand 1 beginnt und in einem Endzustand 2 endet. All dies erscheint im folgenden Ausdruck:


C = P.1 V.1n = P.zwei V.zwein
Durch Ersetzen des Wertes der Konstante im Arbeitsausdruck erhalten wir:
W = (P.zwei V.zwei - P.1 V.1) / (1-n)
Für den Fall, dass der Arbeitsstoff als ideales Gas modelliert werden kann, haben wir folgende Zustandsgleichung:
P.V. = m.R.T.
Dabei ist m die Molzahl des idealen Gases und R die universelle Gaskonstante.
Für ein ideales Gas, das einem polytropischen Prozess mit einem von der Einheit verschiedenen Polytropieindex folgt und aus einem Zustand mit der Anfangstemperatur T übergeht1 in einen anderen Zustand mit der Temperatur T.zwei Wir haben, dass die geleistete Arbeit durch die folgende Formel gegeben ist:
W = m R (T.zwei - T.1) / (1-n)
Für n → ∞
Nach der Formel für die im vorherigen Abschnitt erhaltene Arbeit haben wir, dass die Arbeit eines polytropischen Prozesses mit n = ∞ null ist, weil der Ausdruck der Arbeit durch unendlich geteilt wird und das Ergebnis daher gegen Null tendiert.
Ein anderer Weg, um zu diesem Ergebnis zu gelangen, ist aus der Beziehung P.1 V.1n = P.zwei V.zwein, die wie folgt umgeschrieben werden kann:
(P.1/ P.zwei) = (V.zwei/ V1)n
Wenn wir in jedem Mitglied die n-te Wurzel ziehen, erhalten wir:
(V.zwei/ V1) = (P.1/ P.zwei)(1 / n)
Für den Fall, dass n → ∞ ist, haben wir (V.zwei/ V1) = 1, was bedeutet, dass:
V.zwei = V.1
Das heißt, das Volumen ändert sich in einem polytropischen Prozess mit n → ∞ nicht. Daher beträgt die Volumendifferenz dV im Integral der mechanischen Arbeit 0. Diese Arten von polytropischen Prozessen werden auch als Prozesse bezeichnet isochorisch, oder Prozesse mit konstantem Volumen.
Für n = 1
Wieder haben wir den Ausdruck der Ausdruck für Arbeit:
W = ∫P dV
Bei einem polytropischen Prozess mit n = 1 beträgt die Beziehung zwischen Druck und Volumen:
P V = konstant = C.
Durch Auflösen nach P aus dem vorherigen Ausdruck und Ersetzen haben wir die Arbeit erledigt, um vom Anfangszustand 1 zum Endzustand 2 zu gelangen:

Nämlich:
W = C ln (V.zwei/ V.1).
Da der Anfangs- und der Endzustand gut bestimmt sind, wird auch der Ctte gut bestimmt. Nämlich:
C = P.1 V.1 = P.zwei V.zwei
Schließlich haben wir die folgenden nützlichen Ausdrücke, um die mechanische Arbeit eines polytropischen geschlossenen Systems zu finden, in dem n = 1 ist.
W = P.1 V.1 ln (V.zwei/ V.1) = P.zwei V.zwei ln (V.zwei/ V.1)
Wenn der Arbeitsstoff besteht aus m Mol ideales Gas, dann kann die ideale Gaszustandsgleichung angewendet werden: P V = m.R.T..
In diesem Fall als P.V.1 = ctte, wir haben, dass ein polytropischer Prozess mit n = 1 ein Prozess bei konstanter Temperatur T (isotherm) ist, so dass die folgenden Ausdrücke für die Arbeit erhalten werden können:
W = m R T.1 ln (V.zwei/ V.1) = m R T.zwei ln (V.zwei/ V.1)

Beispiele für polytrope Prozesse
- Beispiel 1
Angenommen, ein Zylinder mit einem beweglichen Kolben ist mit einem Kilogramm Luft gefüllt. Anfangs nimmt die Luft ein Volumen V ein1= 0,2 m3 bei einem Druck P.1= 400 kPa. Ein polytropischer Prozess wird mit n = γ = 1,4 verfolgt, dessen Endzustand den Druck P hatzwei = 100 kPa. Bestimmen Sie die Arbeit der Luft am Kolben.
Lösung
Wenn der Polytropieindex gleich der adiabatischen Konstante ist, gibt es einen Prozess, bei dem der Arbeitsstoff (Luft) keine Wärme mit der Umgebung austauscht und sich daher die Entropie nicht ändert..
Für Luft, ein zweiatomiges ideales Gas, haben wir:
γ = Cp / Cv, mit Cp = (7/2) R und Cv = (5/2) R.
Dann:
γ = 7/5 = 1,4
Unter Verwendung des Ausdrucks des polytropischen Prozesses kann das endgültige Luftvolumen bestimmt werden:
V.zwei = [(P.zwei V.11.4) / P.zwei]](1 / 1.4) = 0,54 m3.
Jetzt haben wir die Bedingungen, um die Formel für Arbeiten anzuwenden, die in einem polytropischen Prozess für n ≠ 1 durchgeführt wurden, wie oben erhalten:
W = (P.zwei V.zwei - P1 V1) / (1-n)
Ersetzen Sie die entsprechenden Werte, die wir haben:
W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3) / (1 - 1,4) = 65,4 kJ
- Beispiel 2
Es sei der gleiche Zylinder aus Beispiel 1 mit einem beweglichen Kolben angenommen, der mit einem Kilogramm Luft gefüllt ist. Die Luft nimmt zunächst ein Volumen V1 = 0,2 m ein3 bei einem Druck P1 = 400 kPa. Im Gegensatz zum vorherigen Fall dehnt sich die Luft jedoch isotherm aus, um einen Enddruck P2 = 100 kPa zu erreichen. Bestimmen Sie die Arbeit der Luft am Kolben.
Lösung
Wie bereits erwähnt, handelt es sich bei isothermen Prozessen um polytrope Prozesse mit dem Index n = 1. Es ist also richtig, dass:
P1 V1 = P2 V2
Auf diese Weise kann das Endvolumen leicht abgezogen werden, um Folgendes zu erhalten:
V2 = 0,8 m3
Dann haben wir unter Verwendung des zuvor für den Fall n = 1 erhaltenen Arbeitsausdrucks, dass die Arbeit, die die Luft auf dem Kolben in diesem Prozess leistet, ist:
W = P1 V1 ln (V2 / V1) = 400000 Pa × 0,2 m3 ln (0,8 / 0,2) = 110,9 kJ.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Cengel, Y. 2012. Thermodynamik. 7. Auflage. Mcgraw Hügel.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 4. Flüssigkeiten und Thermodynamik. Herausgegeben von Douglas Figueroa (USB).
- López, C. Der erste Hauptsatz der Thermodynamik. Wiederhergestellt von: kulturacientifica.com.
- Knight, R. 2017. Physik für Wissenschaftler und Ingenieure: ein strategischer Ansatz. Pearson.
- Serway, R., Vulle, C. 2011. Grundlagen der Physik. 9. Aufl. Lernen einbinden.
- Sevilla Universität. Thermische Maschinen. Wiederhergestellt von: laplace.us.es.
- Wikiwand. Polytropischer Prozess. Wiederhergestellt von: wikiwand.com.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.