
Pascals Prinzip Geschichte, Anwendungen, Beispiele
Das Pascals Prinzip, oder Pascals Gesetz legt fest, dass eine Änderung des Drucks einer Flüssigkeit, die in einem ihrer Punkte eingeschlossen ist, ohne Änderung auf alle anderen Punkte innerhalb der Flüssigkeit übertragen wird.
Dieses Prinzip wurde vom französischen Wissenschaftler Blaise Pascal (1623 - 1662) entdeckt. Aufgrund der Bedeutung der Beiträge von Pascal zur Wissenschaft wurde ihm zu Ehren die Druckeinheit im Internationalen System benannt..

Da Druck als das Verhältnis der Kraft senkrecht zu einer Oberfläche und ihrer Fläche definiert ist, entspricht 1 Pascal (Pa) 1 Newton / mzwei.
Artikelverzeichnis
- 1 Geschichte
- 2 Erklärung des Pascalschen Prinzips
- 2.1 Das Verhältnis zwischen Druck und Tiefe
- 3 Anwendungen
- 3.1 Die hydraulische Presse
- 4 Beispiele
- 4.1 Hydraulische Bremsen
- 4.2 Mechanischer Vorteil der hydraulischen Presse
- 5 Übung gelöst
- 6 Referenzen
Geschichte
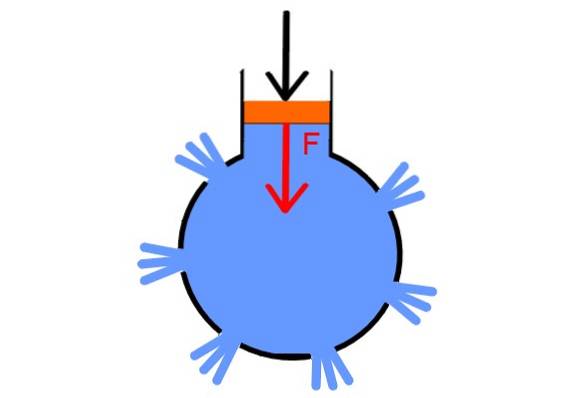
Um sein Prinzip zu testen, entwickelte Pascal einen ziemlich überzeugenden Beweis. Er nahm eine hohle Kugel und bohrte an mehreren Stellen, steckte Stecker in alle Löcher außer einem, durch die er sie mit Wasser füllte. Darin platzierte er eine Spritze mit einem Kolben.
Durch ausreichendes Erhöhen des Drucks im Kolben werden die Stopfen gleichzeitig freigegeben, da der Druck gleichmäßig auf alle Punkte der Flüssigkeit und in alle Richtungen übertragen wird, wodurch das Pascalsche Gesetz demonstriert wird.
Blaise Pascal hatte ein kurzes Leben, das von Krankheit geprägt war. Der unglaubliche Umfang seines Geistes veranlasste ihn, verschiedene Aspekte der Natur und Philosophie zu untersuchen. Seine Beiträge beschränkten sich nicht nur auf die Untersuchung des Verhaltens von Flüssigkeiten, Pascal war auch ein Pionier des Rechnens.
Und genau im Alter von 19 Jahren schuf Pascal einen mechanischen Taschenrechner, den sein Vater für seine Arbeit im französischen Steuersystem verwenden konnte: den pascaline.
Zusammen mit seinem Freund und Kollegen, dem großen Mathematiker Pierre de Fermat, formten sie auch die Wahrscheinlichkeitstheorie, die in Physik und Statistik unverzichtbar ist. Pascal starb im Alter von 39 Jahren in Paris.
Erklärung des Pascalschen Prinzips
Das folgende Experiment ist recht einfach: Ein U-Rohr ist mit Wasser gefüllt und an jedem Ende sind Stopfen angebracht, die wie Kolben reibungslos und leicht gleiten können. Es wird Druck auf den linken Kolben ausgeübt, der ein wenig sinkt, und es wird beobachtet, dass der rechte Kolben ansteigt und von der Flüssigkeit gedrückt wird (Abbildung unten)..
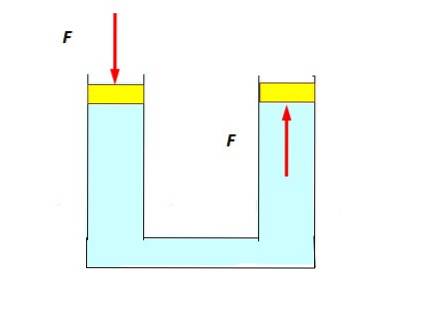
Dies geschieht, weil der Druck ohne Abnahme auf alle Punkte der Flüssigkeit übertragen wird, einschließlich derjenigen, die mit dem Kolben auf der rechten Seite in Kontakt stehen..
Flüssigkeiten wie Wasser oder Öl sind inkompressibel, gleichzeitig haben die Moleküle eine ausreichende Bewegungsfreiheit, wodurch der Druck auf den rechten Kolben verteilt werden kann..
Dank dessen erhält der rechte Kolben eine Kraft, die in Größe und Richtung genau der Kraft entspricht, die auf den linken, aber in die entgegengesetzte Richtung ausgeübt wird..
Der Druck in einer statischen Flüssigkeit ist unabhängig von der Form des Behälters. Es wird in Kürze gezeigt, dass der Druck linear mit der Tiefe variiert und das Pascalsche Prinzip eine Folge davon ist..
Eine Druckänderung an einem beliebigen Punkt bewirkt, dass sich der Druck an einem anderen Punkt um den gleichen Betrag ändert. Andernfalls würde ein zusätzlicher Druck auftreten, der die Flüssigkeit zum Fließen bringt.
Das Verhältnis zwischen Druck und Tiefe
Eine ruhende Flüssigkeit übt eine Kraft auf die Wände des Behälters, in dem sie sich befindet, und auch auf die Oberfläche eines darin eingetauchten Objekts aus. In Pascals Spritzenexperiment ist zu sehen, dass die Wasserstrahlen herauskommen senkrecht zur Kugel.
Die Flüssigkeiten verteilen die Kraft senkrecht auf die Oberfläche, auf die sie wirken. Deshalb ist es zweckmäßig, das Konzept des Durchschnittsdrucks einzuführen P.m als die senkrechte Kraft ausgeübt F.⊥ Nach Gebiet ZU, deren SI-Einheit ist der Pascal:
P.m = F.⊥ / TO
Der Druck steigt mit der Tiefe. Es kann gesehen werden, indem ein kleiner Teil der Flüssigkeit im statischen Gleichgewicht isoliert und das zweite Newtonsche Gesetz angewendet wird:
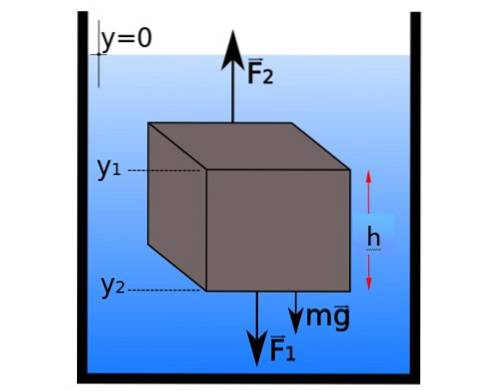
Die horizontalen Kräfte heben sich paarweise auf, aber in vertikaler Richtung sind die Kräfte wie folgt gruppiert:
∑FY. = F.zwei - F.1 - mg = 0 → F.zwei - F.1 = mg
Masse als Dichte ausdrücken ρ = Masse / Volumen:
P.zwei.A- P.1.A = ρ x Volumen x g
Das Volumen des Flüssigkeitsanteils ist das Produkt A x h:
A. (P.zwei - P.1) = ρ x A x h x g
ΔP = ρ.g.h. Grundsatz der Hydrostatik
Anwendungen

Das Pascal-Prinzip wurde verwendet, um zahlreiche Geräte zu bauen, die die Kraft vervielfachen und Aufgaben wie das Heben von Gewichten, das Stempeln auf Metall oder das Pressen von Gegenständen erleichtern. Unter ihnen sind:
-Die hydraulische Presse
-Das Auto-Bremssystem
-Mechanische Schaufeln und mechanische Arme
-Der Hydraulikzylinder
-Kräne und Aufzüge
Als nächstes wollen wir sehen, wie Pascals Prinzip kleine Kräfte in große Kräfte verwandelt, um all diese Aufgaben zu erledigen. Die hydraulische Presse ist das charakteristischste Beispiel und wird nachstehend analysiert.
Die hydraulische Presse

Um eine hydraulische Presse zu bauen, wird dieselbe Vorrichtung wie in der obigen Abbildung verwendet, dh ein U-förmiger Behälter, von dem wir bereits wissen, dass dieselbe Kraft von einem Kolben auf den anderen übertragen wird. Der Unterschied liegt in der Größe der Kolben. Dadurch funktioniert das Gerät.
Die folgende Abbildung zeigt das Prinzip von Pascal in Aktion. Der Druck ist an allen Stellen in der Flüssigkeit gleich, sowohl im kleinen als auch im großen Kolben:
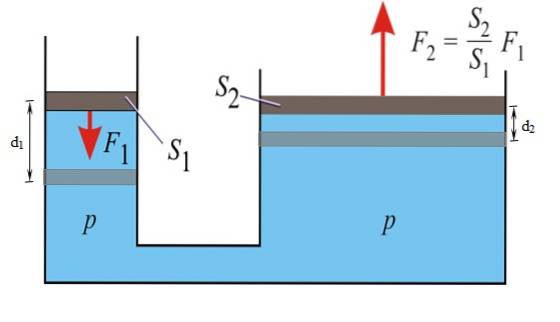
p = F.1 / S.1 = F.zwei / S.zwei
Die Größe der auf den großen Kolben übertragenen Kraft beträgt:
F.zwei = (S.zwei / S.1). F.1
Likeszwei > S.1, ergibt F.zwei > F.1, Daher wurde die Ausgangskraft mit dem Faktor multipliziert, der durch den Quotienten zwischen den Flächen gegeben ist.
Beispiele
Dieser Abschnitt enthält Anwendungsbeispiele.
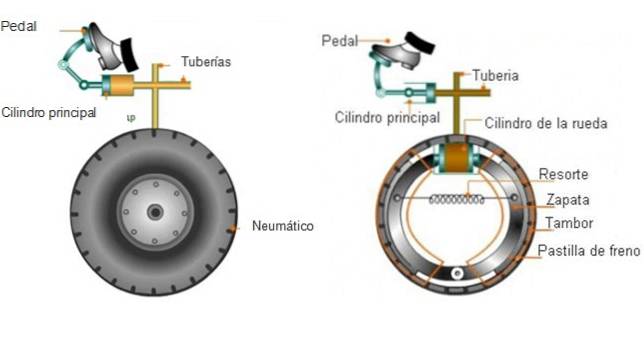
Hydraulische Bremsen
Auto-Bremsen nutzen das Pascal-Prinzip durch eine Hydraulikflüssigkeit, die die mit den Rädern verbundenen Rohre füllt. Wenn er anhalten muss, übt der Fahrer eine Kraft aus, indem er das Bremspedal betätigt und Flüssigkeitsdruck erzeugt.
Im anderen Extremfall drückt der Druck die Bremsbeläge gegen die Trommel oder die Bremsscheiben, die sich in Verbindung mit den Rädern (nicht den Reifen) drehen. Die resultierende Reibung bewirkt, dass die Scheibe stoppt und auch die Räder verlangsamt.
Mechanischer Vorteil der hydraulischen Presse
Bei der hydraulischen Presse in der folgenden Abbildung muss die Eingangsarbeit gleich der Ausgangsarbeit sein, solange die Reibung nicht berücksichtigt wird..

Eingangskraft F.1 bewirkt, dass der Kolben eine Strecke zurücklegt d1 nach unten gehen, während die Ausgangskraft F.zwei erlaubt eine Tour dzwei des ansteigenden Kolbens. Wenn die mechanische Arbeit beider Kräfte gleich ist:
F.1.d1 = F.zwei. dzwei
Der mechanische Vorteil M ist der Quotient zwischen den Größen der Eingangskraft und der Ausgangskraft:
M = F.zwei/ F.1 = d1/ dzwei
Und wie im vorherigen Abschnitt gezeigt, kann es auch als Quotient zwischen den Bereichen ausgedrückt werden:
F.zwei/ F.1 = S.zwei / S.1
Es scheint, dass die Arbeit kostenlos ausgeführt werden kann, aber in Wahrheit wird mit dieser Vorrichtung keine Energie erzeugt, da der mechanische Vorteil auf Kosten der Verschiebung des kleinen Kolbens d erzielt wird1.
Um die Leistung zu optimieren, wird dem Gerät ein Ventilsystem hinzugefügt, so dass der Auslasskolben dank kurzer Impulse auf den Einlasskolben ansteigt..
Auf diese Weise pumpt der Bediener eines hydraulischen Wagenhebers mehrmals, um ein Fahrzeug schrittweise anzuheben..
Übung gelöst
In der hydraulischen Presse von 5 sind die Kolbenflächen 0,5 Quadratzoll (kleiner Kolben) und 25 Quadratzoll (großer Kolben). Finden:
a) Der mechanische Vorteil dieser Presse.
b) Die Kraft, die erforderlich ist, um eine 1-Tonnen-Last anzuheben.
c) Der Abstand, den die Eingangskraft ausüben muss, um die Last um 1 Zoll anzuheben.
Drücken Sie alle Ergebnisse in Einheiten des britischen Systems und des SI International System aus.
Lösung
a) Der mechanische Vorteil ist:
M = F.zwei/ F.1 = S.zwei/ S.1 = 25 inzwei / 0,5 inzwei = 50
b) 1 Tonne entspricht 2000 lb-Kraft. Die erforderliche Kraft ist F.1::
F.1 = F.zwei / M = 2000 lb-Kraft / 50 = 40 lb-Kraft
Um das Ergebnis im internationalen System auszudrücken, ist der folgende Umrechnungsfaktor erforderlich:
1 lb-Kraft = 4.448 N.
Daher beträgt die Größe von F1 177,92 N..
c) M = d1/ d2 → d1 = M.d.zwei = 50 x 1 Zoll = 50 Zoll
Der erforderliche Umrechnungsfaktor beträgt: 1 Zoll = 2,54 cm
d1 = 127 cm = 1,27 m
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill. 417-450.
- Hochschulphysik. Pascal beginnt. Wiederhergestellt von: opentextbc.ca.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 4. Flüssigkeiten und Thermodynamik. Herausgegeben von Douglas Figueroa (USB). 4 - 12.
- Rex, A. 2011. Grundlagen der Physik. Pearson. 246-255.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. McGraw Hill. 301-320.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.