
Steigung einer Linienformel und Gleichungen, Darstellung, Beispiele
Das Steigung einer Linie ist die Tangente des Winkels θ, den die Linie mit der horizontalen Achse bildet, die üblicherweise gegen den Uhrzeigersinn gemessen wird. Die Steigung einer Linie ist immer konstant und deshalb eine ihrer wichtigsten Eigenschaften..
Um es zu berechnen, müssen Sie zwei Punkte auf der Linie kennen, deren Koordinaten (x) sind1,Y.1) und (xzwei,Y.zwei). Ein Segment, das zur Linie gehört, wird zwischen beiden Punkten gezeichnet, und dann werden die Segmente gezeichnet, die den Abstand zwischen x darstellen.1 und xzwei, und zwischen und1 und undzwei, wie in der Abbildung unten.
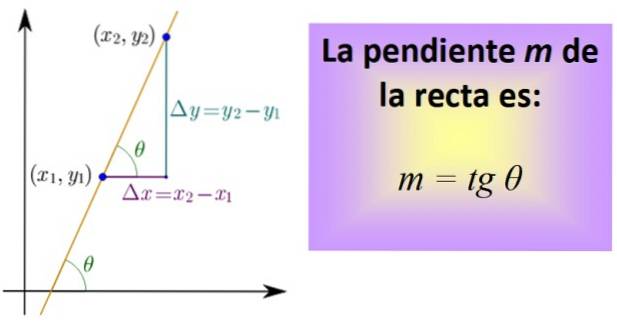
Die drei Segmente bilden ein rechtwinkliges Dreieck mit den Beinen: Δx = xzwei - x1 y Δy = yzwei - Y.1. Sie entsprechen jeweils einer horizontalen und einer vertikalen Verschiebung..
Nun definieren wir einen Quotienten, der als Tangente des Winkels θ und abgekürzt tg θ bezeichnet wird und genau die Steigung ist m der geraden:
m = tg & thgr; = & Dgr; y / & Dgr; x
Beachten Sie, dass dieser Winkel für eine Linie unabhängig von den Punkten, die zur Berechnung ihrer Tangente verwendet werden, konstant bleibt. In jedem Fall gibt dieser Wert ein Maß dafür, wie steil die Linie ist.
Durch die Koordinaten der ausgewählten Punkte lautet die Formel für die Steigung:
m = (y - y1 ) / (xzwei - x1)
Artikelverzeichnis
- 1 Grafische Darstellung
- 2 Arten von Steigungen
- 3 Wie berechnet man die Steigung einer Linie??
- 4 Gelöste Übungen
- 4.1 - Übung 1
- 4.2 - Übung 2
- 5 Beispiele
- 5.1 Beispiel 1
- 5.2 Beispiel 2
- 6 Referenzen
Grafische Darstellung
Nachfolgend haben wir einige Situationen, in denen das Konzept der Steigung relevant ist. Sein Wert kann leicht berechnet werden, indem die jeweilige vertikale und horizontale Verschiebung gemessen und dann der am Anfang angegebene Quotient erstellt wird.
Dies gibt uns eine Vorstellung von der Unebenheit oder dem Niedergang einer Struktur wie einer Rampe, eines Daches oder einer Straße:
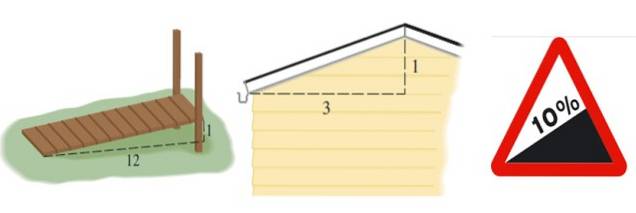
Die Neigung der in Abbildung 2 links gezeigten Rampe beträgt m = 1/12, die des Daches m = 1/3 und die der Straße als Prozentsatz. Ein Prozentsatz von 10% bedeutet, dass pro 100 Meter, die horizontal vorrücken, 10 Meter Höhe gewonnen werden:
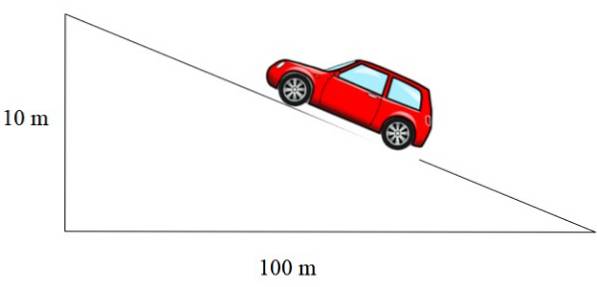
In diesem Fall beträgt die Steigung 10/100 = 0,1, was als Prozentsatz ausgedrückt 10% entspricht..
Pistenarten
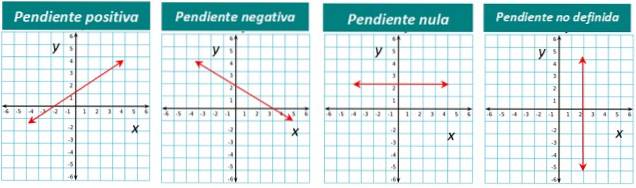
Die Steigung einer Linie kann positiv, negativ oder null sein. Beispielsweise hat die in Abbildung 1 gezeigte Linie eine positive Steigung. Wir schätzen es sofort, weil wir sehen, dass die Linie "steigt", wenn wir sie von links nach rechts sehen.
Wenn die Linie von links nach rechts abfällt, ist ihre Steigung negativ. Und wenn eine Linie horizontal ist, ist ihre Steigung Null.
Schließlich ist für vertikale Linien die Steigung nicht definiert.
Die grafische Darstellung jedes Typs ist unten:
Wie berechnet man die Steigung einer Linie??
Die Berechnung der Steigung ist sehr einfach. Sie müssen nur die vertikale und die horizontale Verschiebung ermitteln und dann den Quotienten zwischen beiden erstellen.
Wenn wir die Zeichnung der Linie in der kartesischen Ebene haben, werden diese Verschiebungen durch Auswahl von zwei beliebigen Punkten auf der Linie P gefunden1 Und Pzwei, Bestimmen der Koordinaten und Anwenden der am Anfang angegebenen Definition:
m = (y - y1 ) / (xzwei - x1 )
Da der Wert der Steigung unabhängig von der Wahl von P ist1 Und Pzwei , Wir werden einen Punkt P für eine der Koordinaten (x, y) wählen, die zur Linie gehören, deren Koordinaten nicht bekannt sind, und einen anderen Punkt P.1 deren Koordinaten sind: (x1,Y.1).
Die Steigung ist:
m = (y - y1) / (x - x1)
Wir können das klären Y.::
und und1 = m (x - x1)
Nehmen wir nun diesen Punkt P an1 ist der Schnittpunkt der Linie mit der vertikalen Achse der Koordinaten (0, b). Einsetzen in die obige Gleichung:
y - b = m (x - 0) → y = mx + b
Dieser Ausdruck ist als die Gleichung der Linie in der Form bekannt Steigung - Achsenabschnitt, da die Linie eindeutig bestimmt wird, wenn ihre Neigung und ihr Schnittpunkt mit der vertikalen Achse bekannt sind.
Nur die Steigung zu kennen, reicht nicht aus, um eine Linie in der Ebene zu charakterisieren, da unendliche Linien dieselbe Steigung haben können, was bedeutet, dass sie parallel sind, aber durch andere Punkte verlaufen.
Gelöste Übungen
- Übung 1
Finden Sie die Steigung der in der folgenden Abbildung gezeigten Linie:
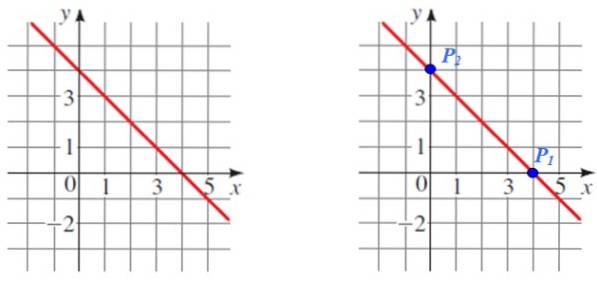
Lösung
P.1 Und Pzwei sind zwei leicht lesbare Punkte, die für die Berechnung verwendet werden. Beachten Sie auch, dass es sich um die jeweiligen Schnittpunkte mit den Koordinatenachsen handelt.
Die Koordinaten jedes Punktes sind:
P.1 (4.0) und P.zwei (0,4)
Durch Einsetzen der Steigung in die Gleichung:
m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1
Die Steigung ist negativ, was nach Betrachtung des Diagramms zu erwarten war.
- Übung 2
Finden Sie die Gleichung der Linie, die durch den Punkt (1, -6) verläuft und parallel zur Linie y = 2x - 3 verläuft.
Lösung
Die Steigung der gesuchten Linie muss dieselbe sein wie die von y = 2x - 3, da sie parallel sind. Für diese Linie ist die Steigung m = 2, daher hat die gesuchte die folgende Form:
und und1 = 2 (x - x1)
Jetzt ersetzen wir den Punkt, durch den unsere Linie verläuft: x1 = 1 und y1 = -6.
y - (-6) = 2 (x - 1)
Daher ist y = 2x - 2 - 6 → y = 2x - 8
Beispiele
Zwei Größen können so in Beziehung gesetzt werden, dass ihr Graph eine gerade Linie ist. In diesem Fall wird gesagt, dass die Größen eine lineare Abhängigkeit haben und die Steigung der Linie als die Änderungsrate von einer Variablen zur anderen interpretiert werden kann.
Beispiel 1
Angenommen, ein Pool ist an einem mit Wasser gefüllt Bewertung zeitlich konstant. Je mehr Zeit vergeht, desto mehr Wasser wird natürlich gespeichert. Nun, die Geschwindigkeit, mit der der Pool gefüllt wird, ist genau die Steigung der Linie, die das Volumen mit der Zeit in Beziehung setzt:
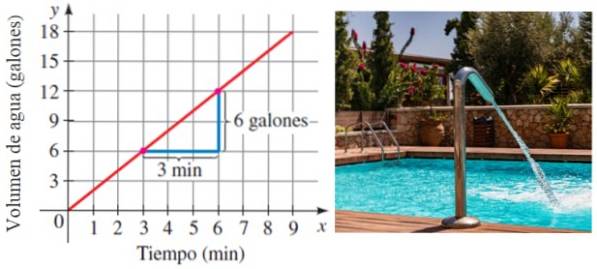
In diesem Beispiel füllt sich der Pool mit einer Geschwindigkeit von 6/3 Gallonen pro Minute oder 2 Gallonen / Minute.
Beispiel 2
Wenn sich ein Mobiltelefon in einer geraden Linie mit konstanter Geschwindigkeit bewegt, ist die Steigung des Positionsgraphen als Funktion der Zeit nichts anderes als diese Geschwindigkeit. Die Grafik zeigt ein Mobiltelefon mit positiver Geschwindigkeit, was bedeutet, dass es sich vom Ursprung wegbewegt.
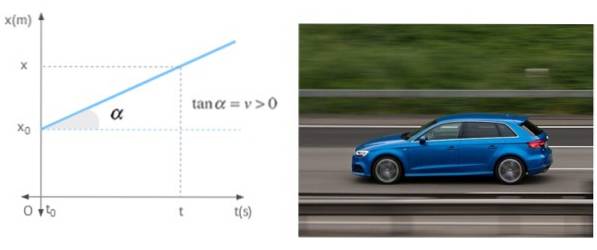
Verweise
- Alvarez, J. Der Hang einer Autobahn. Wiederhergestellt von: geogebra.es.
- Carena, M. 2019. Voruniversitäres Mathematikhandbuch. Nationale Universität des Litoral.
- Hoffman, J. Auswahl mathematischer Themen. Band 4.
- Jiménez, R. 2008. Algebra. Prentice Halle.
- Stewart, J. 2006. Precalculus: Mathematik für Calculus. 5 .. Auflage. Lernen einbinden.
- Zill, D. 1984. Algebra und Trigonometrie. Mcgraw Hügel.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.