Imaginäre Zahlen Eigenschaften, Anwendungen, Beispiele

Das imaginäre Zahlen sind diejenigen, die eine Lösung für die Gleichung geben, in der das Unbekannte im Quadrat einer negativen reellen Zahl entspricht. Die imaginäre Einheit ist i = √ (-1).

In der Gleichung: z^zwei= - a, z ist eine imaginäre Zahl, die wie folgt ausgedrückt wird:

 z = √ (-a) = i√ (a)

Sein zu eine positive reelle Zahl. Ja a = 1, dann z = i, wo ich ist die imaginäre Einheit.

Im Allgemeinen wird eine reine imaginäre Zahl z immer in folgender Form ausgedrückt: 

z = y⋅i

Wo Y. ist eine reelle Zahl e ich ist die imaginäre Einheit.

So wie reelle Zahlen in einer Linie dargestellt werden, die als bezeichnet wird echt gerade, in analoger Weise werden die imaginären Zahlen auf der dargestellt imaginäre Linie.

Das imaginäre Linie ist immer orthogonal (90º Form) zum echt gerade und die zwei Linien definieren eine kartesische Ebene, die als bezeichnet wird komplexe Ebene.

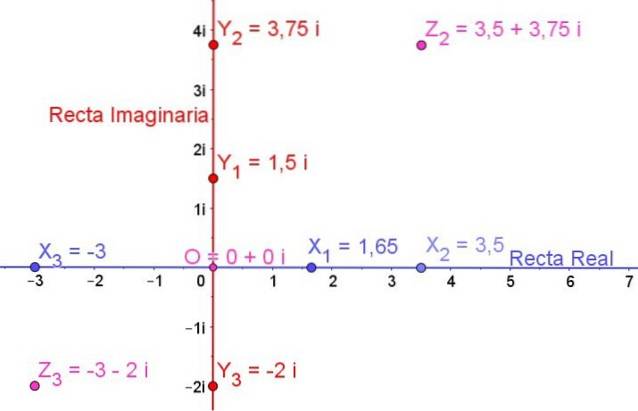
In Abbildung 1 ist die komplexe Ebene dargestellt, auf der einige reelle Zahlen, einige imaginäre Zahlen und auch einige komplexe Zahlen dargestellt sind:

X.₁, X._zwei, X.₃ Sie sind reelle Zahlen

Y.₁, Y._zwei, Y.₃ es sind imaginäre Zahlen

Z._zwei und Z.₃ Sie sind komplexe Zahlen

Die Zahl O ist die reale Null und es ist auch die imaginäre Null, so dass der Ursprung O die komplexe Null ist, ausgedrückt durch:

0 + 0i 

Artikelverzeichnis

• 1 Eigenschaften
  • 1.1 Addition und Subtraktion von Imaginärem
  • 1.2 Produkt von Imaginaries
  • 1.3 Produkt einer reellen Zahl von einem anderen Imaginären
  • 1.4 Ermächtigung eines Imaginären
  • 1.5 Summe einer reellen Zahl und einer imaginären Zahl
• 2 Anwendungen
• 3 Übungen mit imaginären Zahlen
  • 3.1 - Übung 1
  • 3.2 - Übung 2
  • 3.3 - Übung 3
  • 3.4 - Übung 4
  • 3.5 - Übung 5
  • 3.6 - Übung 6
• 4 Referenzen

Eigenschaften

Die Menge der imaginären Zahlen wird bezeichnet mit:

I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…

Und Sie können einige Operationen für diesen numerischen Satz definieren. Aus diesen Operationen wird nicht immer eine imaginäre Zahl erhalten. Schauen wir sie uns also etwas genauer an:

Addition und Subtraktion von Imaginärem

Imaginäre Zahlen können addiert und voneinander subtrahiert werden, was zu einer neuen imaginären Zahl führt. Beispielsweise:

 3i + 2i = 5i

4i - 7i = -3i

Produkt des Imaginären

Wenn das Produkt einer imaginären Zahl mit einer anderen hergestellt wird, ist das Ergebnis eine reelle Zahl. Führen Sie die folgenden Schritte aus, um dies zu überprüfen:

2i x 3i = 6 x i^zwei = 6 x (√ (-1))^zwei = 6 x (-1) = -6.

Und wie wir sehen können, ist -6 eine reelle Zahl, obwohl sie durch Multiplikation zweier reiner imaginärer Zahlen erhalten wurde.

Produkt einer reellen Zahl von einem anderen Imaginären

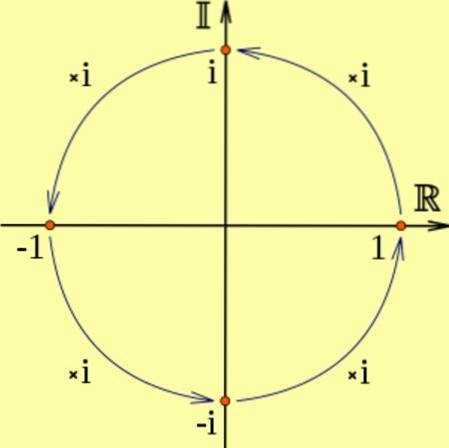
Wenn eine reelle Zahl mit i multipliziert wird, ist das Ergebnis eine imaginäre Zahl, die einer Drehung um 90 Grad gegen den Uhrzeigersinn entspricht.

Und es ist so, dass ich^zwei entspricht zwei aufeinanderfolgenden Umdrehungen von 90 Grad, was einer Multiplikation mit -1 entspricht, d. h. i^zwei = -1. Es ist in der folgenden Abbildung zu sehen:

Beispielsweise:

-3 x 5i = -15i

-3 x i = -3i.

Ermächtigung eines Imaginären

Sie können die Potenzierung einer imaginären Zahl zu einem ganzzahligen Exponenten definieren:

ich¹ = i

ich^zwei = i x i = √ (-1) x √ (-1) = -1

ich³ = i x i^zwei = -i

ich⁴ = i^zwei x i^zwei = -1 x -1 = 1

ich⁵ = i x i⁴ = i

Im Allgemeinen muss man ichⁿ = i ^ (n mod 4), wo mod ist der Rest der Teilung zwischen n Y. 4.

Eine negative ganzzahlige Potenzierung kann ebenfalls durchgeführt werden:

ich^-1 = 1 / i¹ = i / (i x i¹) = i / (i^zwei) = i / (-1) = -i

ich-^zwei = 1 / i^zwei = 1 / (-1) = -1

ich-³= 1 / i³ = 1 / (- i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Im Allgemeinen ist die auf die Potenz n erhobene imaginäre Zahl b⋅i:

(b⋅i) iⁿ = bⁿ ichⁿ = bⁿ i ^ (n mod 4)

Einige Beispiele sind die folgenden:

(5 i)¹² = 5¹² ich¹² = 5¹² ich⁰ = 5¹² x 1 = 244140625

(5 i)^elf = 5^elf ich^elf = 5^elf ich³ = 5^elf x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ ich¹⁰ = 2¹⁰ ich^zwei = 1024 x (-1) = -1024

Summe einer reellen Zahl und einer imaginären Zahl

Wenn Sie eine reelle Zahl mit einer imaginären Zahl hinzufügen, ist das Ergebnis weder reell noch imaginär. Es handelt sich um eine neue Art von Zahl, die aufgerufen wird komplexe Zahl.

Wenn beispielsweise X = 3,5 und Y = 3,75i ist, ist das Ergebnis die komplexe Zahl:

Z = X + Y = 3,5 + 3,75 i

Beachten Sie, dass in der Summe der Real- und der Imaginärteil nicht zusammen gruppiert werden können, sodass eine komplexe Zahl immer einen Realteil und einen Imaginärteil hat..

Diese Operation erweitert den Satz reeller Zahlen auf die breitesten komplexen Zahlen.

Anwendungen

Der Name der imaginären Zahlen wurde vom französischen Mathematiker René Descartes (1596-1650) als Spott oder Widerspruch zu dem Vorschlag des italienischen Mathematikers Raffaelle Bombelli aus dem Jahrhundert vorgeschlagen.

Andere große Mathematiker wie Euler und Leibniz unterstützten Descartes bei dieser Meinungsverschiedenheit und nannten imaginäre Zahlen Amphibienzahlen, das war zwischen Sein und Nichts hin und her gerissen.

Der Name der imaginären Zahlen bleibt bis heute erhalten, aber ihre Existenz und Bedeutung ist sehr real und greifbar, da sie in vielen Bereichen der Physik auf natürliche Weise vorkommen, wie zum Beispiel:

-Die Relativitätstheorie.

-Im Elektromagnetismus.

-Quantenmechanik.

Übungen mit imaginären Zahlen

- Übung 1

Finden Sie die Lösungen der folgenden Gleichung:

z^zwei + 16 = 0

Lösung

z^zwei = -16

Wir haben in beiden Mitgliedern eine Quadratwurzel:

√ (z^zwei ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Mit anderen Worten sind die Lösungen der ursprünglichen Gleichung:

z = + 4i oder z = -4i.

- Übung 2

Finden Sie das Ergebnis der Anhebung der imaginären Einheit auf die Potenz 5 abzüglich der Subtraktion der imaginären Einheit, die auf die Potenz -5 angehoben wurde.

Lösung

ich⁵ - ich-⁵ = i⁵ - 1 / i⁵ = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i

- Übung 3

Finden Sie das Ergebnis der folgenden Operation:

(3i)³ + 9i 

Lösung

3³ ich³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Übung 4

Finden Sie die Lösungen der folgenden quadratischen Gleichung:

(-2x)^zwei + 2 = 0

Lösung

Die Gleichung wird wie folgt neu angeordnet:

(-2x)^zwei = -2

Dann wird die Quadratwurzel beider Mitglieder gezogen

√ ((- 2x)^zwei) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Dann lösen wir nach x, um endlich zu erhalten:

x = ± √2 / 2 i

Das heißt, es gibt zwei mögliche Lösungen:

x = (√2 / 2) i

Oder dieses andere:

x = - (√2 / 2) i

- Übung 5

Finden Sie den Wert von Z definiert durch:

Z = √ (-9) √ (-4) + 7

Lösung

Wir wissen, dass die Quadratwurzel einer negativen reellen Zahl eine imaginäre Zahl ist, zum Beispiel ist √ (-9) gleich √ (9) x √ (-1) = 3i.

Andererseits ist √ (-4) gleich √ (4) x √ (-1) = 2i.

Die ursprüngliche Gleichung kann also ersetzt werden durch:

3i x 2i - 7 = 6 i^zwei - 7 = 6 (-1) - 7 = -6 - 7 = -13

- Übung 6

Finden Sie den Wert von Z, der sich aus der folgenden Division zweier komplexer Zahlen ergibt:

Z = (9 - i^zwei) / (3 + i)

Lösung

Der Zähler des Ausdrucks kann mit der folgenden Eigenschaft berücksichtigt werden:

Eine Differenz der Quadrate ist das Produkt aus der Summe und der Differenz der Binome ohne Quadratur.

Dann:

Z = [(3 - i) (3 + i)] / (3 + i)

Der resultierende Ausdruck wird dann vereinfacht, so dass

Z = (3 - i)

Verweise

1. Earl, R. Komplexe Zahlen. Wiederhergestellt von: maths.ox.ac.uk.
2. Figuera, J. 2000. Mathematik 1 .. Diversifiziert. CO-BO-Ausgaben.
3. Hoffmann, J. 2005. Auswahl mathematischer Themen. Monfort Veröffentlichungen.
4. Jiménez, R. 2008. Algebra. Prentice Halle.
5. Wikipedia. Imaginäre Zahl. Wiederhergestellt von: en.wikipedia.org