
Winkel gegenüber dem Scheitelpunkt (mit gelöster Übung)
Das Gegenüberliegende Winkel durch den Scheitelpunkt sind diejenigen, die Folgendes erfüllen: Die Seiten eines von ihnen sind die Verlängerungen der Seiten des anderen Winkels. Das Grundsatz Von den Winkeln, denen der Scheitelpunkt gegenübersteht, heißt es: Zwei Winkel, denen der Scheitelpunkt gegenüberliegt, haben das gleiche Maß.
Die Sprache wird oft missbraucht, indem gesagt wird, dass die Winkel gegenüber dem Scheitelpunkt gleich sind, was nicht korrekt ist. Nur weil zwei Winkel das gleiche Maß haben, heißt das nicht, dass sie gleich sind. Es ist, als würde man sagen, dass zwei gleich große Kinder gleich sind.
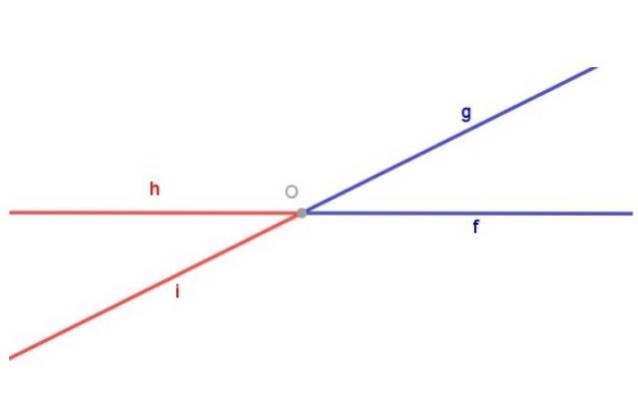
Denken Sie daran, dass ein Winkel als die geometrische Figur definiert ist, die aus zwei Strahlen mit demselben Ursprung besteht.
Abbildung 1 zeigt den Winkel Nebel (blau) zusammengesetzt aus dem Strahl [Von) und der Strahl [Og] gemeinsamen Ursprungs ODER. Abbildung 1 zeigt auch den Winkel hOi (rot) zusammengesetzt aus dem Strahl [Ich hörte) und der Strahl [Oh) beide mit Herkunft ODER.
Zwei Winkel, denen der Scheitelpunkt gegenübersteht, sind zwei verschiedene geometrische Figuren. Um dies hervorzuheben, wurde in Abbildung 1 der Winkel eingefärbt Nebel blau, während der Winkel hOi wurde rot gefärbt.
Die blauen und roten Winkel in Abbildung 1 sind am Scheitelpunkt entgegengesetzt, weil: der Strahl [Von) des blauen Winkels ist die Verlängerung des Strahls [Oh) des roten Winkels und des Strahls [Og] des blauen Winkels ist die Verlängerung des Strahls [Ich hörte) des roten Winkels.
Artikelverzeichnis
- 1 Wichtige Konzepte zu Winkeln
- 1.1 Seiten und Eckpunkte eines Winkels
- 1.2 Winkel, die durch zwei sich schneidende Linien gebildet werden
- 2 Senkrechte Linien und rechter Winkel
- 2.1 Strahlen auf derselben Linie und demselben Ebenenwinkel
- 2.2 Nullwinkel und Vollwinkel
- 3 Winkelmessung
- 3.1 Sexagesimalsystem
- 4 Satz der Scheitelwinkel
- 4.1 Demo
- 5 Übung gelöst
- 5.1 Lösung
- 6 Referenzen
Wichtige Konzepte zu Winkeln
Seiten und Eckpunkte eines Winkels
Die geometrische Figur, die aus zwei Strahlen mit gemeinsamem Ursprung besteht, ist ein Winkel. Das folgende Bild zeigt den Winkel POQ gebildet durch die zwei Strahlen [OP] Y. [OQ] gemeinsamen Ursprungs ODER:
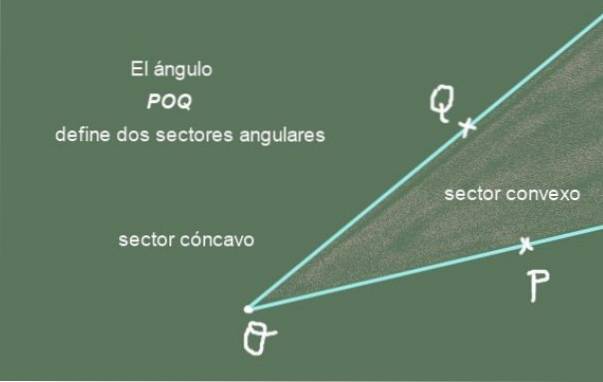
Die Strahlen [OP] Y. [OQ] sind die Winkelseiten POQ, während der gemeinsame Punkt O genannt wird Winkelscheitelpunkt.
Winkelsektor: Ein Winkel teilt die Ebene, die ihn enthält, in zwei Winkelsektoren. Einer von ihnen ist der konvexe Winkelsektor und der andere ist der konkave Winkelsektor. Die Vereinigung der beiden Sektoren ergibt die vollständige Ebene.
Abbildung 2 zeigt den Winkel POQ und seine zwei Winkelsektoren. Der konvexe Winkelsektor ist derjenige mit einer spitzen Form, während der konkave Winkelsektor der Ebene ist, der der konvexe Sektor fehlt.
Winkel, die durch zwei sich kreuzende Linien gebildet werden
Zwei sich schneidende Linien einer Ebene bilden vier Winkel und teilen die Ebene in vier Winkelsektoren.
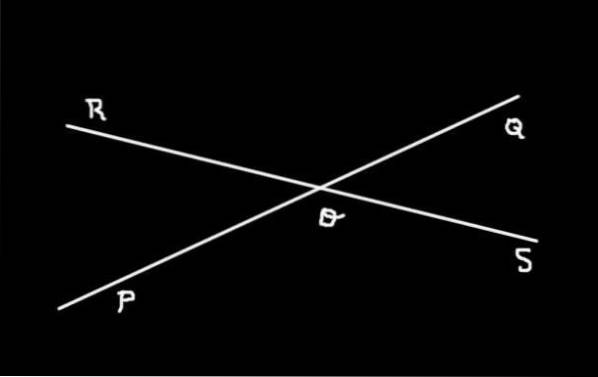
Abbildung 3 zeigt die beiden Linien (PQ) Y. (RS) die in abgefangen werden ODER. Dort ist zu sehen, dass vier Winkel bestimmt werden:
-SOQ, QOR, ROP Y. POS
Die Engel SOQ Y. QOR, QOR Y. ROP, ROP Y. POS, POS Y. SOQ Sie sind angrenzende Winkel einander während SOQ Y. ROP Sie sind am Scheitelpunkt gegenüberliegend. Sie sind auch Gegenüberliegende Winkel durch den Scheitelpunkt Die Engel QOR Y. POS.
Senkrechte Linien und rechte Winkel
Zwei Sekantenlinien (Schnittlinien) sind Senkrechte gerade Linien wenn sie vier gleich große Winkelsektoren bestimmen. Wenn jeder der vier Sektoren symmetrisch zum benachbarten Winkelsektor ist, haben sie das gleiche Maß.
Jeder der Winkel, die die beiden senkrechten Linien bestimmen, wird aufgerufen rechter Winkel. Alle rechten Winkel haben das gleiche Maß.
Strahlen auf der gleichen Linie und im gleichen Ebenenwinkel
Mit einer Linie und einem Punkt darauf werden zwei Strahlen definiert. Diese beiden Strahlen definieren zwei ebene Winkel.
In Abbildung 3 sehen Sie die Linie (RS) und der Punkt ODER welches gehört zu (RS). Der Winkel SOR ist ein ebener Winkel. Es kann auch angegeben werden, dass der Winkel ROS ist ein ebener Winkel. Alle ebenen Winkel haben das gleiche Maß.
Nullwinkel und Vollwinkel
Ein einzelner Strahl definiert zwei Winkel: Einer davon ist der des konvexen Winkelsektors Nullwinkel und das andere, das des konkaven Winkelsektors ist das voller Winkel. In Abbildung 3 sehen Sie die Nullwinkel SOS und der voller Winkel SOS.
Winkelmessung
Es gibt zwei Zahlensysteme, die häufig verwendet werden, um das Maß eines Winkels anzugeben.
Eines davon ist das Sexagesimalsystem, das auf der Zahl 60 basiert. Es ist ein Erbe der alten mesopotamischen Kulturen. Das andere System der Winkelmessung ist das Radian-System, das auf der Zahl π (pi) basiert und ein Erbe der antiken griechischen Weisen ist, die die Geometrie entwickelt haben.
Sexagesimalsystem
Nullwinkel: im sexagesimalen System misst der Nullwinkel 0º (Null Grad).
Vollwinkel: ihm wird das Maß 360º (dreihundertsechzig Grad) zugewiesen.
Ebenenwinkel: im sexagesimalen System misst der ebene Winkel 180º (einhundertachtzig Grad).
Rechter Winkel: Zwei senkrechte Linien teilen die Ebene in vier gleich große Winkel, die als rechte Winkel bezeichnet werden. Das Maß für einen rechten Winkel ist der vierte Teil des gesamten Winkels, dh 90º (neunzig Grad)..
Winkelmesser oder Goniometer
Der Winkelmesser ist das Instrument zur Winkelmessung. Es besteht aus einem Halbkreis (normalerweise durchsichtiger Kunststoff), der in 180 Winkelabschnitte unterteilt ist. Da ein Halbkreis einen ebenen Winkel bildet, beträgt das Maß zwischen zwei aufeinanderfolgenden Abschnitten 1º.
Das Goniometer ähnelt dem Winkelmesser und besteht aus einem Kreis, der in 360 Winkelabschnitte unterteilt ist.
Ein Winkel, dessen Seiten von der Mitte des Goniometers beginnen, schneidet zwei Sektoren, und das Maß dieses Winkels in Grad entspricht der Anzahl n von Abschnitten zwischen den beiden unterbrochenen Sektoren. In diesem Fall beträgt das Maß nº (es lautet „Jan Abschlüsse”).
Scheitelpunktwinkel-Theorem
Formal wird der Satz folgendermaßen ausgedrückt:
Wenn zwei Winkel vertikal entgegengesetzt sind, haben sie das gleiche Maß.
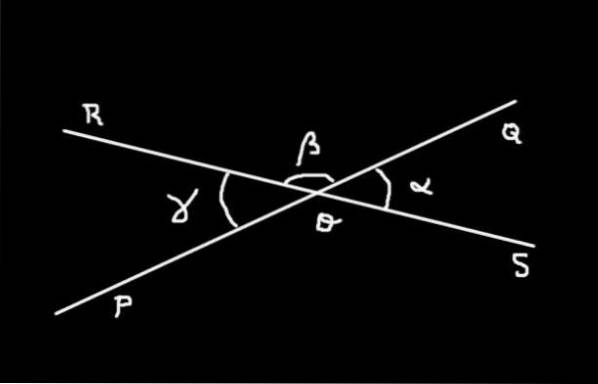
Demonstration
Der Winkel SOQ hat Maß α; der Winkel QOR hat Maß β und Winkel ROP hat Maß γ. Die Summe des Winkels SOQ mehr ihn QOR bilden den ebenen Winkel SOR 180º messen.
Das ist:
α + β = 180º
Auf der anderen Seite und unter Verwendung der gleichen Argumentation mit den Winkeln QOR Y. ROP du hast:
β + γ = 180º
Wenn wir die beiden vorhergehenden Gleichungen beobachten, ist die einzige Möglichkeit, beide zu erfüllen, dass α gleich γ ist.
Was SOQ hat das Maß α und ist dem Scheitelpunkt gegenüber entgegengesetzt ROP des Maßes γ, und da α = γ ist, wird geschlossen, dass die Winkel gegenüber dem Scheitelpunkt das gleiche Maß haben.
Übung gelöst
Bezugnehmend auf 4: Angenommen, β = 2 α. Finden Sie das Maß der Winkel SOQ, QOR Y. ROP in sexagesimalen Graden.
Lösung
Als Summe des Winkels SOQ mehr ihn QOR bilden den ebenen Winkel SOR du hast:
α + β = 180º
Aber sie sagen uns, dass β = 2 α ist. Wenn wir diesen Wert von β einsetzen, haben wir:
α + 2 α = 180º
Nämlich:
3 α = 180º
Was bedeutet, dass α der dritte Teil von 180º ist:
α = (180º / 3) = 60º
Dann das Maß von SOQ ist α = 60º. Das Maß von QOR ist β = 2 α = 2 * 60º = 120º. Endlich gerne ROP ist durch Scheitelpunkt gegenüber entgegengesetzt SOQ dann haben sie nach dem bereits bewiesenen Theorem das gleiche Maß. Das heißt, das Maß von ROP ist γ = α = 60º.
Verweise
- Baldor, J. A. 1973. Flugzeug- und Raumgeometrie. Zentralamerikanisches Kultur.
- Mathematische Gesetze und Formeln. Winkelmesssysteme. Wiederhergestellt von: ingemecanica.com.
- Wikipedia. Gegenüberliegende Winkel durch den Scheitelpunkt. Wiederhergestellt von: es.wikipedia.com
- Wikipedia. Förderer. Wiederhergestellt von: es.wikipedia.com
- Zapata F. Goniómetro: Geschichte, Teile, Betrieb. Wiederhergestellt von: lifeder.com


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.