
Beschrifteter Winkel einer Kreisdefinition, Theoreme, Beispiele
Das Beschriftungswinkel eines Kreises Es ist eines, dessen Scheitelpunkt am Umfang liegt und dessen Strahlen sekant oder tangential zu ihm sind. Infolgedessen ist der Beschriftungswinkel immer konvex oder flach..
In Abbildung 1 sind mehrere Winkel dargestellt, die in ihren jeweiligen Umfängen eingeschrieben sind. Der Winkel ∠EDF wird dadurch beschriftet, dass sein Scheitelpunkt D am Umfang liegt und seine beiden Strahlen [DE] und [DF] den Umfang schneiden.
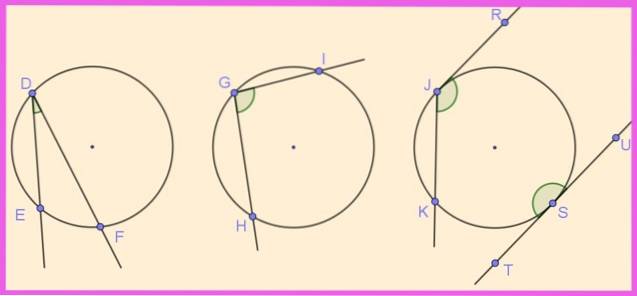
In ähnlicher Weise ist der Winkel ∠HGI eingeschrieben, da sein Scheitelpunkt am Umfang und seine Seiten an ihm anliegen.
Die Winkel ∠KJR und ∠UST sind ebenfalls am Umfang eingeschrieben. Die erste hat eine Sekantenseite und die andere Tangente, während die zweite Seite ihre beiden Seiten tangential zum Umfang hat und einen ebenen Beschriftungswinkel (180º) bildet..
Einige Autoren nennen den halb eingeschriebenen Winkel, dass eine seiner Seiten den Umfang tangiert, aber in diesem Artikel wird er als beschriftet betrachtet..
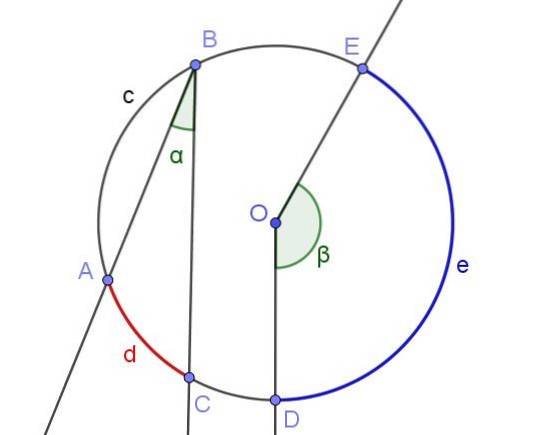
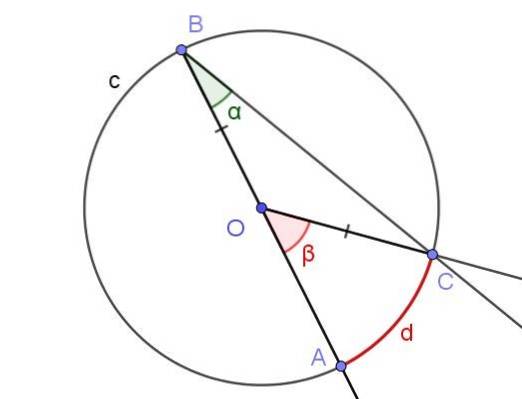
Jeder eingeschriebene Winkel definiert oder begrenzt einen damit verbundenen Bogen. Zum Beispiel begrenzt in Abbildung 2 der Beschriftungswinkel ∠ABC den Bogen A⌒C der Länge d.
Die gleiche Abbildung zeigt den Winkel ∠DOE, der nicht in den Umfang eingeschrieben ist, weil sein Scheitelpunkt nicht seinen Umfang hat, sondern in der Mitte O..
Artikelverzeichnis
- 1 Zentralwinkel
- 2 Sätze
- 2.1 - Satz 1 (Beschriftungswinkel und Mittelwinkel)
- 2.2 - Satz 2
- 2.3 - Satz 3
- 3 Beispiele
- 3.1 - Beispiel 1
- 3.2 - Beispiel 2
- 4 Referenzen
Zentralwinkel
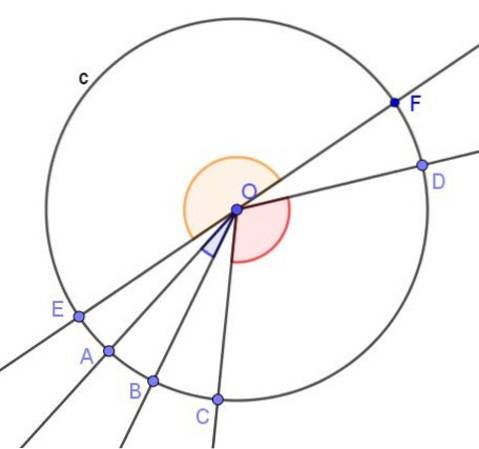
Neben dem Beschriftungswinkel wird in einem Umfang die zentraler Winkel, Dies ist derjenige, dessen Scheitelpunkt in der Mitte des Umfangs liegt und dessen Seiten den Umfang schneiden.
Das Maß im Bogenmaß eines zentralen Winkels ist der Quotient zwischen dem Teilbogen, dh dem Umfangsbogen zwischen den Seiten des Winkels, und dem Radius des Umfangs.
Wenn der Umfang einheitlich ist (mit Radius 1), ist die Länge des Bogens in denselben Radiuseinheiten das Maß für den Winkel im Bogenmaß.
Und wenn das Winkelmaß in Grad erforderlich ist, wird das Maß im Bogenmaß mit dem Faktor 180º / π multipliziert.
Winkelmessgeräte verwenden immer einen zentralen Winkel und die Länge des von ihm eingeschlossenen Bogens wird direkt in Grad kalibriert. Dies bedeutet, dass bei jeder Messung eines Winkels im Hintergrund die Länge des Bogens gemessen wird, der vom zentralen Winkel begrenzt wird.
Theoreme
- Satz 1 (Beschrifteter Winkel und Mittelwinkel)
Das Maß eines Beschriftungswinkels ist das halbe Maß des Mittelwinkels, wenn beide Winkel den gleichen Bogen bilden.
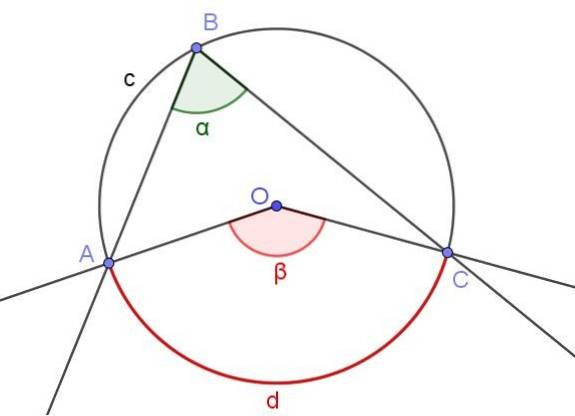
In Abbildung 4 sind zwei Winkel ∠ABC und ∠AOC dargestellt, die denselben Umfangsbogen A⌒C schneiden.
Wenn das Maß des Beschriftungswinkels α ist, ist das Maß β des Zentralwinkels doppelt so groß wie das Maß des Beschriftungswinkels (β = 2 α), da beide den gleichen Maßbogen d bilden.
Demonstration 1a
Um Satz 1 zu beweisen, werden wir zunächst einige Sonderfälle zeigen, bis wir den allgemeinen Fall erreichen.
Angenommen, ein beschrifteter Winkel, in dem eine seiner Seiten durch die Mitte des Umfangs verläuft, wie in Abbildung 5 dargestellt.
In diesem Fall wird das gleichschenklige Dreieck COB gebildet, da [OC] = [OB].
In einem gleichschenkligen Dreieck sind die Winkel neben der Basis gleich, daher ist ∠BCO = ∠ABC = α. Andererseits ist ∠COB = 180º - β.
Betrachtet man die Summe der Innenwinkel des Dreiecks COB, so ergibt sich:
α + α + (180º - β) = 180º
Daraus folgt, dass 2 α = β ist oder was äquivalent ist: α = β / 2. Dies stimmt mit dem überein, was Satz 1 besagt: Das Maß des Beschriftungswinkels ist die Hälfte des Mittelwinkels, wenn beide Winkel den gleichen Akkord bilden [AC].
Demonstration 1b
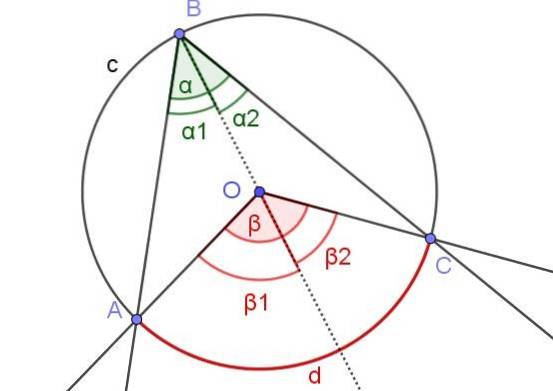
In diesem Fall haben wir einen eingeschriebenen Winkel ∠ABC, bei dem der Mittelpunkt O des Umfangs innerhalb des Winkels liegt.
Um Satz 1 in diesem Fall zu beweisen, wird der Hilfsstrahl [BO] gezeichnet, so dass wir zwei eingeschriebene Winkel ∠ABO und ∠OBC neben dem Strahl haben.
Ebenso haben wir die Mittelwinkel β1 und βzwei neben dem Strahl. Auf diese Weise haben wir die gleiche Situation wie in Beweis 1a, so dass festgestellt werden kann, dass αzwei = βzwei / 2 und α1 = β1 /zwei. Da α = α1 + αzwei und β = β1 + βzwei daher folgt, dass α = α ist1 + αzwei = β1 / 2 + βzwei / 2 = (β1 + βzwei) / 2 = β / 2.
Zusammenfassend ist α = β / 2, was Satz 1 erfüllt.
- Satz 2
Wenn zwei oder mehr eingeschriebene Winkel denselben Bogen bilden, haben sie dasselbe Maß.
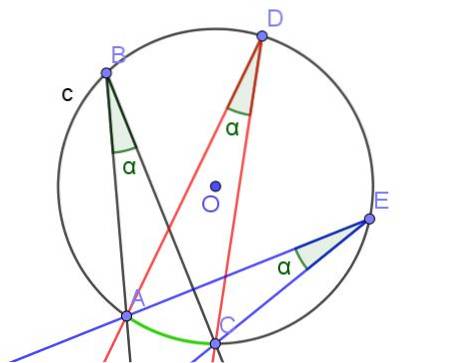
- Satz 3
Die Beschriftungswinkel, die Akkorde desselben Taktes einschließen, sind gleich.
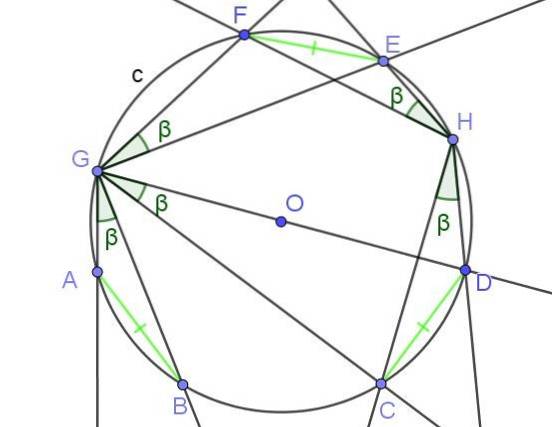
Beispiele
- Beispiel 1
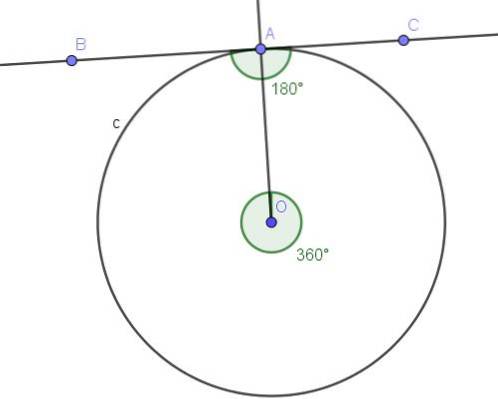
Zeigen Sie, dass der Beschriftungswinkel, der den Durchmesser begrenzt, ein rechter Winkel ist.
Lösung
Der mit dem Durchmesser verbundene zentrale Winkel ∠AOB ist ein ebener Winkel, dessen Maß 180º beträgt.
Gemäß Satz 1 hat jeder Winkel, der in den Umfang eingeschrieben ist, der denselben Akkord (in diesem Fall den Durchmesser) begrenzt, als Maß die Hälfte des zentralen Winkels, der denselben Akkord begrenzt, der in unserem Beispiel 180º / 2 = 90º beträgt.
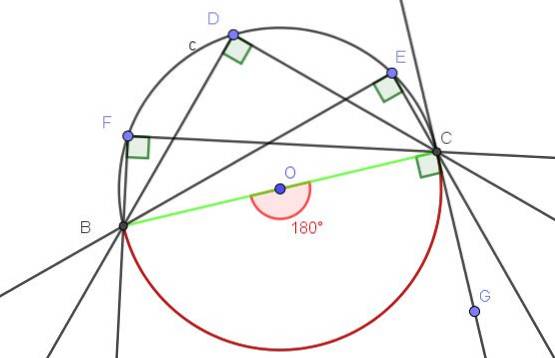
- Beispiel 2
Die Tangente der Linie (BC) an A zum Umfang C bestimmt den Beschriftungswinkel ∠BAC (siehe Abbildung 10)..
Stellen Sie sicher, dass der Satz 1 der Beschriftungswinkel erfüllt ist.
Lösung
Der Winkel ∠BAC ist eingeschrieben, weil sein Scheitelpunkt am Umfang liegt und seine Seiten [AB] und [AC) den Umfang tangieren, sodass die Definition des eingeschriebenen Winkels erfüllt ist.
Andererseits begrenzt der Beschriftungswinkel ∠BAC den Bogen A, A, der den gesamten Umfang darstellt. Der zentrale Winkel, der den Bogen A⌒A begrenzt, ist ein konvexer Winkel, dessen Maß der volle Winkel (360º) ist..
Der Beschriftungswinkel, der den gesamten Bogen begrenzt, misst die Hälfte des zugehörigen Mittelwinkels, dh ∠BAC = 360º / 2 = 180º.
Mit all dem oben Gesagten wird verifiziert, dass dieser spezielle Fall Satz 1 erfüllt.
Verweise
- Baldor. (1973). Geometrie und Trigonometrie. Zentralamerikanisches Kultur-Editorial.
- E. A. (2003). Elemente der Geometrie: mit Übungen und Geometrie des Kompasses. Universität von Medellin.
- Geometrie 1. ESO. Winkel am Umfang. Wiederhergestellt von: edu.xunta.es/
- Alle Wissenschaft. Vorgeschlagene Winkelübungen im Umfang. Wiederhergestellt von: francesphysics.blogspot.com
- Wikipedia. Beschrifteter Winkel. Wiederhergestellt von: es.wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.