
Gleichmäßig beschleunigte geradlinige Bewegungseigenschaften, Formeln
Das gleichmäßig beschleunigte geradlinige Bewegung Es ist eines, das entlang einer geraden Linie verläuft und bei dem das Mobiltelefon seine Geschwindigkeit mit einer konstanten Geschwindigkeit erhöht oder verringert. Diese Rate ist die Größe, die die Rate beschreibt, mit der sich die Geschwindigkeit ändert und aufgerufen wird Beschleunigung.
Bei gleichmäßig beschleunigten oder variierten geradlinigen Bewegungen (MRUV) ist eine konstante Beschleunigung für die Änderung der Geschwindigkeit verantwortlich. Bei anderen Bewegungsarten kann die Beschleunigung auch die Richtung und den Geschwindigkeitssinn ändern oder sogar nur die Richtung ändern, wie bei einer gleichmäßigen Kreisbewegung..

Da die Beschleunigung die Änderung der Geschwindigkeit über die Zeit darstellt, sind ihre Einheiten im internationalen System m / szwei (Meter über Sekunden im Quadrat). Wie bei der Geschwindigkeit kann der Beschleunigung ein positives oder negatives Vorzeichen zugewiesen werden, je nachdem, ob die Geschwindigkeit zunimmt oder abnimmt..
Eine Beschleunigung von etwa +3 m / szwei bedeutet, dass sich die Geschwindigkeit des Mobiltelefons mit jeder Sekunde, die vergeht, um 3 m / s erhöht. Wenn zu Beginn der Bewegung (bei t = 0) die Geschwindigkeit des Mobiltelefons +1 m / s betrug, beträgt sie nach einer Sekunde 4 m / s und nach 2 Sekunden 7 m / s.
Bei einer gleichmäßig variierten geradlinigen Bewegung werden die Geschwindigkeitsschwankungen berücksichtigt, die sich bewegende Objekte täglich erfahren. Dies ist ein realistischeres Modell als die gleichmäßige geradlinige Bewegung. Trotzdem ist es immer noch recht begrenzt, da es das Mobiltelefon einschränkt, nur auf einer geraden Linie zu fahren.
Artikelverzeichnis
- 1 Funktionen
- 1.1 Zurückgelegte Entfernung vom v vs. -Diagramm t
- 2 Formeln und Gleichungen
- 3 Gelöste Übungen
- 3.1 -Übung gelöst 1
- 3.2 - Gelöste Übung 2
- 4 Anwendungen
- 5 Referenzen
Eigenschaften
Dies sind die Hauptmerkmale einer gleichmäßig beschleunigten geradlinigen Bewegung:
-Die Bewegung verläuft immer entlang einer geraden Linie.
-Die Beschleunigung des Mobiltelefons ist sowohl in der Größe als auch in Richtung und Sinn konstant.
-Die mobile Geschwindigkeit nimmt linear zu (oder ab).
-Seit der Beschleunigung zu bleibt über die Zeit konstant t, Der Graph seiner Größe als Funktion der Zeit ist eine gerade Linie. In dem in Abbildung 2 gezeigten Beispiel ist die Linie blau gefärbt und der Beschleunigungswert wird auf der vertikalen Achse abgelesen, ungefähr +0,68 m / szwei.
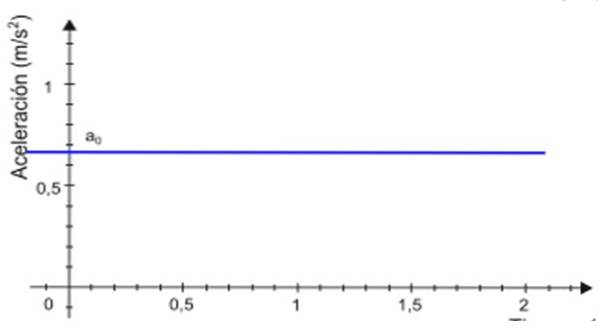
-Der Geschwindigkeitsgraph v Über t Es ist eine gerade Linie (in Abbildung 3 grün), deren Steigung der Beschleunigung des Mobiltelefons entspricht. Im Beispiel ist die Steigung positiv.

-Der Schnitt mit der vertikalen Achse gibt die Anfangsgeschwindigkeit an, in diesem Fall 0,4 m / s.
-Schließlich ist der Graph der Position x gegen die Zeit die in Abbildung 4 rot dargestellte Kurve, die immer eine Parabel ist.
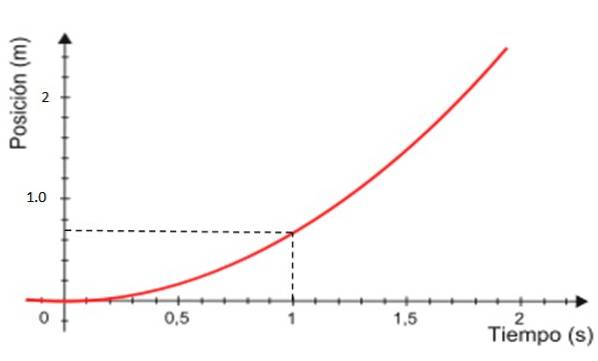
Zurückgelegte Entfernung vom v vs. Diagramm. t
Indem der Graph v vs. t Die Berechnung der vom Mobiltelefon zurückgelegten Entfernung ist sehr einfach. Die zurückgelegte Strecke entspricht der Fläche unter der Linie, die innerhalb des gewünschten Zeitintervalls liegt.
Angenommen, Sie möchten im gezeigten Beispiel die vom Mobiltelefon zurückgelegte Entfernung zwischen 0 und 1 Sekunde wissen. Verwenden Sie dieses Diagramm, siehe Abbildung 5.
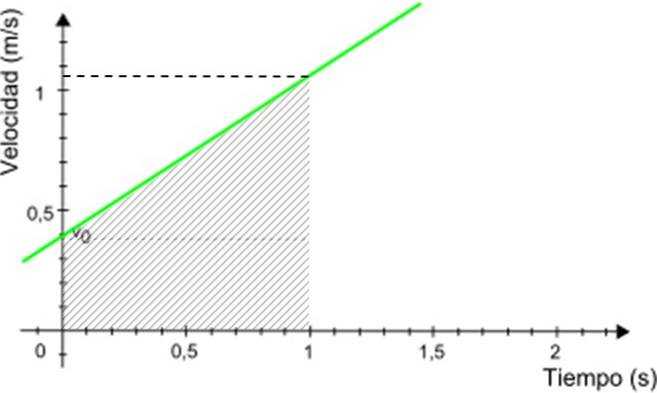
Der gesuchte Abstand entspricht numerisch der in Abbildung 3 schattierten Fläche des Trapezes. Die Fläche des Trapezes ist gegeben durch: (Hauptbasis + Nebenbasis) x Höhe / 2
Zurückgelegte Strecke = (0,4 + 1,05) x 1/2 m = 0,725 m
Es ist auch möglich, den schattierten Bereich in ein Dreieck und ein Rechteck zu unterteilen, die entsprechenden Bereiche zu berechnen und diese zu addieren. Die zurückgelegte Strecke ist positiv, auch wenn das Teilchen nach rechts oder links geht.
Formeln und Gleichungen
Sowohl die durchschnittliche Beschleunigung als auch die momentane Beschleunigung haben im MRUV den gleichen Wert, daher:
-Beschleunigung: zu = konstant
Wenn die Beschleunigung gleich 0 ist, ist die Bewegung geradlinig, da die Geschwindigkeit in diesem Fall konstant wäre. Das Zeichen von zu Es kann positiv oder negativ sein.
Da die Beschleunigung die Steigung der Linie v gegenüber t ist, lautet die Gleichung v (t):
-Geschwindigkeit als Funktion der Zeit: v (t) = voder + beim
Wo voder ist der Wert der Anfangsgeschwindigkeit des Mobiltelefons
-Position als Funktion der Zeit: x (t) = xoder + voder t + ½atzwei
Wenn Sie keine Zeit haben, sondern Geschwindigkeiten und Verschiebungen, gibt es eine sehr nützliche Gleichung, die durch Lösen der Zeit von erhalten wird v (t) = voder + beim und Ersetzen in der letzten Gleichung. Handelt von:
-Gleichung, die keine Zeit enthält: vzwei = voderzwei +2.a.Δx
Gelöste Übungen
Bei der Lösung einer Kinematikübung ist es wichtig sicherzustellen, dass die Situation an das zu verwendende Modell angepasst ist. Zum Beispiel gelten die Gleichungen der gleichmäßigen geradlinigen Bewegung nicht für die beschleunigte Bewegung.
Und diejenigen der beschleunigten Bewegung gelten beispielsweise nicht für eine kreisförmige oder krummlinige Bewegung. Die erste dieser unten gelösten Übungen kombiniert zwei Handys mit unterschiedlichen Bewegungen. Um es richtig zu lösen, ist es notwendig, zum entsprechenden Bewegungsmodell zu gehen.
-Gelöste Übung 1
Um die Tiefe eines Brunnens herauszufinden, lässt ein Kind eine Münze fallen und aktiviert gleichzeitig seinen Timer, der unmittelbar nach dem Auftreffen der Münze auf dem Wasser stoppt. Der Messwert betrug 2,5 Sekunden. Wenn Sie wissen, dass die Schallgeschwindigkeit in Luft 340 m / s beträgt, berechnen Sie die Tiefe des Bohrlochs.
Lösung
Sein h die Tiefe des Brunnens. Die Münze legt diese Strecke im freien Fall zurück, eine gleichmäßig variierte vertikale Bewegung mit einer Anfangsgeschwindigkeit von 0 beim Fallenlassen der Münze und einer konstanten Abwärtsbeschleunigung von 9,8 m / szwei. Zeit nehmen tm dabei.
Sobald die Münze auf dem Wasser aufschlägt, wandert das durch das Klicken verursachte Geräusch nach oben zum Ohr des Kindes, das die Stoppuhr stoppt, wenn es sie hört. Es gibt keinen Grund zu der Annahme, dass sich die Schallgeschwindigkeit ändert, wenn sie in den Brunnen steigt, sodass die Schallbewegung gleichmäßig geradlinig ist. Der Ton dauert eine Weile ts zum Kind kommen.
Bewegungsgleichung für die Münze:
h = ½ g.t.m zwei = 4,9 tm zwei
Wo sie ersetzt wurden x Y. zu der Gleichung für die im vorherigen Abschnitt angegebene Position durch h Y. G.
Bewegungsgleichung für Schall:
h = vs . ts = 340 ts
Es geht um die bekannte Gleichung Entfernung = Geschwindigkeit x Zeit. Mit diesen beiden Gleichungen haben wir drei Unbekannte: h, tm und ts. Für die Zeiten, in denen eine Beziehung besteht, ist bekannt, dass alles 2,5 Sekunden dauert, daher:
tm + ts = 2,5 s
Gleichstellung beider Gleichungen:
4,9 tm zwei = 340 ts
Eine der Zeiten löschen und ersetzen:
4,9 tm zwei= 340. (2,5 - tm)
Indem wir den Begriff rechts entwickeln und Begriffe umsetzen, erhalten wir:
4,9 tm zwei+340 tm - 850 = 0
Dies ist eine quadratische Gleichung mit zwei Lösungen: 2.416 und -71.8. Es wird die positive Lösung gewählt, die sinnvoll ist, da die Zeit nicht negativ sein kann und auf jeden Fall weniger als 2,5 Sekunden betragen muss. Für diese Zeit wird es durch Ersetzen der Tiefe des Brunnens erhalten:
4,9 tm zwei= 4,9 x 2,416zwei m = 28,6 m
-Übung gelöst 2
Ein mit 90 km / h fahrendes Auto nähert sich einer Kreuzung mit einer Ampel. Wenn es 70 m von dort entfernt ist, leuchtet das gelbe Licht auf, das 4 Sekunden lang anhält. Der Abstand zwischen der Ampel und der nächsten Ecke beträgt 50 m.
Der Fahrer hat zwei Möglichkeiten: a) Bremse mit - 4 m / szwei oder b) auf + 2 m / s beschleunigenzwei. Mit welcher der beiden Optionen kann der Fahrer die gesamte Allee anhalten oder überqueren, bevor die Ampel rot wird?
Lösung
Die Startposition des Fahrers ist x = 0, sobald er das gelbe Licht aufleuchten sieht. Es ist wichtig, die Einheiten richtig umzurüsten: 90 km / h entsprechen 25 m / s.
Gemäß Option a) fährt der Fahrer in den 4 Sekunden, in denen das gelbe Licht anhält, Folgendes:
x (t) = voder t + ½atzwei= 25,4 -½. (- 4) .4zweim = 68 m (Es hält 2 Meter vor der Ampel)
Analyseoption b) Wir haben:
x (t) = voder t + ½atzwei= 25.t + ½.2.t.zwei
Solange das gelbe Licht anhält, fährt der Fahrer folgendermaßen:
x = 25,4 + ½, 2,4zweim = 116 m
116 m sind jedoch weniger als die verfügbare Entfernung, um zur nächsten Ecke zu gelangen, die 70 + 50 m = 120 m beträgt. Daher kann er nicht die gesamte Straße überqueren, bevor das rote Licht aufleuchtet. Die empfohlene Maßnahme besteht darin, zu bremsen und 2 Meter von der Ampel entfernt zu bleiben.
Anwendungen
Menschen erleben die Auswirkungen der Beschleunigung täglich: beim Reisen mit dem Auto oder Bus, da diese ständig bremsen und beschleunigen müssen, um die Geschwindigkeit an die Hindernisse auf der Straße anzupassen. Beschleunigung tritt auch beim Auf- und Absteigen in einem Aufzug auf.
Vergnügungsparks sind Orte, an denen Menschen bezahlen, um die Auswirkungen der Beschleunigung zu erleben und Spaß zu haben.
In der Natur wird eine gleichmäßig variierte geradlinige Bewegung beobachtet, wenn ein Objekt frei fallen gelassen wird oder wenn es vertikal nach oben geworfen wird und darauf wartet, dass es auf den Boden zurückkehrt. Wird der Luftwiderstand vernachlässigt, entspricht der Beschleunigungswert der Schwerkraft: 9,8 m / s2.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill. 40-45.
- Figueroa, D. Physikreihe für Naturwissenschaften und Technik. Band 3 .. Auflage. Kinematik. 69-85.
- Giancoli, D. Physik: Prinzipien mit Anwendungen. 6th. Ed Prentice Hall. 19-36.
- Hewitt, Paul. 2012. Konzeptionelle Physik. 5th. Ed. Pearson. 14-18.
- Kirkpatrick, L. 2007. Physik: Ein Blick auf die Welt. 6ta Verkürzte Ausgabe. Lernen einbinden. 15-19.
- Wilson, J. 2011. Physik 10. Pearson Education. 116-119


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.