
Methode der kleinsten Quadrate, Übungen und wofür es ist
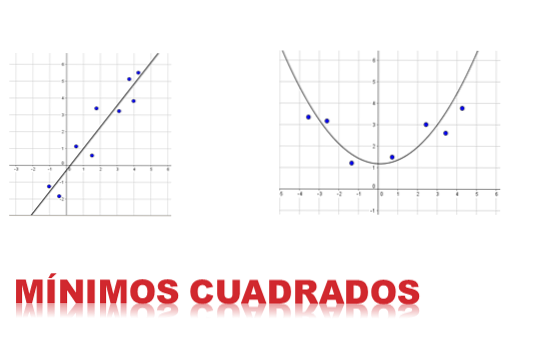
Die Methode von Kleinsten Quadrate Es ist eine der wichtigsten Anwendungen bei der Approximation von Funktionen. Die Idee ist, eine Kurve so zu finden, dass diese Funktion bei einem Satz geordneter Paare die Daten am besten approximiert. Die Funktion kann eine Linie, eine quadratische Kurve, eine kubische usw. sein..
Die Idee der Methode besteht darin, die Summe der Quadrate der Differenzen in der Ordinate (Y-Komponente) zwischen den von der gewählten Funktion erzeugten Punkten und den zum Datensatz gehörenden Punkten zu minimieren.
Artikelverzeichnis
- 1 Methode der kleinsten Quadrate
- 2 Gelöste Übungen
- 2.1 Übung 1
- 2.2 Übung 2
- 3 Wofür ist es??
- 4 Referenzen
Methode der kleinsten Quadrate
Bevor wir die Methode angeben, müssen wir uns zunächst darüber im Klaren sein, was „besserer Ansatz“ bedeutet. Angenommen, wir suchen nach einer Linie y = b + mx, die eine Menge von n Punkten am besten darstellt, nämlich (x1, y1), (x2, y2)…, (xn, yn).
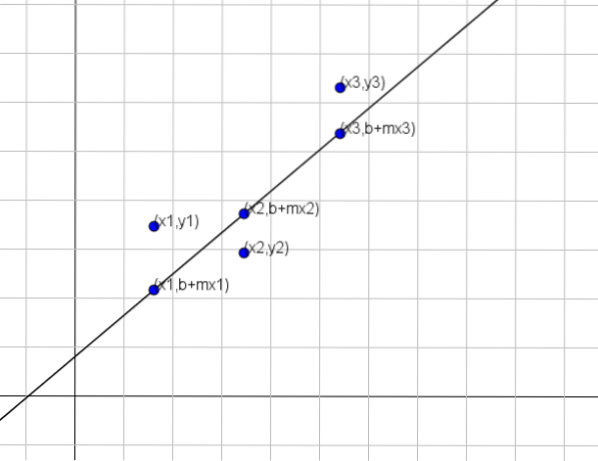
Wie in der vorherigen Abbildung gezeigt, wäre der entsprechende Wert von y für x = x1 b + mx1, wenn die Variablen x und y durch die Linie y = b + mx in Beziehung stehen würden. Dieser Wert unterscheidet sich jedoch von dem wahren Wert von y, der y = y1 ist.
Denken Sie daran, dass in der Ebene der Abstand zwischen zwei Punkten durch die folgende Formel angegeben wird:
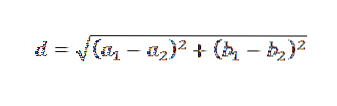
Vor diesem Hintergrund erscheint es logisch, die Auswahl der Linie als Kriterium zu verwenden, um die Summe der Quadrate der Abstände zwischen den zu minimieren, um die Art und Weise zu bestimmen, in der die Linie y = b + mx ausgewählt wird, die den gegebenen Daten am besten entspricht Punkte und die Gerade.
Da der Abstand zwischen den Punkten (x1, y1) und (x1, b + mx1) y1- (b + mx1) beträgt, reduziert sich unser Problem darauf, die Zahlen m und b so zu finden, dass die folgende Summe minimal ist:
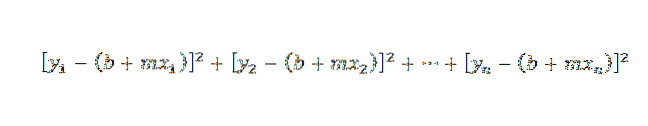
Die Linie, die diese Bedingung erfüllt, ist als "Annäherung der Linie der kleinsten Quadrate an die Punkte (x1, y1), (x2, y2), ..., (xn, yn)" bekannt..
Sobald das Problem gelöst ist, muss nur noch eine Methode ausgewählt werden, um die Approximation der kleinsten Quadrate zu finden. Wenn die Punkte (x1, y1), (x2, y2), ..., (xn, yn) alle auf der Linie y = mx + b liegen, hätten wir, dass sie kollinear y sind:
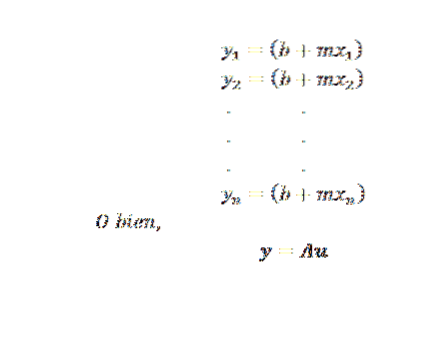
In diesem Ausdruck:
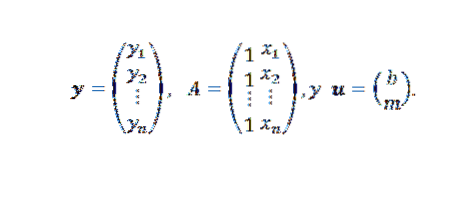
Wenn die Punkte nicht kollinear sind, ist y-Au = 0 und das Problem kann in das Finden eines Vektors u übersetzt werden, so dass die euklidische Norm minimal ist.
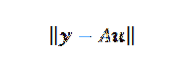
Das Finden des Minimierungsvektors u ist nicht so schwierig, wie Sie vielleicht denken. Da A eine nx2-Matrix und u eine 2 × 1-Matrix ist, haben wir, dass der Vektor Au ein Vektor in R istn y gehört zum Bild von A, das ein Unterraum von R istn mit einer Abmessung von nicht mehr als zwei.
Wir nehmen an, dass n = 3 ist, um zu zeigen, welche Prozedur zu befolgen ist. Wenn n = 3 ist, ist das Bild von A eine Ebene oder eine Linie, die durch den Ursprung verläuft.
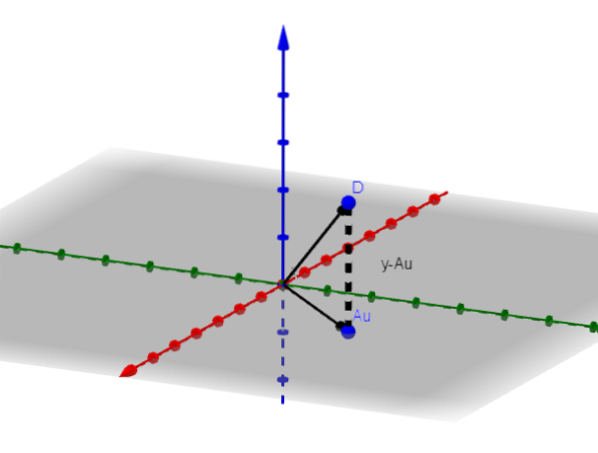
Sei v der Minimierungsvektor. In der Figur beobachten wir, dass y-Au minimiert wird, wenn es orthogonal zum Bild von A ist. Das heißt, wenn v der Minimierungsvektor ist, dann passiert es, dass:
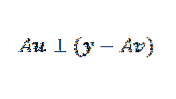
Dann können wir das Obige folgendermaßen ausdrücken:
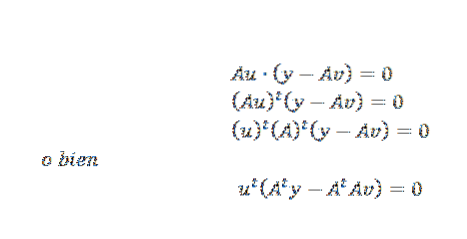
Dies kann nur passieren, wenn:
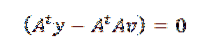
Wenn wir schließlich nach v auflösen, haben wir:
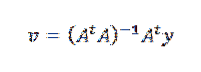
Dies ist möglich, da A.tA ist invertierbar, solange die als Daten angegebenen n Punkte nicht kollinear sind.
Wenn wir nun nach einer Linie suchen wollten, wollten wir eine Parabel finden (deren Ausdruck die Form y = a + bx + cx haben würdezwei) Dies wäre eine bessere Annäherung an die n Datenpunkte. Das Verfahren wäre wie nachstehend beschrieben.
Wenn die n Datenpunkte in dieser Parabel wären, hätten wir:
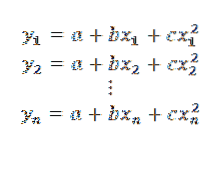
Später:
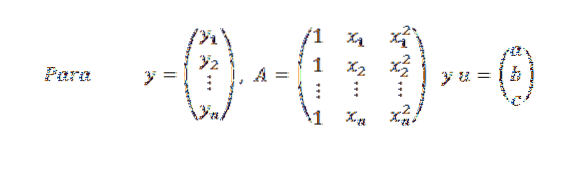
Ebenso können wir y = Au schreiben. Wenn nicht alle Punkte in der Parabel sind, haben wir, dass y-Au für jeden Vektor u von Null verschieden ist, und unser Problem ist wieder: Finden Sie einen Vektor u in R3 so, dass seine Norm || y-Au || sei so klein wie möglich.
Wenn wir das vorherige Verfahren wiederholen, können wir feststellen, dass der gesuchte Vektor ist:
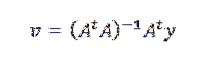
Gelöste Übungen
Übung 1
Finden Sie die Linie, die am besten zu den Punkten (1,4), (-2,5), (3, -1) und (4,1) passt..
Lösung
Wir müssen:
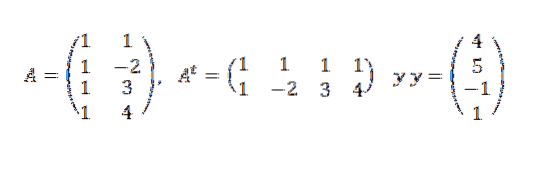
Später:
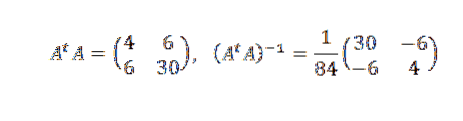
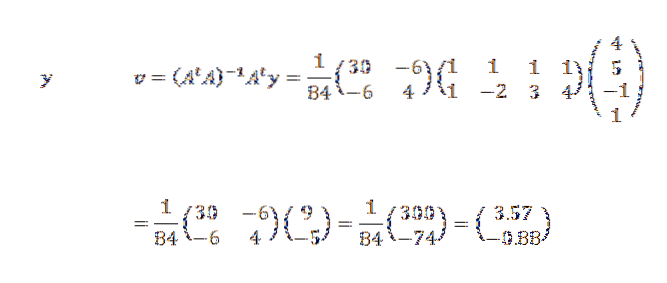
Daher schließen wir, dass die Linie, die am besten zu den Punkten passt, gegeben ist durch:
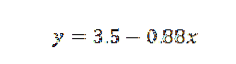
Übung 2
Angenommen, ein Objekt wird aus einer Höhe von 200 m fallen gelassen. Beim Fallen werden die folgenden Schritte unternommen:
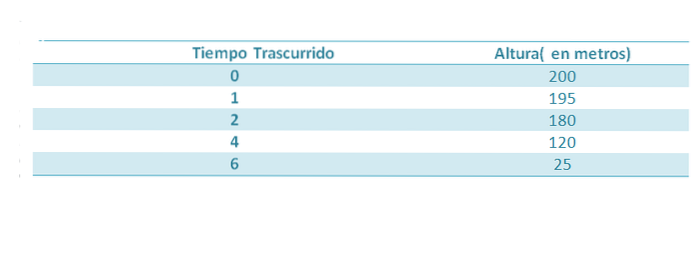
Wir wissen, dass die Höhe des Objekts nach Ablauf einer Zeit t gegeben ist durch:
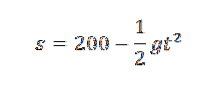
Wenn wir den Wert von g erhalten wollen, können wir nach einer Parabel suchen, die eine bessere Annäherung an die fünf in der Tabelle angegebenen Punkte darstellt, und daher hätten wir den Koeffizienten, der t begleitetzwei wird eine vernünftige Annäherung an (-1/2) g sein, wenn die Messungen genau sind.
Wir müssen:
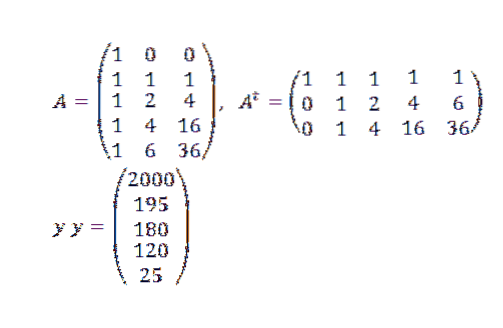
Und später:
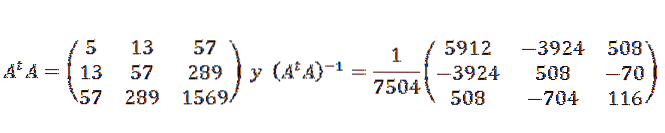

Die Datenpunkte werden also durch den folgenden quadratischen Ausdruck angepasst:
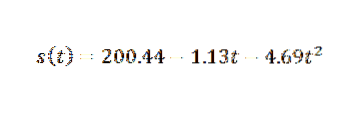
Also musst du:
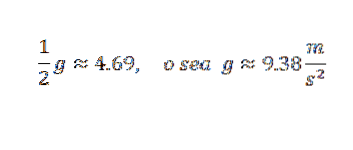
Dies ist ein Wert, der ziemlich nahe an der Korrektur liegt, nämlich g = 9,81 m / szwei. Um eine genauere Annäherung von g zu erhalten, wäre es notwendig, von genaueren Beobachtungen auszugehen.
Wofür ist das?
Bei den Problemen, die in den Natur- oder Sozialwissenschaften auftreten, ist es zweckmäßig, die Beziehungen, die zwischen verschiedenen Variablen bestehen, mit Hilfe eines mathematischen Ausdrucks zu schreiben.
In der Wirtschaft können wir beispielsweise Kosten (C), Einkommen (I) und Gewinne (U) mit einer einfachen Formel in Beziehung setzen:
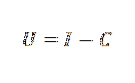
In der Physik können wir die durch die Schwerkraft verursachte Beschleunigung, die Zeit, in der ein Objekt gefallen ist, und die Höhe des Objekts per Gesetz in Beziehung setzen:
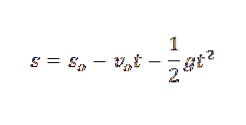
Im vorherigen Ausdruck soder ist die Anfangshöhe des Objekts und voder ist seine Anfangsgeschwindigkeit.
Solche Formeln zu finden ist jedoch keine leichte Aufgabe; In der Regel ist es Sache des diensthabenden Fachmanns, mit vielen Daten zu arbeiten und wiederholt mehrere Experimente durchzuführen (um zu überprüfen, ob die erzielten Ergebnisse konstant sind), um Beziehungen zwischen den verschiedenen Daten zu finden.
Ein üblicher Weg, dies zu erreichen, besteht darin, die in einer Ebene erhaltenen Daten als Punkte darzustellen und nach einer stetigen Funktion zu suchen, die diese Punkte optimal approximiert..
Eine der Möglichkeiten, die Funktion zu finden, die die angegebenen Daten "am besten approximiert", ist die Methode der kleinsten Quadrate..
Wie wir auch in der Übung gesehen haben, können wir dank dieser Methode ziemlich genaue Annäherungen an physikalische Konstanten erhalten.
Verweise
- Charles W Curtis Lineare Algebra. Springer-Velarg
- Kai Lai Chung. Elementare Proability-Theorie mit stochastischen Prozessen. Springer-Verlag New York Inc.
- Richar L Burden & J. Douglas Faires. Numerische Analyse (7ed). Thompson Lernen.
- Stanley I. Grossman. Anwendungen der linearen Algebra. MCGRAW-HILL / INTERAMERICANA DE MEXICO
- Stanley I. Grossman. Lineare Algebra. MCGRAW-HILL / INTERAMERICANA DE MEXICO



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.